Содержание
- 2. Основы логики Знание символики Знание таблиц истинности основных логических операций (инверсия, конъюнкция, дизъюнкция), а также импликации
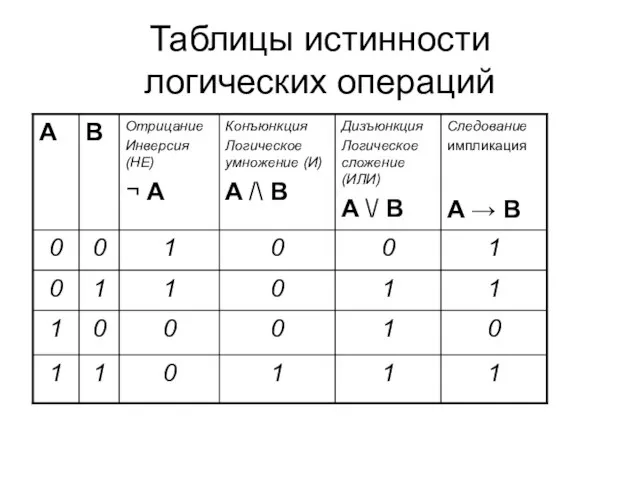
- 3. Таблицы истинности логических операций
- 4. Основы логики Пример 1. Для какого из указанных значений X истинно высказывание ¬ ((X >2) →
- 5. Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/ ¬ B \/ C) 1) ¬A
- 6. Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/ ¬ B \/ C) 1) ¬A
- 7. Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/ ¬ B \/ C) 1) ¬A
- 8. Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/ ¬ B \/ C) 1) ¬A
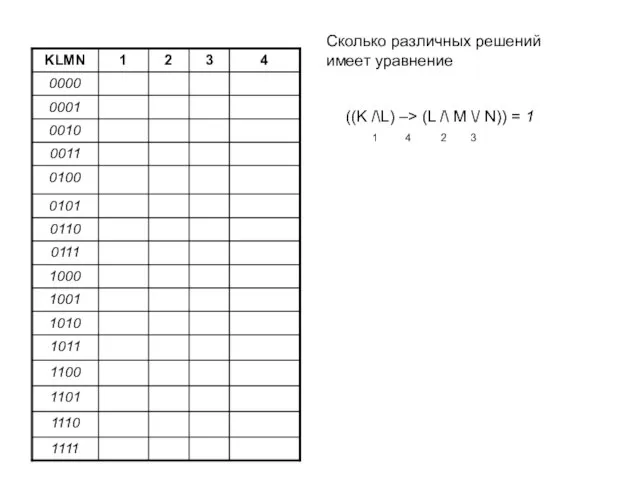
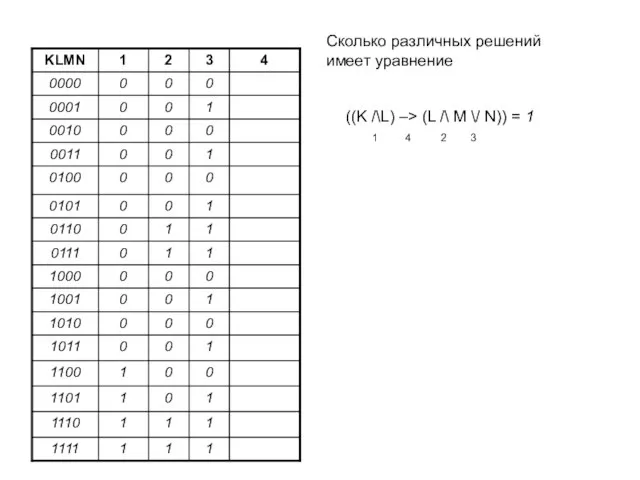
- 9. Пример 3. Сколько различных решений имеет уравнение ((K /\L) –> (L /\ M \/ N)) =
- 10. ((K /\L) –> (L /\ M \/ N)) = 1 1 4 2 3 Сколько различных
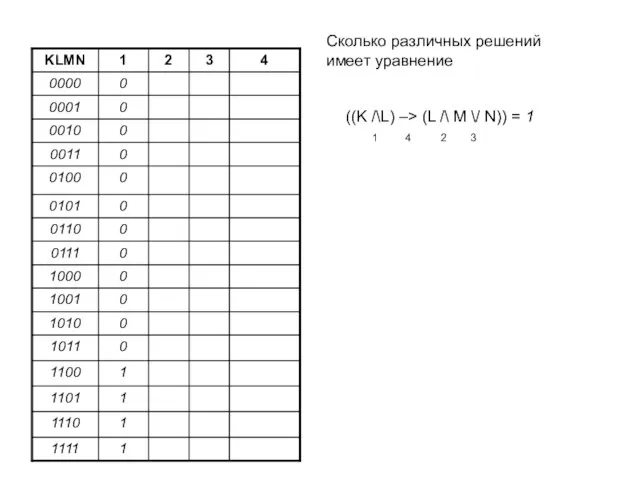
- 11. ((K /\L) –> (L /\ M \/ N)) = 1 1 4 2 3 Сколько различных
- 12. ((K /\L) –> (L /\ M \/ N)) = 1 1 4 2 3 Сколько различных
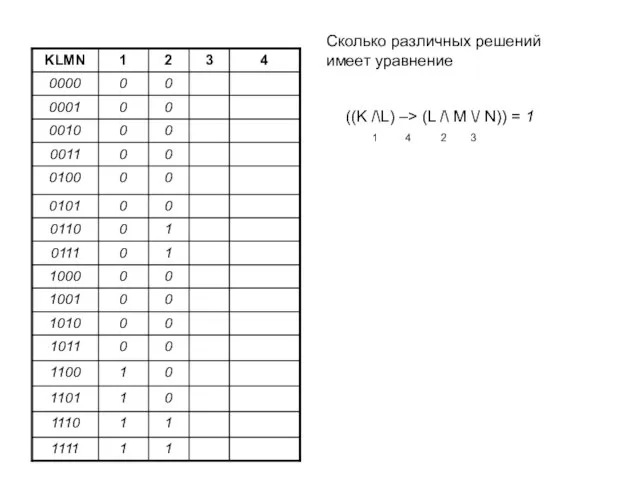
- 13. ((K /\L) –> (L /\ M \/ N)) = 1 1 4 2 3 Сколько различных
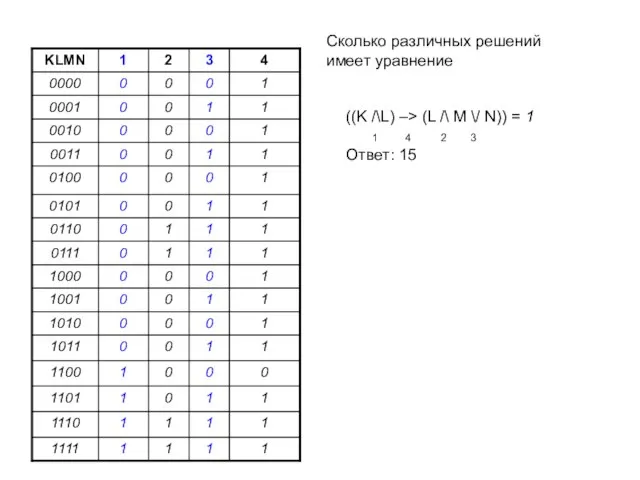
- 14. ((K /\L) –> (L /\ M \/ N)) = 1 1 4 2 3 Ответ: 15
- 15. Пример 4. Для какого из указанных значений X истинно высказывание ¬ ((X>2) → (X>3))? 1)x=1 2)
- 16. Пример 4. Для какого из указанных значений X истинно высказывание ¬ ((X>2) → (X>3))? 1)x=1 2)
- 17. Пример 4. Для какого из указанных значений X истинно высказывание ¬ ((X>2) → (X>3))? 1)x=1 2)
- 18. Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) → (X>3))?
- 19. Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) → (X>3))? Решение: ¬ ((X>2) →
- 20. Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) → (X>3))? Решение: ¬ ((X>2) →
- 21. Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) → (X>3))? Решение: ¬ ((X>2) →
- 22. Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) → (X>3))? Решение: ¬ ((X>2) →
- 23. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90
- 24. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90 Решение: (90
- 25. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90 Решение: (90 Из таблицы истинности
- 26. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90 Решение: (90 Из таблицы истинности
- 27. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90 Решение: (90 Из таблицы истинности
- 28. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90 Решение: (90 Из таблицы истинности
- 29. Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно (90 Решение: (90 Из таблицы истинности
- 30. Пример 7. Каково наибольшее целое число X, при котором истинно высказывание (50 (X+1)·(X+1)) Решение: (50 (X+1)2)
- 31. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 (X2>50) = 0
- 32. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 33. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 34. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 35. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 36. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 37. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 38. Решение: (50 (X+1)2) = 1 Из таблицы истинности импликации (X2>50) = 1 (X+1)2 x √50 -√50
- 39. Проверка. (50 (X+1)2) при x= 7 (50 (7+1)2) (50 64) истина при x= -8 (50 (-8+1)2)
- 40. Пример 8. Пончик, Ленчик и Батончик нашли клад. Один из них этот клад утаил. На следствии
- 41. Простые высказывания П – Пончик утаил клад Л - Ленчик утаил клад Б - Батончик утаил
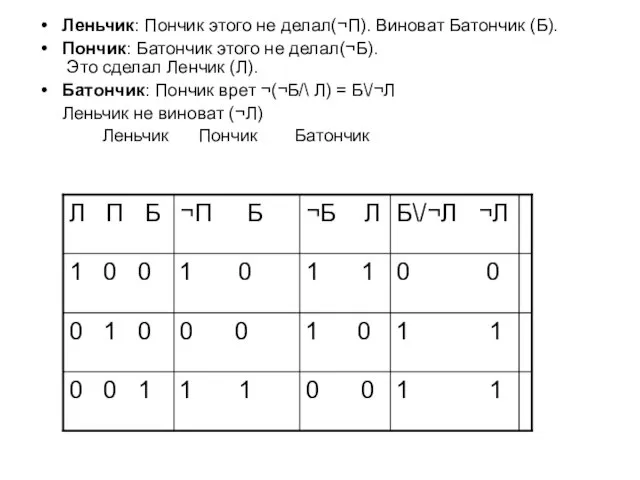
- 42. Леньчик: Пончик этого не делал(¬П). Виноват Батончик (Б). Пончик: Батончик этого не делал(¬Б). Это сделал Ленчик
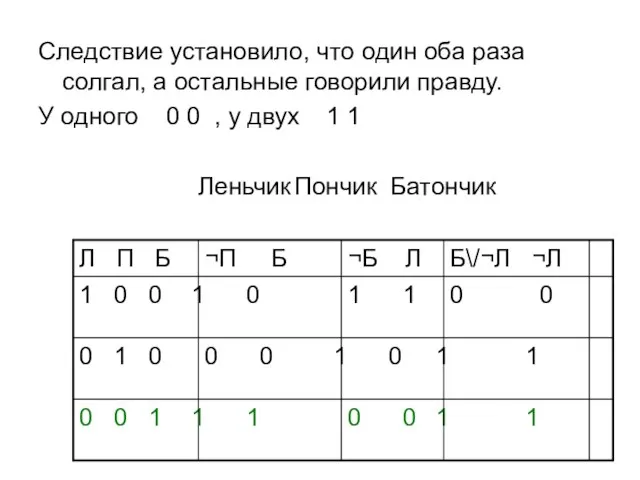
- 43. Следствие установило, что один оба раза солгал, а остальные говорили правду. У одного 0 0 ,
- 44. Пример 9. Синоптик объявляет погоду на завтра и утверждает следующее: Если не будет ветра, то будет
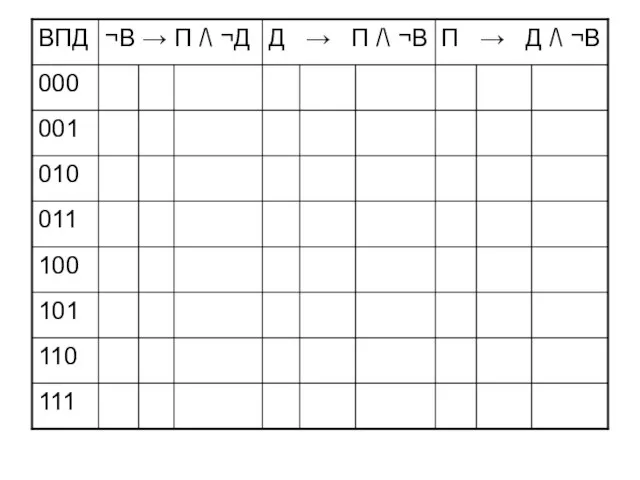
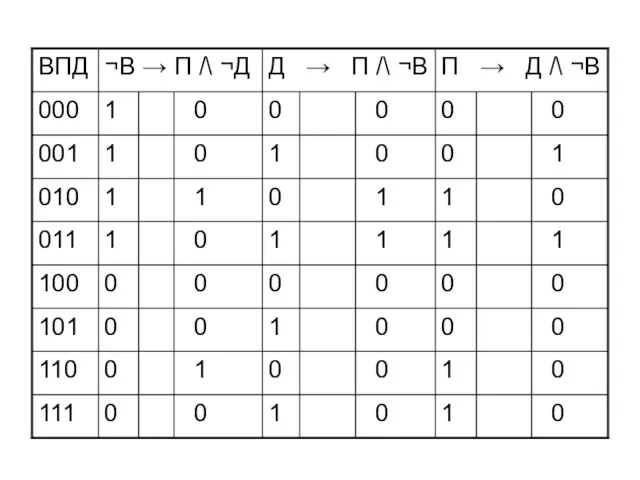
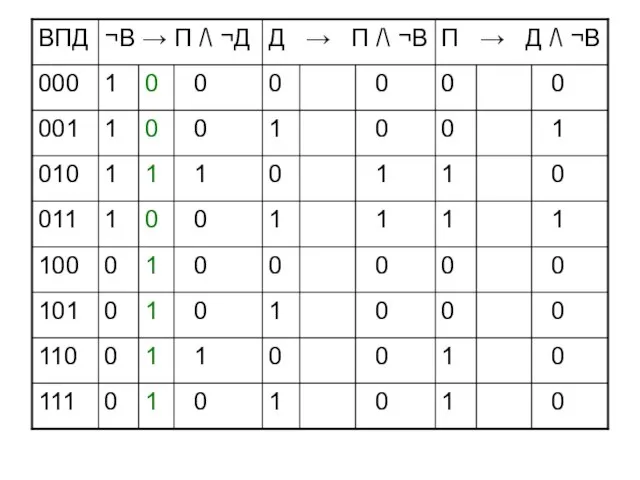
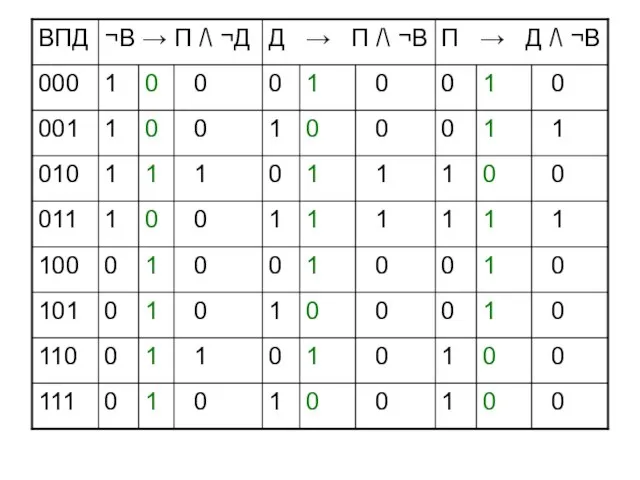
- 45. Запишем высказывания Если не будет ветра, то будет пасмурная погода без дождя ¬В → П /\
- 46. Запишем высказывания Если не будет ветра, то будет пасмурная погода без дождя ¬В → П /\
- 47. Запишем высказывания Если не будет ветра, то будет пасмурная погода без дождя ¬В → П /\
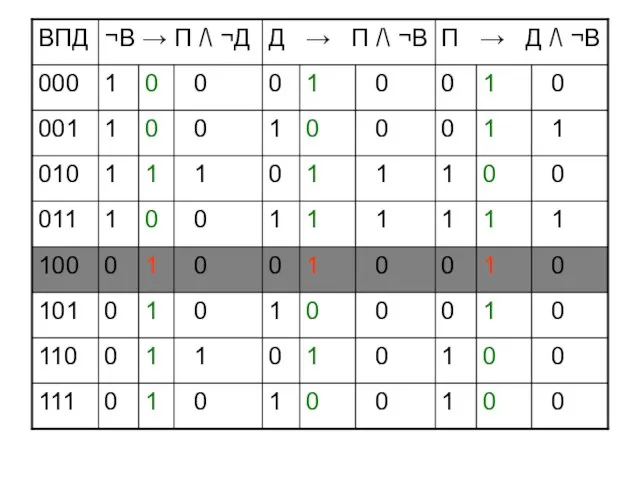
- 53. Простые высказывания В – ветер П – пасмурно Д - дождь В – 1 П –
- 54. Пример 10.
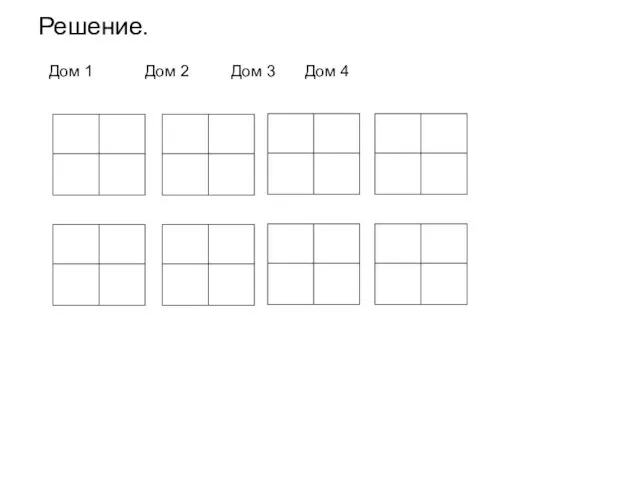
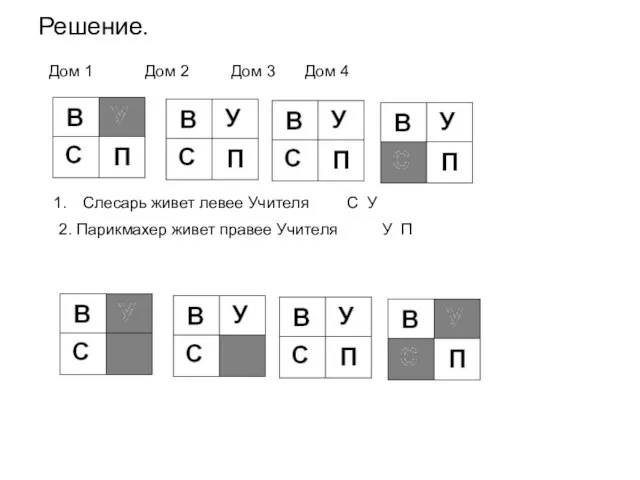
- 55. Решение. Дом 1 Дом 2 Дом 3 Дом 4
- 56. Решение. Слесарь живет левее Учителя С У 2. Парикмахер живет правее Учителя У П 3. Врач
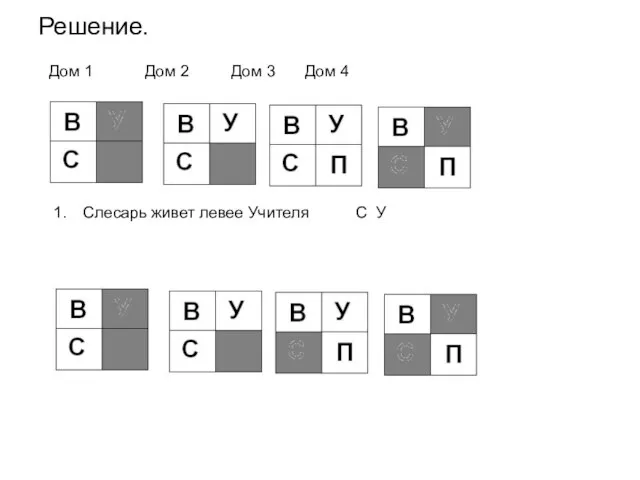
- 57. Решение. Дом 1 Дом 2 Дом 3 Дом 4 Слесарь живет левее Учителя С У 2.
- 58. Решение. Дом 1 Дом 2 Дом 3 Дом 4 Слесарь живет левее Учителя С У
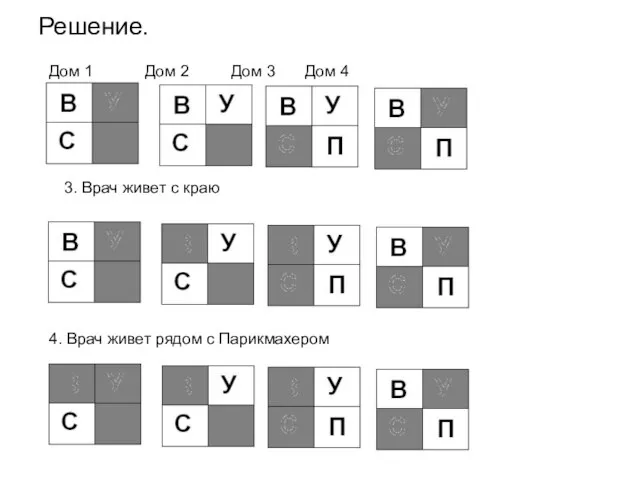
- 59. Решение. Дом 1 Дом 2 Дом 3 Дом 4 4. Врач живет рядом с Парикмахером 3.
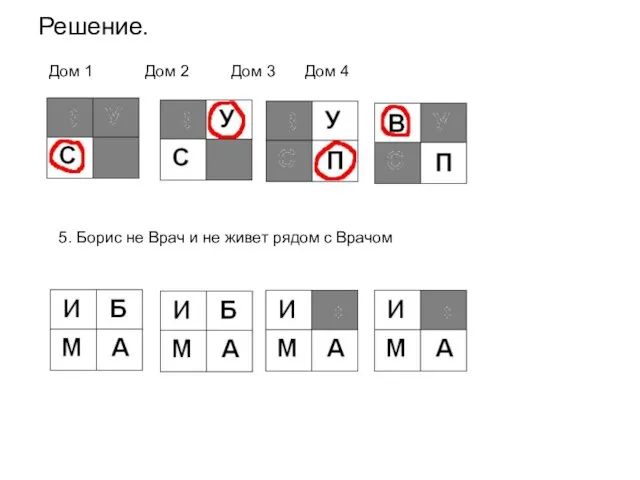
- 60. Решение. Дом 1 Дом 2 Дом 3 Дом 4 5. Борис не Врач и не живет
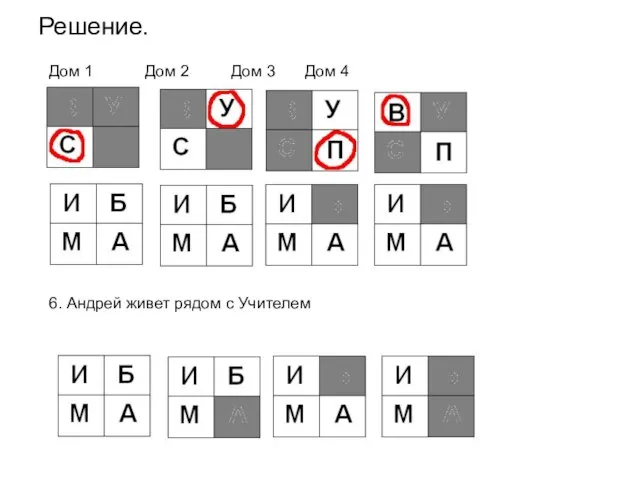
- 61. Решение. Дом 1 Дом 2 Дом 3 Дом 4 6. Андрей живет рядом с Учителем
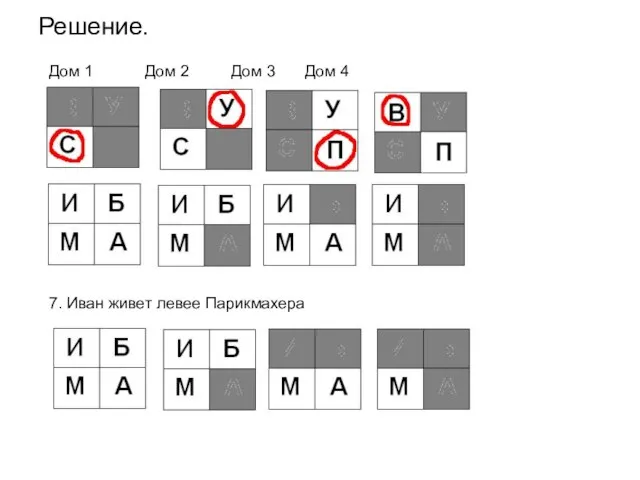
- 62. Решение. Дом 1 Дом 2 Дом 3 Дом 4 7. Иван живет левее Парикмахера
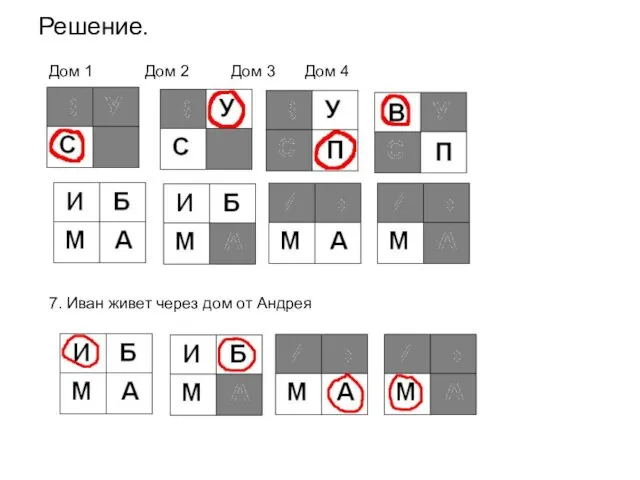
- 63. Решение. Дом 1 Дом 2 Дом 3 Дом 4 7. Иван живет через дом от Андрея
- 65. Скачать презентацию



























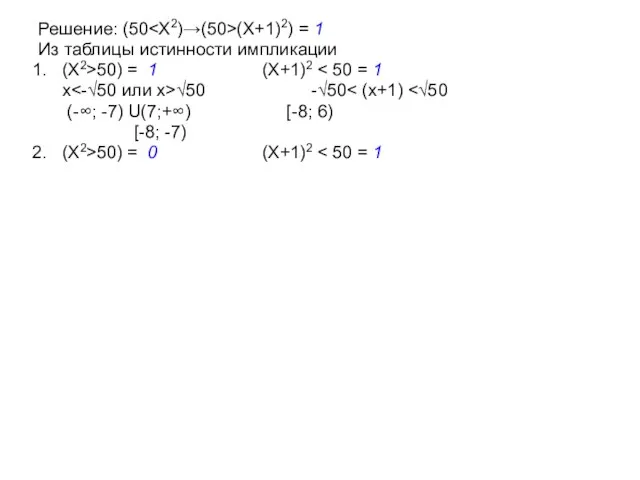

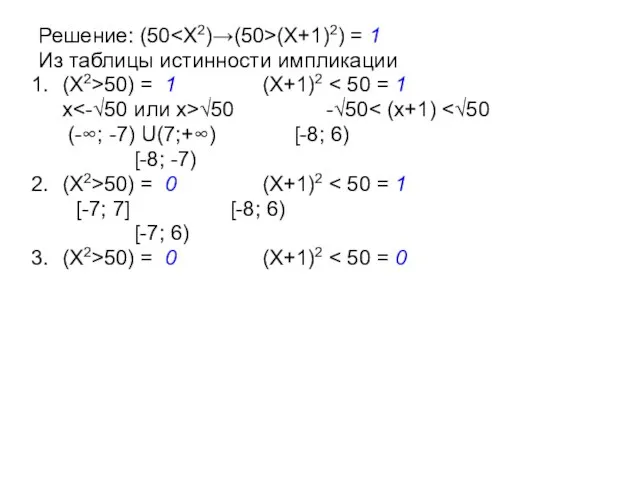











 Председательствование Украины в Комитете Министров Совета Европы Приоритет «Защита прав ребенка» Мероприятие для стран-члено
Председательствование Украины в Комитете Министров Совета Европы Приоритет «Защита прав ребенка» Мероприятие для стран-члено Святые страстотерпцы князья Борис и Глеб
Святые страстотерпцы князья Борис и Глеб Российский канцелярский форум
Российский канцелярский форум Одноклітинні організми. Явище колоніальності
Одноклітинні організми. Явище колоніальності Национальная политика в правление Александра I и Николая I
Национальная политика в правление Александра I и Николая I Инновационные технологии диагностики и мониторинга плоских кровель
Инновационные технологии диагностики и мониторинга плоских кровель Создание школьной экологической газеты «Nature»
Создание школьной экологической газеты «Nature» Деление и устный счет
Деление и устный счет Информационное общество. Защита информации
Информационное общество. Защита информации Биография Короленко
Биография Короленко Органы прокуратуры Российской Федерации. Тема 7
Органы прокуратуры Российской Федерации. Тема 7 Крутятся диски
Крутятся диски Леса России
Леса России Программа Bachelor of Business Administration (ВВА)
Программа Bachelor of Business Administration (ВВА) ПОБЕДИТЕЛИ ПЕРВОГО ОБЛАСТНОГО КОНКУРСА МОЛОДЕЖНЫХ ИНТЕРНЕТ-ПРОЕКТОВ «ЗОЛОТАЯ ПАУТИНА»
ПОБЕДИТЕЛИ ПЕРВОГО ОБЛАСТНОГО КОНКУРСА МОЛОДЕЖНЫХ ИНТЕРНЕТ-ПРОЕКТОВ «ЗОЛОТАЯ ПАУТИНА» Мы вместе. Международная премия
Мы вместе. Международная премия О жизни и творчестве С.А. Есенина
О жизни и творчестве С.А. Есенина Шаблон курсовой работы
Шаблон курсовой работы Водные ресурсы Марса
Водные ресурсы Марса Презентация на тему Былины
Презентация на тему Былины Вице-президент Российской академии образования, академик А. А. Кузнецов Главный научный сотрудник Института проблем информатики Р
Вице-президент Российской академии образования, академик А. А. Кузнецов Главный научный сотрудник Института проблем информатики Р Инструкция по регистрации и верификации Служб для продавцов и Сервиса платежей
Инструкция по регистрации и верификации Служб для продавцов и Сервиса платежей Евтушенко Евгений Александрович
Евтушенко Евгений Александрович Админ
Админ Презентация для родителей
Презентация для родителей Архітектура ПЛК Mitsubishi FX3U
Архітектура ПЛК Mitsubishi FX3U Арабы
Арабы Бизнес-планирование. Курс лекций
Бизнес-планирование. Курс лекций