Содержание
- 2. Этапы выполнения квантово-химического исследования постановка задачи исследования механизма реакции, куда входит поиск литературы по заданной тематике,
- 3. Полная информация о механизме реакции должна включать установление последовательности элементарных стадий, а также данные о структуре
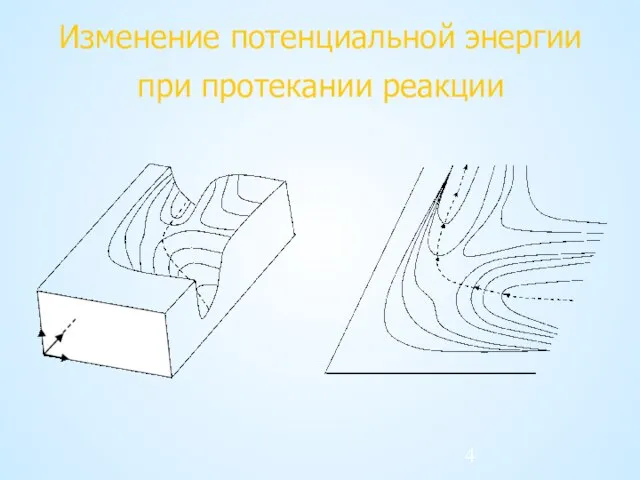
- 4. Изменение потенциальной энергии при протекании реакции
- 5. Для любой критической точки поверхности потенциальной энергии значение производных (градиент) по каждой независимой координате ядер qi
- 6. Поиск переходных состояний на поверхности потенциальной энергии Если силовые константы нормальных колебаний системы имеют одно отрицательное
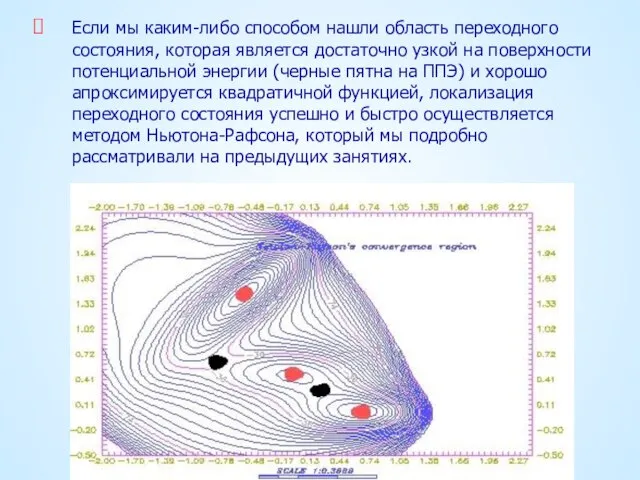
- 7. Если мы каким-либо способом нашли область переходного состояния, которая является достаточно узкой на поверхности потенциальной энергии
- 8. Также как и для оптимизации структур минимумов, поиск переходных состояний представляет собой итерационную процедуру, продолжающуюся до
- 9. Критерии сходимости в Gaussian В программе GAUSSIAN используются следующие критерии сходимости (КС) (приведены значения, используемые по
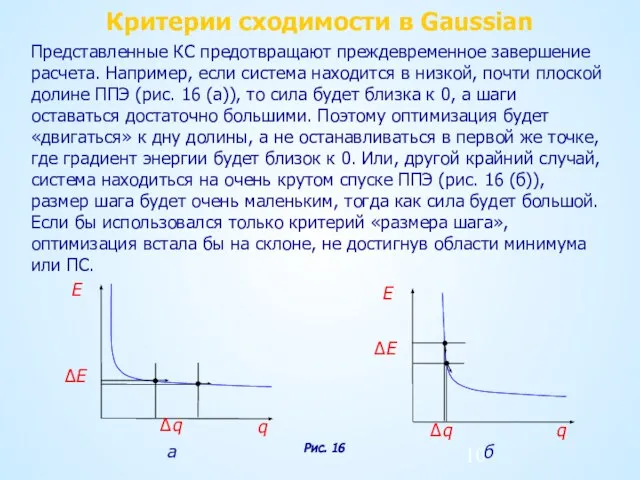
- 10. Критерии сходимости в Gaussian Представленные КС предотвращают преждевременное завершение расчета. Например, если система находится в низкой,
- 11. Методы поиска переходных состояний Методы линейного и квадратичного транзита. Метод «реакционной координаты». Методы прямого поиска переходного
- 12. Методы линейного транзита. Машина автоматически сама создает исходную структуру для расчета переходного состояния по заданным структурам
- 13. Методы квадратичного транзита. Методы квадратичного транзита подразделяются на два типа. Основаны на методе линейного транзита, т.е.
- 14. Методы квадратичного транзита. Методы квадратичного транзита подразделяются на два типа. 2. Находят максимум в сечении поверхности
- 15. Методы квадратичного транзита. Недостатком этих методов является то, что если поверхность сильно искривлена, то структура ПС
- 16. Метод «реакционной координаты». Выделяют одну из координат qi системы, обычно претерпевающую наиболее существенные изменения в ходе
- 17. Прямой поиск переходного состояния Этот способ требует задания исходной структуры переходного состояния самостоятельно, например, на основании
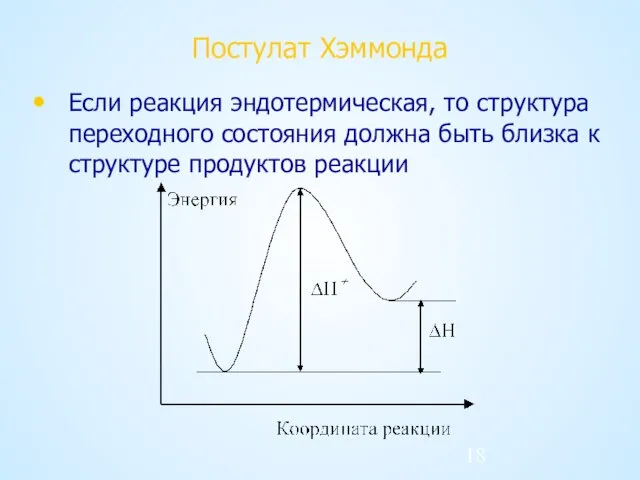
- 18. Постулат Хэммонда Если реакция эндотермическая, то структура переходного состояния должна быть близка к структуре продуктов реакции
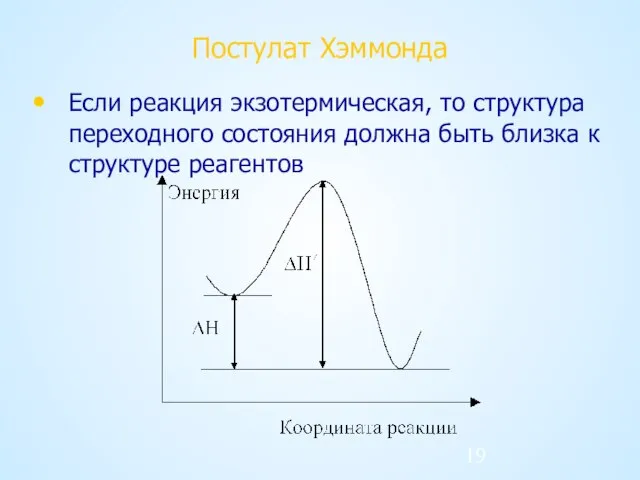
- 19. Постулат Хэммонда Если реакция экзотермическая, то структура переходного состояния должна быть близка к структуре реагентов
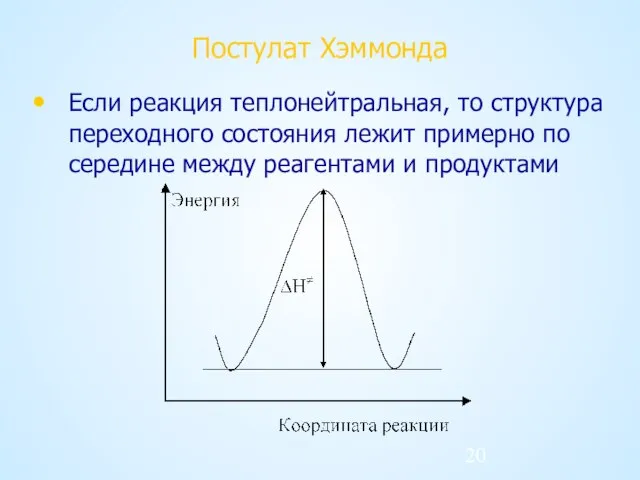
- 20. Постулат Хэммонда Если реакция теплонейтральная, то структура переходного состояния лежит примерно по середине между реагентами и
- 21. Прямой поиск переходного состояния Рекомендуется добавить еще один из двух параметров – EF или GDIIS: EF
- 22. Поиск переходных состояний методом квадратичного транзита QST2 в Gaussian Для поиска переходных состояний методом квадратичного транзита
- 23. Поиск переходных состояний методом квадратичного транзита QST2 в Gaussian Разделы спецификаций молекул, как и в случае
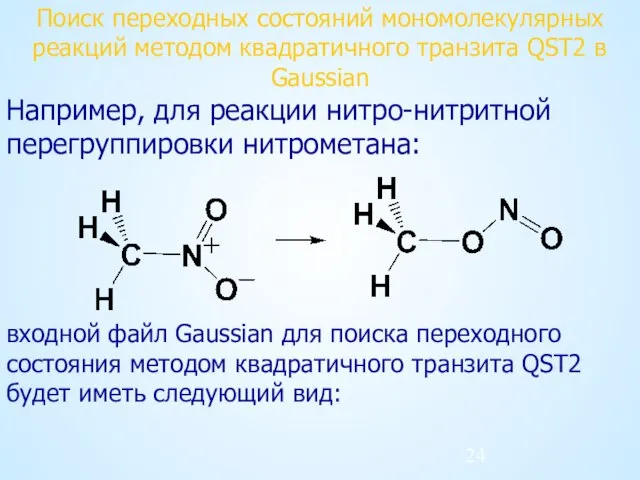
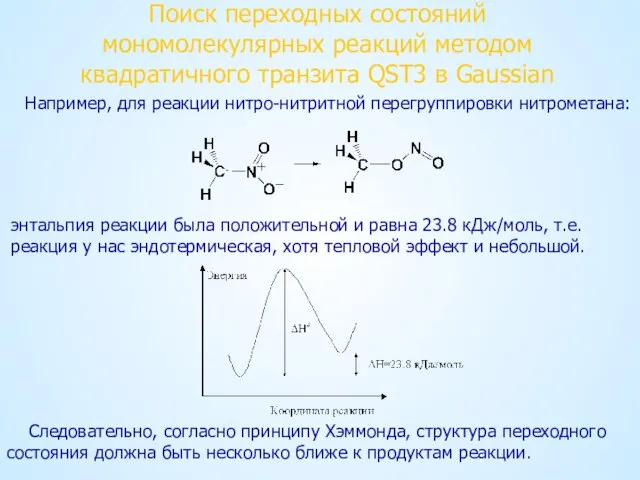
- 24. Поиск переходных состояний мономолекулярных реакций методом квадратичного транзита QST2 в Gaussian Например, для реакции нитро-нитритной перегруппировки
- 25. Входной файл Gaussian для поиска переходного состояния мономолекулярных реакций методом квадратичного транзита QST2 в декартовых координатах
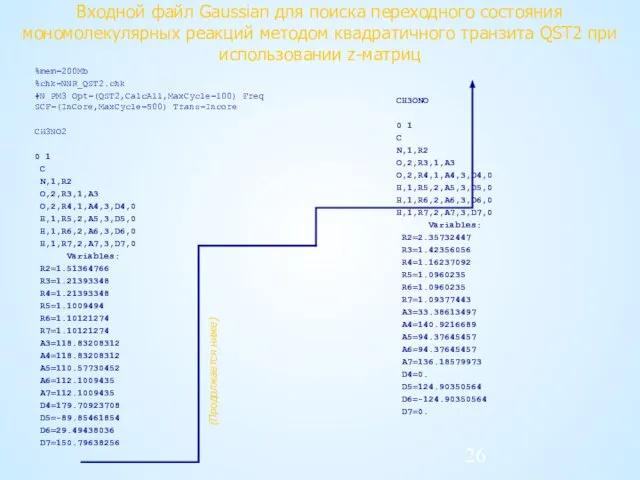
- 26. Входной файл Gaussian для поиска переходного состояния мономолекулярных реакций методом квадратичного транзита QST2 при использовании z-матриц
- 27. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 28. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
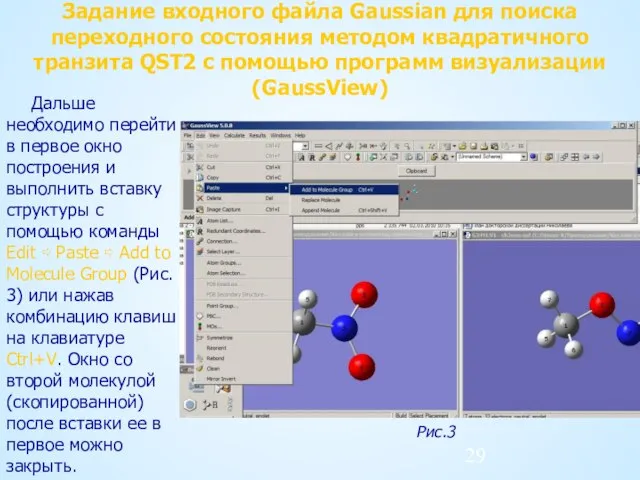
- 29. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 30. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 31. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 32. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 33. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
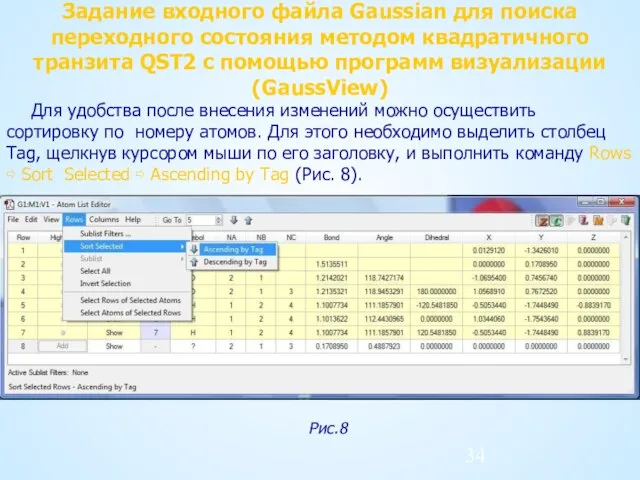
- 34. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
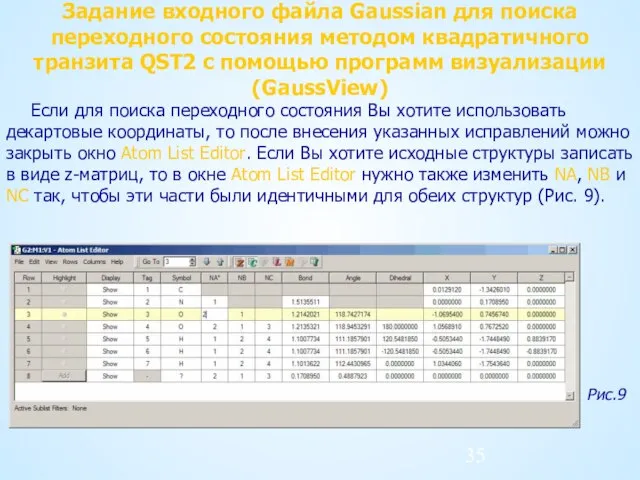
- 35. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
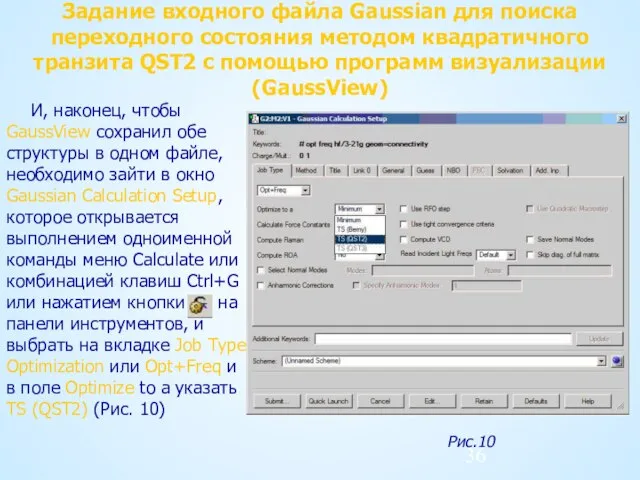
- 36. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 37. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 38. Поиск переходных состояний методом квадратичного транзита QST2 в Gaussian В случае, когда метод QST2 не может
- 39. Поиск переходных состояний методом квадратичного транзита QST3 в Gaussian Для поиска переходных состояний методом квадратичного транзита
- 40. Поиск переходных состояний методом квадратичного транзита QST3 в Gaussian Разделы спецификаций молекул, как и в случае
- 41. Поиск переходных состояний мономолекулярных реакций методом квадратичного транзита QST3 в Gaussian Например, для реакции нитро-нитритной перегруппировки
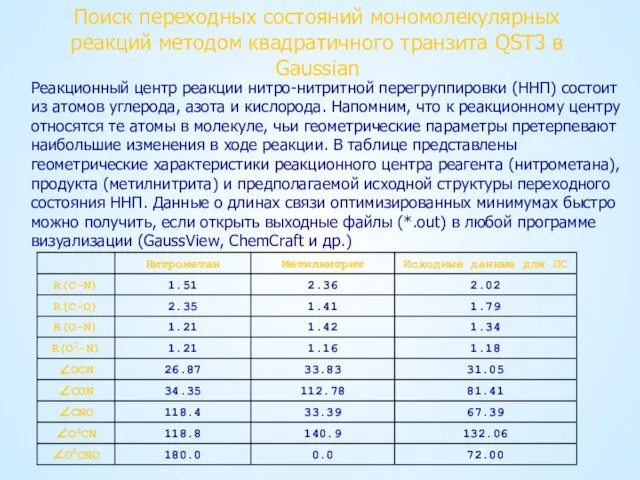
- 42. Поиск переходных состояний мономолекулярных реакций методом квадратичного транзита QST3 в Gaussian Реакционный центр реакции нитро-нитритной перегруппировки
- 43. Входной файл Gaussian для поиска переходного состояния мономолекулярных реакций методом квадратичного транзита QST3 при использовании z-матриц
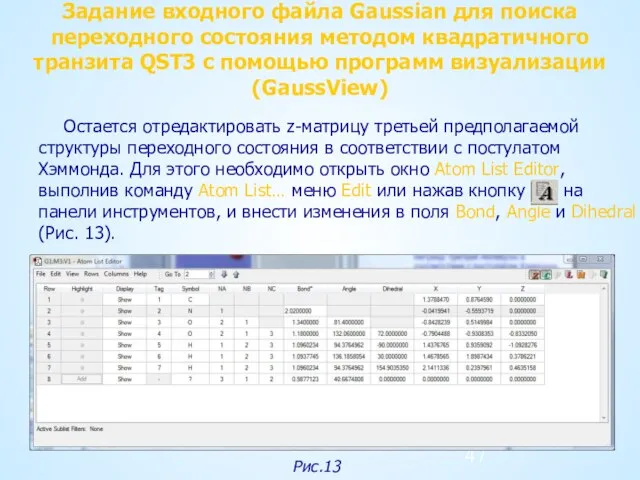
- 44. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST3 с помощью программ визуализации
- 45. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST3 с помощью программ визуализации
- 46. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST3 с помощью программ визуализации
- 47. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST3 с помощью программ визуализации
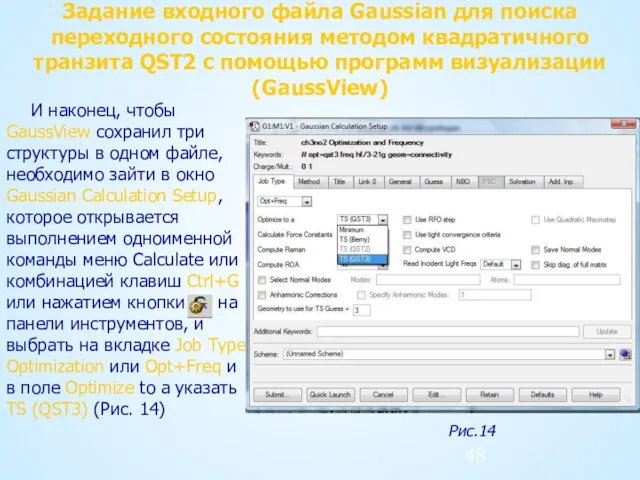
- 48. Задание входного файла Gaussian для поиска переходного состояния методом квадратичного транзита QST2 с помощью программ визуализации
- 49. Входной файл Gaussian для прямого поиска переходного состояния мономолекулярных реакций при использовании z-матриц %mem=200Mb %chk=NNR_TS.chk #N
- 50. Поиск переходных состояний бимолекулярной реакции Пусть у нас протекает следующая реакция: CH2O + •OH → H2O
- 51. Поиск переходных состояний бимолекулярной реакции Из этих данных нетрудно сосчитать энтальпию реакции образования воды из формальдегида
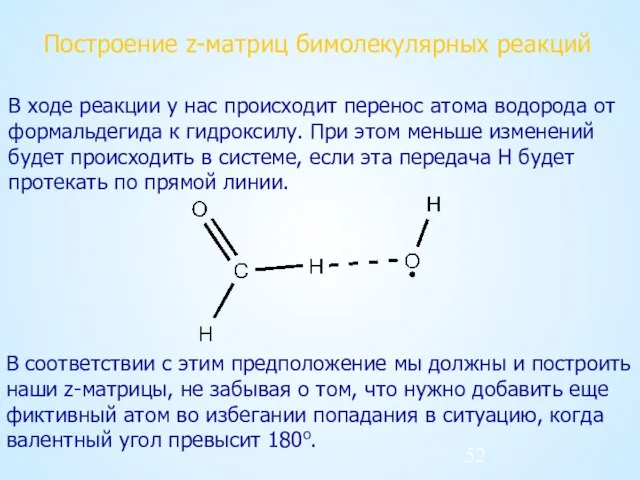
- 52. Построение z-матриц бимолекулярных реакций В ходе реакции у нас происходит перенос атома водорода от формальдегида к
- 53. Построение z-матриц бимолекулярных реакций Пронумеруем атомы в нашем комплексе. Заметим, что нумерация атомов выбрана таким образом,
- 54. Построение z-матриц бимолекулярных реакций Далее мы достраиваем эту z-матрицу – добавляем фиктивный атом X и атомы
- 55. Построение z-матриц бимолекулярных реакций C H,1,R2 H,1,R3,2,A3 O,1,R4,3,A4,2,D4,0 X,2,R5,1,A5,3,D5,0 O,2,R6,5,A6,1,D6,0 H,6,R7,2,A7,5,D7,0 Variables: R2=1.09125945 R3=1.09125837 R4=1.20218175 R6=3.0
- 56. Построение z-матриц бимолекулярных реакций Для комплекса продуктов реакции образования воды из формальдегида и гидроксила символьная z-матрица
- 57. Построение z-матриц бимолекулярных реакций C H,1,R2 H,1,R3,2,A3 O,1,R4,3,A4,2,D4,0 X,2,R5,1,A5,3,D5,0 O,2,R6,5,A6,1,D6,0 H,6,R7,2,A7,5,D7,0 Variables: R2=3.0 R3=1.0885455 R4=1.16587264 R6=0.95095252
- 58. Поиск переходного состояния бимолекулярных реакций методом квадратичного транзита QST2 в Gaussian %mem=200Mb %chk=Ch2O+OH_qst2.chk # uPM3 Opt=(qst2,Calcall,MaxCycle=100)
- 59. Поиск переходного состояния бимолекулярных реакций методом квадратичного транзита QST3 в Gaussian %mem=200Mb %chk=Ch2O+OH_qst2.chk # uPM3 Opt=(qst3,Calcall,MaxCycle=100)
- 60. Прямой поиск переходного состояния бимолекулярных реакций в Gaussian %mem=200Mb %chk=Ch2O+OH_ts.chk # uPM3 Opt=(ts,ef,Calcall,MaxCycle=100) Freq SCF=(InCore,MaxCycle=500) NoSymm
- 61. Анализ результатов поиска переходных состояний. Как и в случае минимизации, при поиске переходных состояний любым из
- 62. Анализ результатов поиска переходных состояний. Кроме того, для QST2 и QST3 Gaussian выдает информацию обо всех
- 63. Анализ результатов поиска переходных состояний. На начальной и конечной итерациях оптимизации Gaussian выдает дополнительную информацию о
- 64. Анализ данных, полученных в результате поиска переходного состояния реакции нитро-нитритной перегруппировки методом квадратичной сходимости QST2. В
- 65. Анализ данных, полученных в результате поиска переходного состояния реакции нитро-нитритной перегруппировки методом квадратичной сходимости QST2. Как
- 66. Анализ данных, полученных в результате поиска переходного состояния реакции нитро-нитритной перегруппировки методом квадратичной сходимости QST2. Тем
- 67. Анализ данных, полученных в результате поиска переходного состояния реакции нитро-нитритной перегруппировки методом квадратичной сходимости QST3. В
- 68. Анализ данных, полученных в результате поиска переходного состояния реакции нитро-нитритной перегруппировки методом квадратичной сходимости QST3. Как
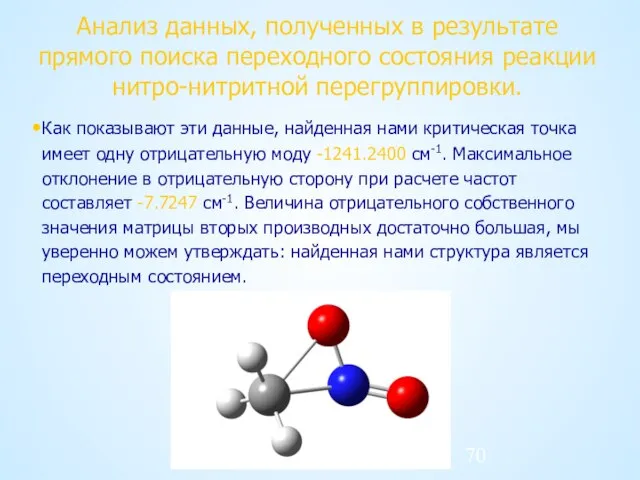
- 69. Анализ данных, полученных в результате прямого поиска переходного состояния реакции нитро-нитритной перегруппировки. В результате вычисления частот
- 70. Анализ данных, полученных в результате прямого поиска переходного состояния реакции нитро-нитритной перегруппировки. Как показывают эти данные,
- 71. Анализ данных, полученных в результате поиска переходного состояния реакции образования воды из формальдегида и гидроксила. Проанализировав
- 72. Доказательство принадлежности переходного состояния исследуемому процессу После локализации и идентификации переходных состояний обязательно необходимо доказать принадлежность
- 73. Этапы выполнения квантово-химического исследования постановка задачи исследования механизма реакции, куда входит поиск литературы по заданной тематике,
- 74. Путь химической реакции Наиболее распространено определение понятия пути химической реакции как линии минимальной энергии, связывающей соседние
- 75. Путь химической реакции При этом, поскольку E = E (q1,q2,q3,…,q3N-6) по построению есть такая поверхность потенциальной
- 76. Ключевые слова для спусков по пути реакции из переходного состояния к реагентам и продуктам Спуск по
- 77. Параметры ключевого слова IRC 1. Параметры, относящиеся к заданию силовых констант или начальных значений Гессиана: CalcFC
- 78. Параметры ключевого слова IRC 2. Параметры, управляющие количеством итераций, шагом движения по поверхности потенциальной энергии, а
- 79. Параметры ключевого слова IRC 3. Параметры, управляющие направлением движения по пути реакции (если они отсутствует, Gaussian
- 80. Параметры ключевого слова IRC 4. Если задача остановилась, например, из-за зацикливания оптимизации на каком-либо шаге пути,
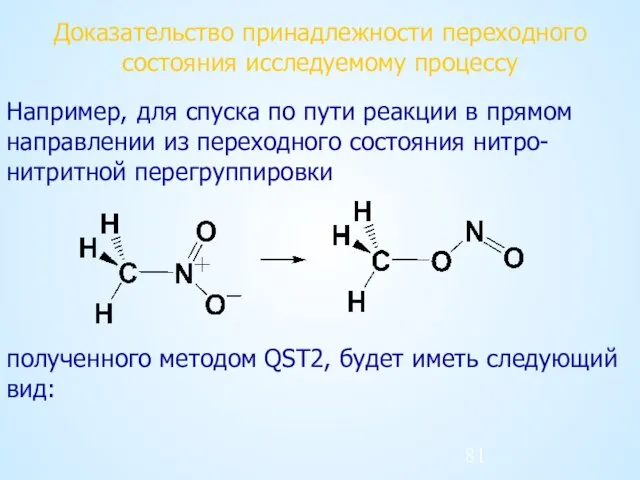
- 81. Доказательство принадлежности переходного состояния исследуемому процессу Например, для спуска по пути реакции в прямом направлении из
- 82. Доказательство принадлежности переходного состояния исследуемому процессу %mem=200Mb %chk=NNR_qst2f.chk #N PM3 irc=(RCFC,MaxCycle=50,StepSize=3,MaxPoints=399, Forward) SCF=(InCore,MaxCycle=500) Trans=Incore Geom=CheckPoint Guess=Read
- 83. Доказательство принадлежности переходного состояния исследуемому процессу В данном примере используются считывание начального приближения (Guess=Read), силовых констант
- 84. Доказательство принадлежности переходного состояния исследуемому процессу В выходном файле Gaussian печатает значения внутренних координат для структур,
- 85. Фрагмент выходного файла спуска в прямом направлении (Forward) из переходного состояния нитро-нитритной перегруппировки (полученного методом прямого
- 86. Фрагмент выходного файла спуска в прямом направлении (Forward) из переходного состояния нитро-нитритной перегруппировки (полученного методом прямого
- 87. Фрагмент выходного файла спуска в прямом направлении (Forward) из переходного состояния нитро-нитритной перегруппировки (полученного методом прямого
- 88. Фрагмент выходного файла спуска в прямом направлении (Forward) из переходного состояния нитро-нитритной перегруппировки (полученного методом прямого
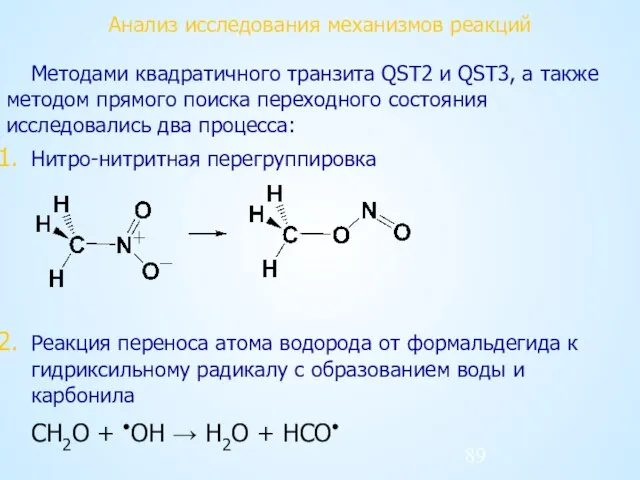
- 89. Анализ исследования механизмов реакций Методами квадратичного транзита QST2 и QST3, а также методом прямого поиска переходного
- 90. Анализ исследования механизмов реакций Если проанализировать результаты спусков по пути реакции из найденных нами переходных состояний
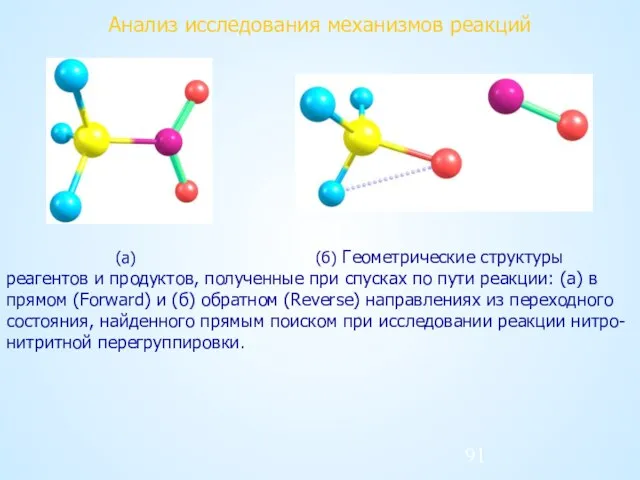
- 91. Анализ исследования механизмов реакций (а) (б) Геометрические структуры реагентов и продуктов, полученные при спусках по пути
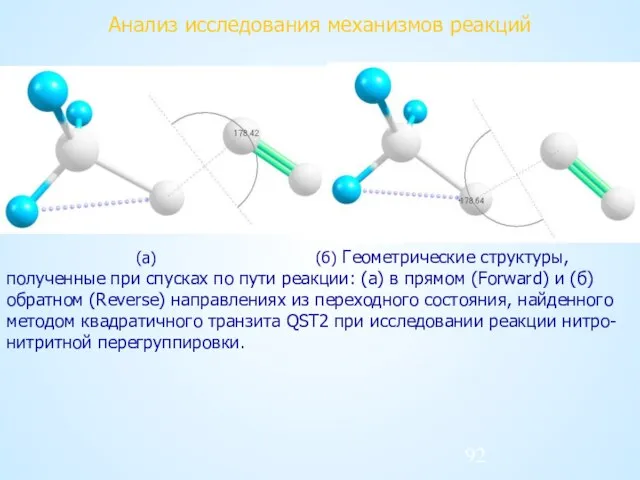
- 92. Анализ исследования механизмов реакций (а) (б) Геометрические структуры, полученные при спусках по пути реакции: (а) в
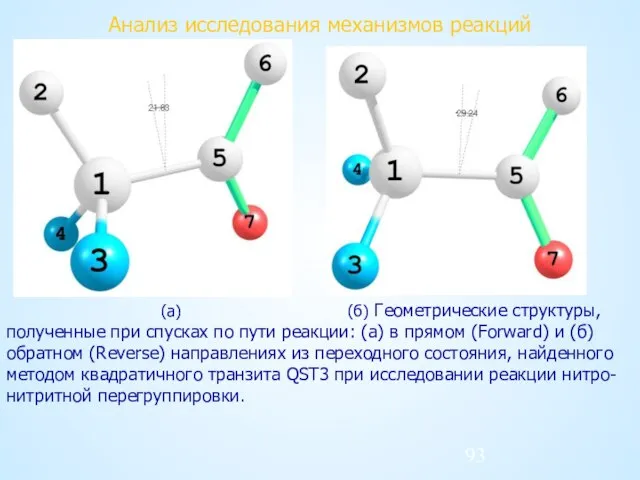
- 93. Анализ исследования механизмов реакций (а) (б) Геометрические структуры, полученные при спусках по пути реакции: (а) в
- 94. Анализ исследования механизмов реакций Если проанализировать результаты спусков по пути реакции из найденных нами переходных состояний
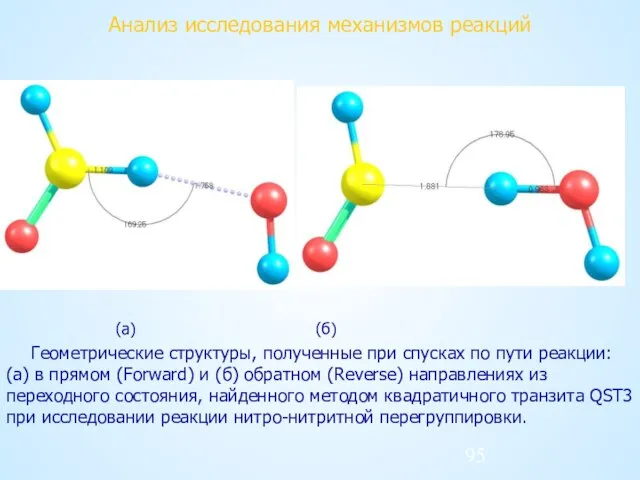
- 95. Анализ исследования механизмов реакций (а) (б) Геометрические структуры, полученные при спусках по пути реакции: (а) в
- 96. Этапы выполнения квантово-химического исследования постановка задачи исследования механизма реакции, куда входит поиск литературы по заданной тематике,
- 97. Расчет энтальпии активации реакции Убедившись, что найденное переходное состояние действительно относится к изучаемой реакции, можно построить
- 98. Расчет энтальпии активации реакции Для более точной оценки энергий активации необходимо добавить к энергии каждой из
- 99. Расчет энтальпии активации реакции где ΔH≠ − энтальпия реакции; ΔH≠f − энтальпия образования переходного состояния, рассчитываемая
- 100. Расчет свободной энергии Гиббса и энтропии активации где ΔG≠ − свободная энергия Гиббса активации; ΔG≠f −
- 101. где k – константа скорости реакции; ΔE ≠ - энергия активации реакции; A – предэкспоненциальный множитель;
- 102. Пример расчета энтальпии, свободной энергии Гиббса и энтропии активации для реакции нитро-нитритной перегруппировки: для прямой реакции:
- 103. Расчет энтальпии образования соединений Расчет энтальпии образования соединений выполняется по формуле где − энтальпия образования исследуемого
- 104. Расчет энергии Гиббса соединений Расчет энергии Гиббса соединений выполняется по формуле где − энергия Гиббса исследуемого
- 105. Расчет энтропии соединений Расчет энтропии соединений выполняется по формуле где − энтропия исследуемого соединения (Дж/моль⋅К); −
- 106. Расчет энальпии реакции Расчет энтальпии реакции соединений выполняется по одной из формул: где − энтальпия реакции;
- 108. Скачать презентацию

















































































 Восприятие (перцепция)
Восприятие (перцепция) Презентация на тему Здоровьесберегающая среда классной комнаты
Презентация на тему Здоровьесберегающая среда классной комнаты Этапы развития жизни на Земле
Этапы развития жизни на Земле Программы повышения результативности персонала
Программы повышения результативности персонала Основные документы
Основные документы Кружок «Юный музеевед»
Кружок «Юный музеевед» Содержание и проблемы реализации государственной программы Доступная среда для инвалидов и людей с ограниченными возможностями
Содержание и проблемы реализации государственной программы Доступная среда для инвалидов и людей с ограниченными возможностями Решения FTTx
Решения FTTx Игуана
Игуана Презентация на тему Лагеря смерти
Презентация на тему Лагеря смерти  Портал (правки)
Портал (правки) Цель Конкурса – выявление и распространение инновационного педагогического опыта в области преподавания физической культуры и ф
Цель Конкурса – выявление и распространение инновационного педагогического опыта в области преподавания физической культуры и ф Пожертвования
Пожертвования Политика качества
Политика качества Односоставные предложения в произведениях Ивана Алексеевича Бунина
Односоставные предложения в произведениях Ивана Алексеевича Бунина Азаматтық іс жүргізудегі үшінші түлғалар
Азаматтық іс жүргізудегі үшінші түлғалар Каток под открытым небом
Каток под открытым небом От повышения качества обучения школьников к повышению доходов педагогов
От повышения качества обучения школьников к повышению доходов педагогов Основные факторы, влияющие на электоральное поведение граждан
Основные факторы, влияющие на электоральное поведение граждан Исследовательский проект«Река Ихаланийоки»
Исследовательский проект«Река Ихаланийоки» Углы, связанные с окружностью
Углы, связанные с окружностью Презентация на тему Фольклор урок
Презентация на тему Фольклор урок  ЦЕНТР МЕЖДУНАРОДНОГООБРАЗОВАНИЯ (ЦМО) СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ЦЕНТР МЕЖДУНАРОДНОГООБРАЗОВАНИЯ (ЦМО) СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ Органы государственной власти
Органы государственной власти Фотография. Искусство фотопейзажа и интерьера. Видео. Правила съёмки пейзажа
Фотография. Искусство фотопейзажа и интерьера. Видео. Правила съёмки пейзажа Презентация на тему Киевское и Черниговское княжества
Презентация на тему Киевское и Черниговское княжества Семинар Мобильные приложения 4.10.22
Семинар Мобильные приложения 4.10.22 Презентация на тему Происхождение и эволюция человека
Презентация на тему Происхождение и эволюция человека