Содержание
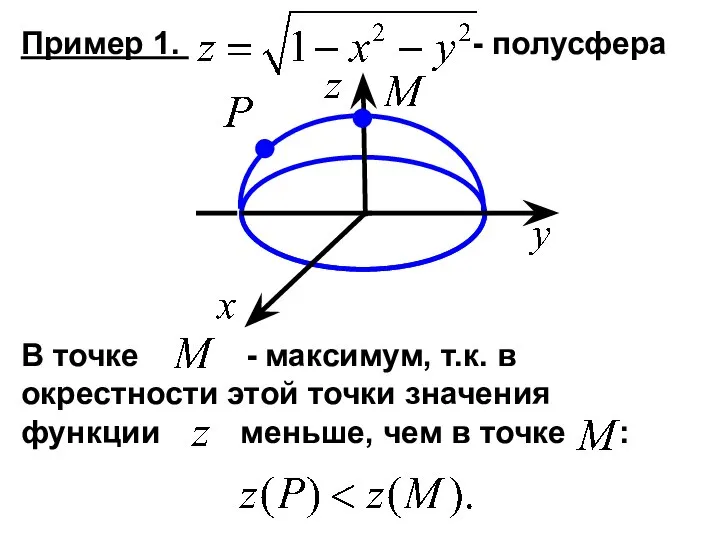
- 2. Пример 1. - полусфера В точке - максимум, т.к. в окрестности этой точки значения функции меньше,
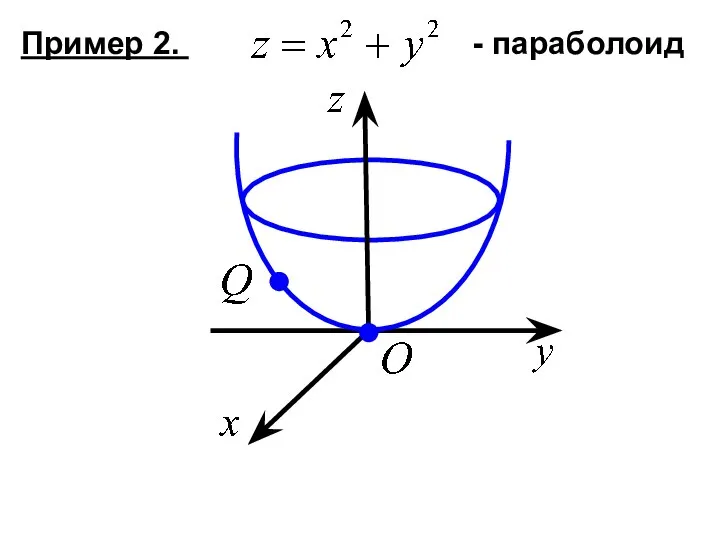
- 3. Пример 2. - параболоид
- 4. В точке - минимум, т.к. в окрестности этой точки значения функции больше, чем в точке :
- 5. Также, как и в случае функции одной переменной для нахождения экстремума находят критические точки. Это точки,
- 6. Следовательно, точки экстремума следует искать среди критических точек. Однако существуют критические точки, не являющиеся точками экстремума.
- 7. Пусть - критическая точка. Находим Составим определитель
- 8. Возможны случаи: Экстремума нет Требуется дополнительное исследование
- 9. Пример. Найти экстремумы функции 1) Находим и
- 10. 2) Составим систему уравнений
- 11. Подставим во второе уравнение или Получили две критические точки и
- 12. 3) Находим
- 13. 4) Рассмотрим и находим значения вторых производных в этой точке: Следовательно экстремума нет.
- 14. 4) Рассмотрим В точке функция имеет экстремум, т.к.
- 15. Чтобы выяснить, max или min в точке смотрим на знак или Ответ: функция имеет в точке
- 16. 1) Найти область определения функций Самостоятельная работа №2 2) Найти частные производные первого и второго порядка
- 18. Условный экстремум: метод множителей Лагранжа
- 24. Пример идея: сведём уравнение ,задающее функцию двух переменных ,к функции одной переменной с помощью уравнения связи
- 27. cужение исходной функции -функцию исследуем на экстремум
- 33. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА
- 37. исключить λ,выразив из первых двух уравнений и приравняв результаты; ВЫРАЗИТЬ из первого уравнения X,из второго –Y
- 38. Составить достаточные условия экстремума
- 54. Скачать презентацию








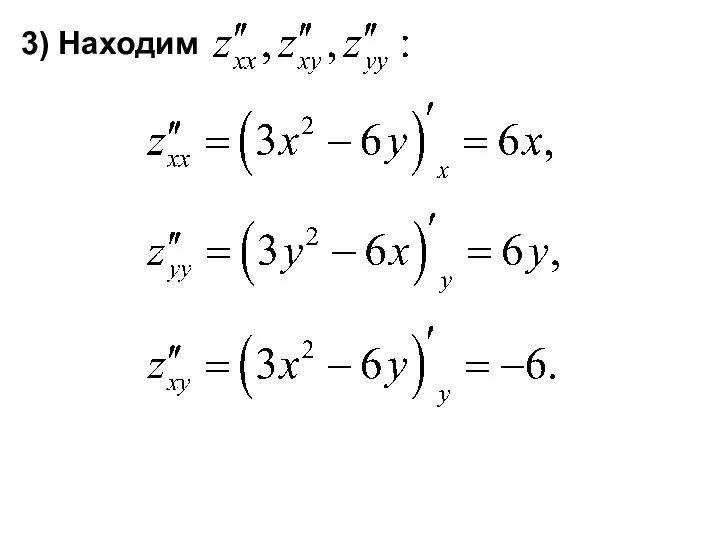








































 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»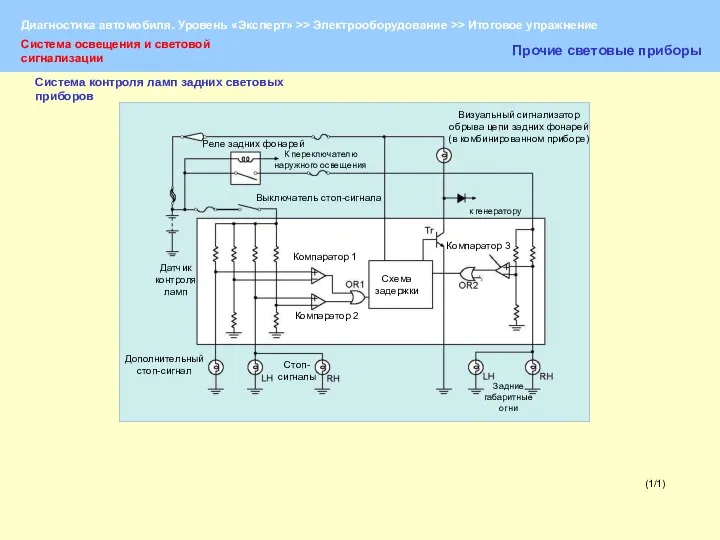 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс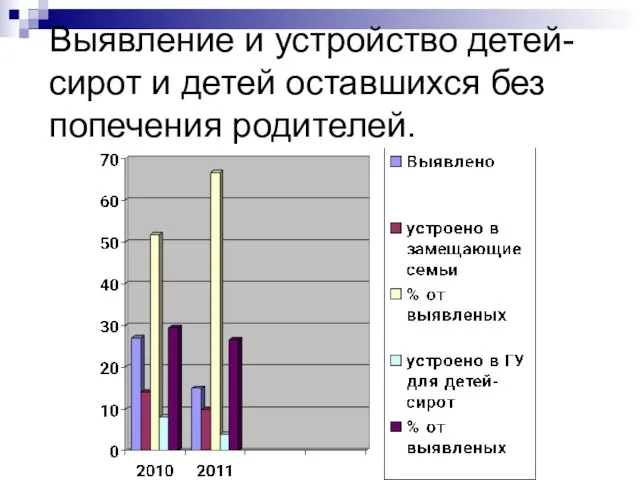 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства