Содержание
Слайд 2Пояснительная записка
Данный курс рассчитан на 17 часов (I полугодие).
Квадратные уравнения
Пояснительная записка
Данный курс рассчитан на 17 часов (I полугодие).
Квадратные уравнения

– это фундамент, на котором строится здание алгебры. Квадратные уравнения часто находят применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств (10-11 классы). Все учащиеся умеют решать квадратные уравнения, начиная со школьной скамьи (8 класса).
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать любые уравнения. На занятиях курса рассматриваются десять способов решения квадратных уравнений.
В материалах курса доступное и мотивированное изложение теоретических сведений. Развитие содержания идёт по спирали, позволяющей неоднократно возвращаться на новом уровне ко всем вопросам.
Программа курса по выбору приобщает учеников к постоянно меняющемуся, развивающемуся знанию, к новой информации; помогает удовлетворять познавательную потребность учащихся; выстраивает такую учебную траекторию, двигаясь по которой ученики достигают максимально возможного уровня развития интеллекта, а также предусматривает изучение проблемы, которая интегрирует знания со структурами мышления: развитие продуктивного мышления и навыком его практического применения.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать любые уравнения. На занятиях курса рассматриваются десять способов решения квадратных уравнений.
В материалах курса доступное и мотивированное изложение теоретических сведений. Развитие содержания идёт по спирали, позволяющей неоднократно возвращаться на новом уровне ко всем вопросам.
Программа курса по выбору приобщает учеников к постоянно меняющемуся, развивающемуся знанию, к новой информации; помогает удовлетворять познавательную потребность учащихся; выстраивает такую учебную траекторию, двигаясь по которой ученики достигают максимально возможного уровня развития интеллекта, а также предусматривает изучение проблемы, которая интегрирует знания со структурами мышления: развитие продуктивного мышления и навыком его практического применения.
Слайд 710. СПОСОБ: Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была
10. СПОСОБ: Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была

более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39».
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39».
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
D
X
C
A
X
B
Следующая -
«Хранители»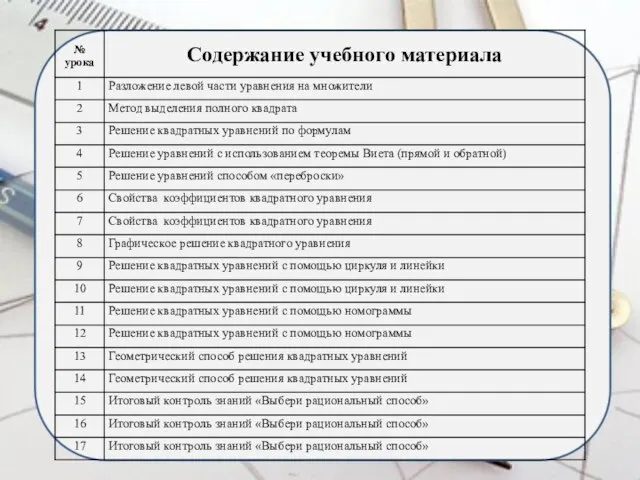



 Измельчительно-режущее оборудование
Измельчительно-режущее оборудование Комиссия по профориентационной работе
Комиссия по профориентационной работе Альберт Эйнштейн – личность века
Альберт Эйнштейн – личность века Тестовая игра Кокология
Тестовая игра Кокология Сбор нагрузок на 1м2 плиты перекрытия жилого здания
Сбор нагрузок на 1м2 плиты перекрытия жилого здания Урок литературного чтения И. А. Крылов Басня «Ворона и Лисица»
Урок литературного чтения И. А. Крылов Басня «Ворона и Лисица» Интерактивный учебник
Интерактивный учебник Modal verb must
Modal verb must Обзор продуктов Konica Minolta
Обзор продуктов Konica Minolta Обратный поток
Обратный поток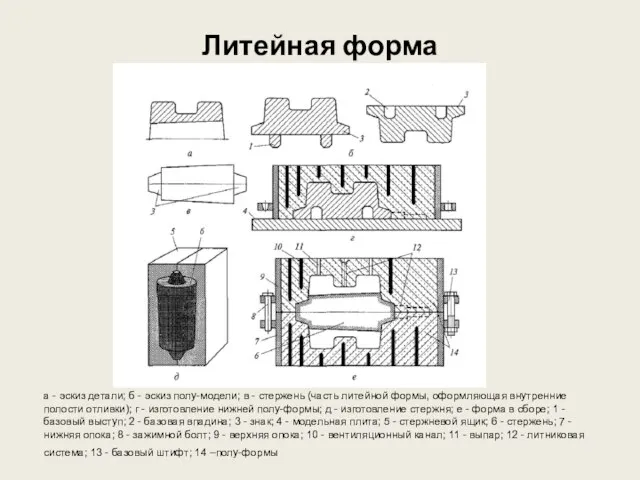 Литейная форма
Литейная форма Подбор сотрудника
Подбор сотрудника Технические средства телекоммуникационных технологий
Технические средства телекоммуникационных технологий Проектирование сварных и комбинированных заготовок
Проектирование сварных и комбинированных заготовок Конфликтологическая парадигма. Идеи Ч.Р.Миллса, Р.Дарендорфа, Л.Козера
Конфликтологическая парадигма. Идеи Ч.Р.Миллса, Р.Дарендорфа, Л.Козера Акварель Составлено доцентом кафедры изобразительного искусства СыктГУ Торлоповой Натальей Геннадьевной 2006
Акварель Составлено доцентом кафедры изобразительного искусства СыктГУ Торлоповой Натальей Геннадьевной 2006 Русская юзабилити в изгнании
Русская юзабилити в изгнании АРТЕРИАЛЬНАЯ ГИПОТОНИЯ
АРТЕРИАЛЬНАЯ ГИПОТОНИЯ Земельный участокв Ставропольском районе Самарской области
Земельный участокв Ставропольском районе Самарской области ?
? Городской конкурс Читатель года
Городской конкурс Читатель года У.У. Сойер
У.У. Сойер Презентация на тему Деревья леса
Презентация на тему Деревья леса История возникновения шахмат
История возникновения шахмат Инфракрасное и ультрафиолетовое излучения
Инфракрасное и ультрафиолетовое излучения ПРИМЕНЕНИЕ ПРОЕКТНОЙ ТЕХНОЛОГИИ В РАБОТЕ С ОДАРЕННЫМИ ДЕТЬМИ
ПРИМЕНЕНИЕ ПРОЕКТНОЙ ТЕХНОЛОГИИ В РАБОТЕ С ОДАРЕННЫМИ ДЕТЬМИ Гусеничный пандус
Гусеничный пандус Сила достижения
Сила достижения