Содержание
- 2. 1. Электромагнитное поле. Электрические заряды. Закон сохранения заряда. Электромагнитное поле является одной из форм материи и
- 3. Электрический заряд - неотъемлемое свойство заряженных элементарных частиц. Заряженная частица не может «потерять» заряд так же,
- 4. 2. Закон Кулона Количественно взаимодействие неподвижных точечных зарядов определяется законом Кулона Согласно закону Кулона, электрическая сила,
- 5. 3. Напряженность электрического поля Каждый заряд создает в окружающем пространстве электрическое поле (ЭП) и через него
- 6. Модуль вектора напряженности поля точечного заряда равен Единицы измерения напряженности [В/м или Н/Кл] Принцип суперпозиции: результирующая
- 8. 4. Потенциал электростатического поля Пусть точечный положительный заряд q перемещается на расстояние dl в электрическом поле.
- 9. Отношение потенциальной энергии к пробному заряду называют потенциалом: Потенциал – это энергетическая характеристика электрического поля. Учитывая,
- 10. Эквипотенциальная поверхность – это поверхность, все точки которой имеют одинаковый потенциал. Эквипотенциальные поверхности имеют следующие свойства:
- 11. 5. Связь между напряженностью и потенциалом электростатического поля При перемещении заряда q из точки 1 в
- 12. или Напряженность в каждой точке электростатического поля равна по абсолютной величине и противоположна по направлению градиенту
- 13. 6. Поток вектора напряженности Единица потока вектора напряженности электростатического поля В∙м.
- 14. 7. Теорема Остроградского-Гаусса Определим поток вектора напряженности через замкнутую сферическую поверхность, в центре которой находится положительный
- 15. Теорема Остроградского-Гаусса: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме
- 16. 8. Применение теоремы Остроградского-Гаусса Если заряд Q протяженный, его разбивают на элементарные порции dQ, которые можно
- 17. 8.1 Напряженность электрического поля равномерно заряженной сферы Пусть общий заряд сферы радиуса R равен Q. Поскольку
- 18. 8.2 Напряженность поля объемно заряженного шара Пусть шар радиуса R с общим зарядом Q заряжен равномерно
- 19. 8.3 Напряженность поля равномерно заряженной бесконечной плоскости Поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю,
- 20. 8.4 Напряженность поля двух параллельных, бесконечных, разноименно заряженных плоскостей На рисунке верхние стрелки соответствуют полю от
- 21. 8.5 Напряженность поля вблизи равномерно заряженной нити (равномерно заряженного бесконечного цилиндра) Пусть нить длиной L несет
- 22. Проводники и диэлектрики в электрическом поле
- 23. В зависимости от способности проводить электрический ток все вещества делятся на проводники, диэлектрики (изоляторы) и полупроводники.
- 24. 1. Диполь. Поляризация диполя Электрический диполь – система двух равных по модулю разноименных точечных зарядов (+Q,
- 25. У некоторых диэлектриков (Н2О, NH3, SO2, СО и др.) молекулы имеют асимметричное строение: центры «тяжести» отрицательных
- 26. Другие диэлектрики (N2, Н2, О2, СО2, СН4 и др.) имеют симметричное строение молекул. У них центры
- 27. Поляризация диэлектриков ослабляет в ε раз электрическое поле в них. Относительная диэлектрическая проницаемость ε есть величина
- 28. 2. Проводники в электрическом поле Под влиянием электрического поля свободные электроны проводника начнут перемешаться против поля.
- 29. При сообщении уединенному проводнику заряда q его потенциал изменяется на Δφ. Опыт показывает, что между q
- 30. 3. Конденсаторы Приборы, способные накапливать заряд, называют конденсаторами. Чтобы электроемкость С проводников не зависела от окружающих
- 31. Электроемкостью конденсатора называется физическая величина численно равная отношению заряда конденсатора к абсолютной величине разности потенциалов между
- 32. 4. Соединение конденсаторов - при параллельном соединении конденсаторов емкость равна сумме емкостей конденсаторов или
- 33. При последовательном соединении заряды, всех обкладок будут одинаковыми по величине и равными Q, а разность потенциалов
- 35. Скачать презентацию
































 Вытяжка. Основные группы получаемых деталей
Вытяжка. Основные группы получаемых деталей Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ
Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ Эволюция денег
Эволюция денег Higher education in the USA
Higher education in the USA Разработка игр в HTML5. Опыт портирования Doodle God. Николай Котляров, JoyBits Ltd.
Разработка игр в HTML5. Опыт портирования Doodle God. Николай Котляров, JoyBits Ltd. КККК.tif
КККК.tif В мире прекрасного
В мире прекрасного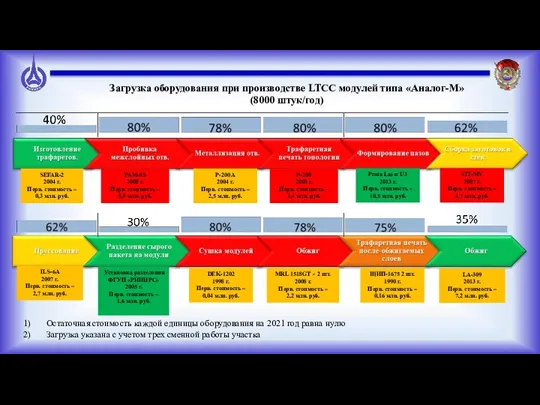 Загрузка оборудования при производстве LTCC модулей типа Аналог-М
Загрузка оборудования при производстве LTCC модулей типа Аналог-М Состав и виды бюджетных расходов на образование
Состав и виды бюджетных расходов на образование Памятники архитектуры в России
Памятники архитектуры в России Общественное движение: либералы и консерваторы
Общественное движение: либералы и консерваторы Новогодние персонажи со всего света. Дед Мороз
Новогодние персонажи со всего света. Дед Мороз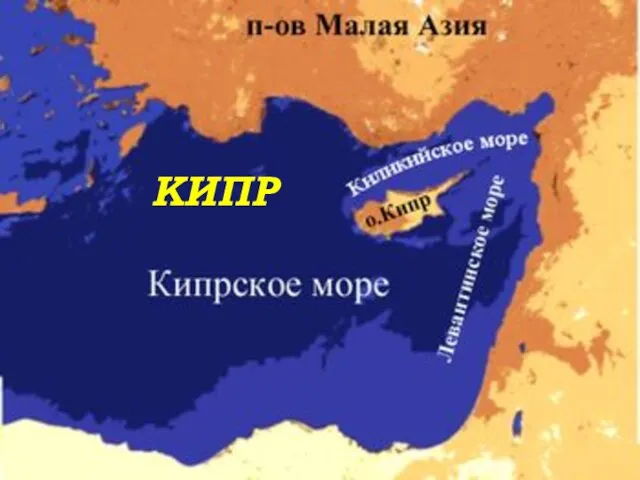 Кипр
Кипр Общественно-политическое развитие России в 1894 – 1904 гг
Общественно-политическое развитие России в 1894 – 1904 гг NEWS Интервью Агнеты шведскому журналу M- Magasin- Вы когда-нибудь слушаете песни АББА? - Прошло много времени, прежде чем я начала слушать
NEWS Интервью Агнеты шведскому журналу M- Magasin- Вы когда-нибудь слушаете песни АББА? - Прошло много времени, прежде чем я начала слушать Проект Званый обед
Проект Званый обед Тема 3. Несостоятельность (банкротство)
Тема 3. Несостоятельность (банкротство) British monarch Queen Elizabeth II
British monarch Queen Elizabeth II Учёт и анализ оплаты труда и расчётов с рабочими и служащими (на материалах УП Завод Радиан, г. Минск)
Учёт и анализ оплаты труда и расчётов с рабочими и служащими (на материалах УП Завод Радиан, г. Минск) Вот это место
Вот это место Опорно-двигательная система. Состав и строение костей
Опорно-двигательная система. Состав и строение костей Экономико - географическая характеристика Бразилии
Экономико - географическая характеристика Бразилии Команды Фортуна
Команды Фортуна АМЕРИКАНСКИЙ И БРИТАНСКИЙ АНГЛИЙСКИЙ.
АМЕРИКАНСКИЙ И БРИТАНСКИЙ АНГЛИЙСКИЙ. Профессиональное портфолио преподавателя татарского языка и литературы
Профессиональное портфолио преподавателя татарского языка и литературы Пройти по тихим школьным этажам
Пройти по тихим школьным этажам Вальс. Основные элементы вальса
Вальс. Основные элементы вальса