Электронное сопровождение к изучению темы: «Теорема Пифагора»

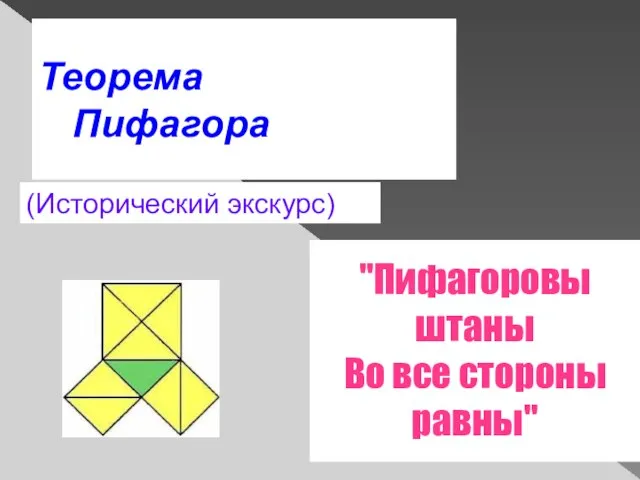
Теорема
Пифагора
(Исторический экскурс)
"Пифагоровы штаны
Во все стороны равны"

«Геометрия владеет
двумя сокровищами:
одно из них –
это теорема Пифагора»
Задачи:
Иоганн Кеплер

ТеоремаПифагора!
Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо о ней знает подавляющее большинство населения планеты, хотя доказать ее способна лишь очень незначительная его часть.

В чем же причина такой популярности
«пифагоровых штанов»?
Знатоки утверждают, что причин здесь три:
б) красота,
а) простота,
в) значимость.

Формулировки теоремы Пифагора различны. Общепринятой считается следующая:
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетовкатетов».
Во времена Пифагора формулировка теоремы звучала так:
«Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах».

Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось:
“Dons asinorum” -
«ослиный мост»
или
“elefuga” -
«бегство убогих»
а сама теорема –
«ветряной мельницей»,
«теоремой – бабочкой»
илиили
«теоремой невесты»
Сейчас известно около 150 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.)

Различные способы
доказательства теоремы
Доказательства, основанные на использовании понятия равновеликости фигур
Аддитивные доказательства (основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе
Доказательства методом достроения
Алгебраический метод доказательства
И т.д.

Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий
Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол.

Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике.
Как свидетельствуют летописи, в Древнем Китае уже около 2200 года до н.э. для треугольника со сторонами 3, 4, 5 было найдено правило «гоу-гу», с помощью которого можно было по известным гипотенузе и одному из катетов находить другой неизвестный катет, а также гипотенузу, если известны оба катета.

В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила веревки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). Алтари по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.

В Древнем Вавилоне это свойство не только треугольника со сторонами 3, 4, 5, но и вообще всех прямоугольных треугольников было хорошо известно. Так, в одном из самых ранних вавилонских математических текстов содержится следующая изящная задача:
«Палка длиной 1/2, прислонена к стене. Ее верхний конец опустили на 1/10. Как далеко отодвинется ее нижний конец?»

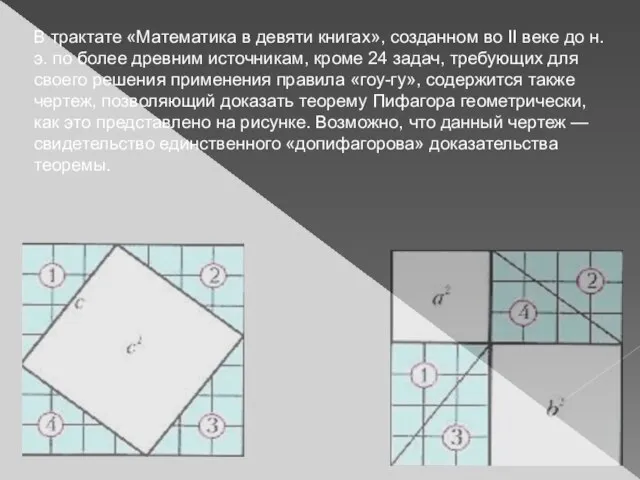
В задаче, как видим, по данным гипотенузе c = 1/2 и одному из катетов b = 1/2 - 1/10 = 2/5 необходимо найти второй катет. Его, как и положено, вавилонянин определяет «по Пифагору»:

В трактате «Математика в девяти книгах», созданном во II веке до н.э. по более древним источникам, кроме 24 задач, требующих для своего решения применения правила «гоу-гу», содержится также чертеж, позволяющий доказать теорему Пифагора геометрически, как это представлено на рисунке. Возможно, что данный чертеж — свидетельство единственного «допифагорова» доказательства теоремы.

Большая часть доказательств теоремы Пифагора выполнена геометрическими методами, среди которых значительное место занимает метод разложения. Сущность метода разложения заключается в том, что квадрат, построенный на гипотенузе, с одной стороны, и квадраты, построенные на катетах, с другой, складываются из равных частей. Простейший пример применения этого метода имеем при доказательстве теоремы Пифагора для равнобедренного прямоугольного треугольника (см. рис.). Из этого рисунка все так понятно, что комментировать его не требуется. Как писал в подобных случаях индийский математик XII века Бхаскара: «Смотри!»

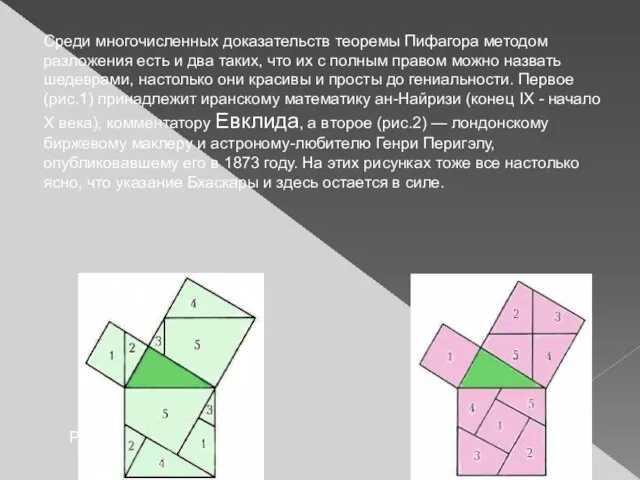
Среди многочисленных доказательств теоремы Пифагора методом разложения есть и два таких, что их с полным правом можно назвать шедеврами, настолько они красивы и просты до гениальности. Первое (рис.1) принадлежит иранскому математику ан-Найризи (конец IX - начало Х века), комментатору Евклида, а второе (рис.2) — лондонскому биржевому маклеру и астроному-любителю Генри Перигэлу, опубликовавшему его в 1873 году. На этих рисунках тоже все настолько ясно, что указание Бхаскары и здесь остается в силе.

Таким образом, теорема Пифагора в виде простейших угломерных приспособлений, частных и общих математических задач и чертежей обнаружена в памятниках культуры древних египтян, вавилонян, китайцев и индийцев задолго до Пифагора. Но среди этих памятников нет ни одного, за исключением китайского математического трактата, в котором имелись бы хотя бы указания на доказательство теоремы.

Как утверждают все античные авторы, Пифагор первый дал полноценное доказательство теоремы, носящей его имя. К сожалению, мы не знаем, в чем оно состояло, потому что древние математики и писатели об этом умалчивают, а от самого Пифагора и ранних пифагорейцев до нас не дошло ни одного письменного документа.

Теорема Пифагора – одна из самых главных теорем геометрии. Из нее или с ее помощью можно вывести большинство теорем. Сама же теорема Пифагора замечательна тем, что она проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное практическое значение: она применяется в геометрии буквально на каждом шагу.

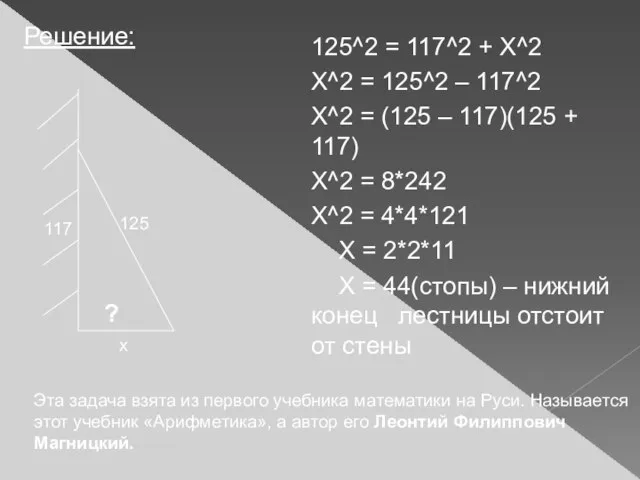
Старинные задачи:
Случися некоему человеку к стене лествицу прибрати, у стены же тоя высота есть 117 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.

Решение:
125^2 = 117^2 + Х^2
X^2 = 125^2 – 117^2
X^2 = (125 – 117)(125 + 117)
X^2 = 8*242
X^2 = 4*4*121
X = 2*2*11
X = 44(стопы) – нижний конец лестницы отстоит от стены
Эта задача взята из первого учебника математики на Руси. Называется этот учебник «Арифметика», а автор его Леонтий Филиппович Магницкий.

Часто математики записывали свои задачи в стихотворной форме. Вот одна из задач индийского математика XII века Бхаскары:
2. На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?

Решение:
3^2 + 4^2 = x^2
X^2 = 25
X = 5(футов) – длина отломленной части ствола;
3 + 5 = 8(футов) – высота тополя.

Еще одна задача древних индусов также предложенная в стихах:
3.Над озером тихим,
С полфута размером высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?

(Х + ½)^2 – X^2 = 2^2
X^2 + X + ¼ - X^2 = 4
X = 3 ¾ (футов) –
глубина озера
Решение:

Сейчас теорему Пифагора знают практически все, кто когда-либо изучал планиметрию.
Считается, что если мы хотим дать знать внеземным цивилизациям о существовании разумной жизни на Земле, то следует посылать в космос изображение Пифагоровой фигуры. Так как если эту информацию смогут принять мыслящие существа, то они без сложной дешифровки сигнала поймут, что на земле существует достаточно развитая цивилизация.

Источники информации:
www.1september.ru/ru
http://root/
//images.yandex.ru/yandsearch?
И. Глейзер. История математики в школе.
А.Д.Александров и др. Геометрия 7-9
Атанасян и др. Геометрия 7-9
В.Н.Руденко, Г.А.Бахурин Геометрия 7-9
В.Д.Чистяков. Старинные задачи по элементарной математике

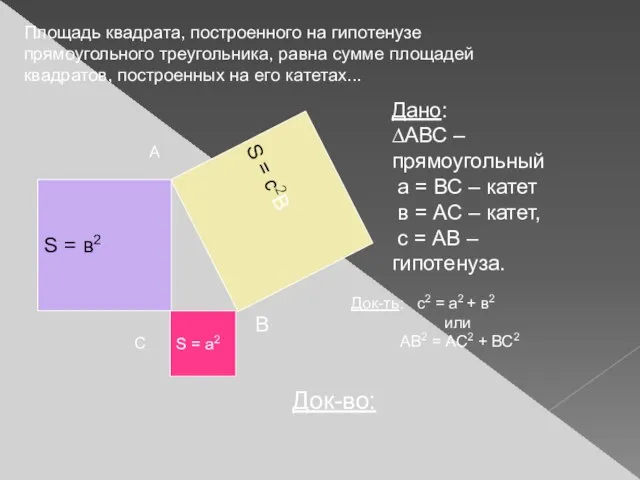
Теорема.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Дано: прямоугольный
треугольник с катетами a, b и гипотенузой c.
Док-ть: a^2 + b^2 = c^2

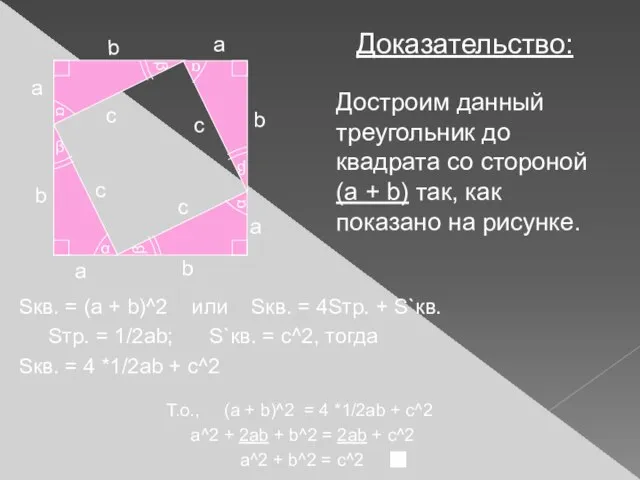
Доказательство:
Достроим данный треугольник до квадрата со стороной (a + b) так, как показано на рисунке.
Sкв. = (a + b)^2 или Sкв. = 4Sтр. + S`кв.
Sтр. = 1/2ab; S`кв. = c^2, тогда
Sкв. = 4 *1/2ab + c^2
Т.о., (a + b)^2 = 4 *1/2ab + c^2
a^2 + 2ab + b^2 = 2ab + c^2
a^2 + b^2 = c^2

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах...
S = c2B
S = a2
S = в2
Дано:
∆АВС – прямоугольный
а = ВС – катет
в = АС – катет,
с = АВ – гипотенуза.
A
B
C
Док-ть: с2 = а2 + в2
или
АВ2 = АС2 + ВС2
Док-во:

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко недостоверны. С его именем связано много легенд.
Пифагор – древнегреческийПифагор – древнегреческий ученый (VIVI в. до н.э.)

Достоверно известно, что Пифагор много путешествовал по странам Востока, посещал Египет, Индию и Вавилон, изучал древнюю культуру и достижения науки разных стран.
Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии, куда принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя.

Так на юге Италии, которая была в то время греческой колонией, возникла знаменитая «Пифагорейская школа», сыгравшая важную роль в научной и политической жизни древней Греции.
Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. Однако, в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору.

Именно Пифагору приписывают и доказательство знаменитой геометрической теоремы.
На основе преданий, распространенных известными математиками (Прокл, Плутарх и др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора.
Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили тайной имя своего учителя, так что установить правду о Пифагоре невозможно.

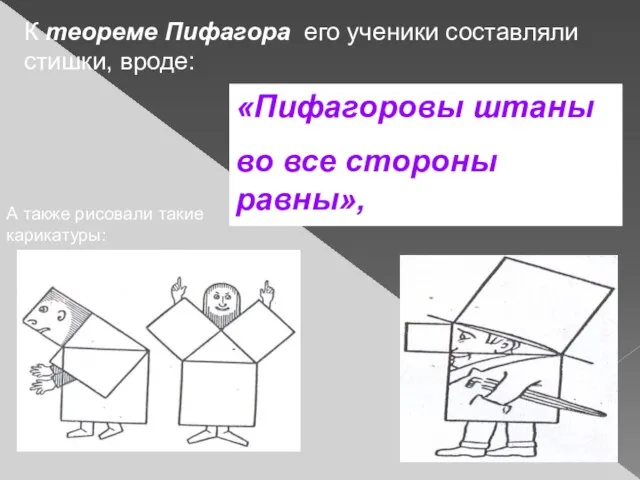
К теореме Пифагора его ученики составляли стишки, вроде:
«Пифагоровы штаны
во все стороны равны»,
А также рисовали такие карикатуры:

Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.
"elefuga"
"Dons asinorum"
Или «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

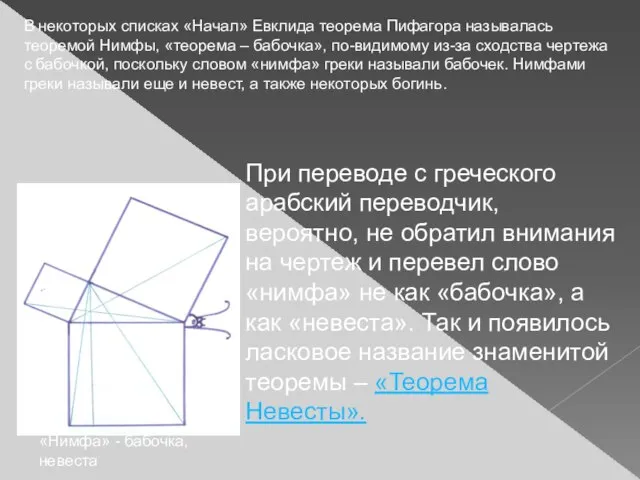
В некоторых списках «Начал» Евклида теорема Пифагора называлась теоремой Нимфы, «теорема – бабочка», по-видимому из-за сходства чертежа с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.
При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса». Самостоятельное «открытие» доказательства теоремы Пифагора будет полезно и современным школьникам.