Электропроводность металлов

Лекция 7/3 Электропроводность металлов
Классическая теория электропроводности металлов
2. Квантовая теория электропроводности металлов
3. Сверхпроводимость

Классическая теория электропроводности металлов
Металлы – хорошие проводники электрического тока.
Носителями электрического тока в металлах являются свободные электроны.
Друде и Лоренцом была создана классическая электронная теория электропроводности металлов.

В ней металлы представляли собой твердые вещества, в узлах которых находятся положительные ионы, совершающие непрерывные колебания у положения равновесия.
Отрицательные электроны представляют собой практически свободные частицы – отрицательно заряженный электронный газ (в качестве модели использовалась модель идеального газа).

В отсутствие электрического поля электроны участвуют лишь в хаотическом движении с
сталкиваясь только с узлами кристаллической решетки.
В электрическом поле электроны приобретают направленное движение против поля и двигаются с ускорением:

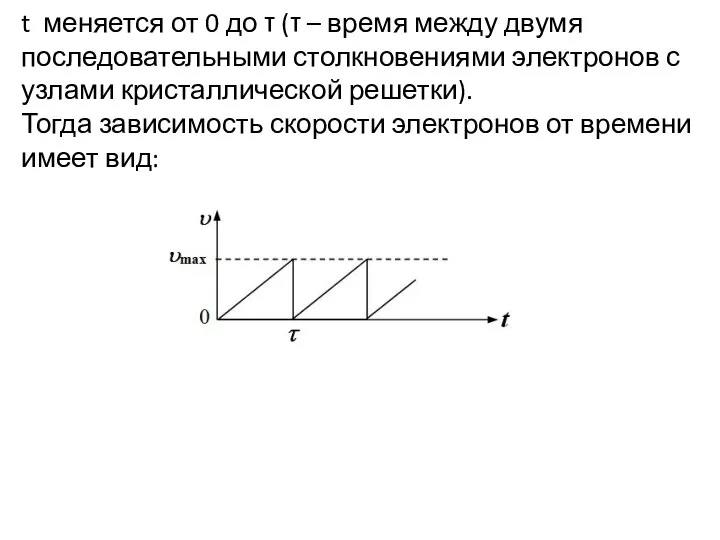
t меняется от 0 до τ (τ – время между двумя последовательными столкновениями электронов с узлами кристаллической решетки).
Тогда зависимость скорости электронов от времени имеет вид:

Учитывая , получим выражения для
удельной проводимости металлического проводника
,
и его сопротивления

Разные металлы имеют:
различные концентрации носителей заряда ne.
разное строение кристаллической решетки и
.
разную скорость теплового движения электронов <υ>.
Следовательно классическая теория электропроводности металлов объясняет:
1) разное сопротивление различных металлов.
2) зависимость сопротивления от температуры

Проблемы классической теории:
1) Использование модели идеального электронного газа приводит к результату, что молярная теплоемкость металлов должна была быть равна 4,5Rгаз (Rгаз=8,31), что противоречило эксперименту.
2) Опыт показывает, что сопротивление R~T, а не

2. Квантовая теория электропроводности металлов
На электроны проводимости в металле действуют сложные, неподдающиеся точному описанию силы:
силы притяжения к атомам металла;
силы взаимодействия электронов между собой;
cилы, связанные с дефектами кристаллического строения металлов.

2. Квантовая теория электропроводности металлов
Для описания движения электрона во внешнем электрическом поле E вводят понятие эффективной массы электрона m* (m*≠me), тогда:
F=m*a => -eE=m*a.
Эффективная масса не определяет ни инертные, ни гравитационные свойства электрона. Она лишь характеризует его взаимодействие с электрическим полем кристалла.

Закон Ома j=σE.
Проводимость металла:
где
ε – модуль упругости кристаллической решетки;
k=1,38.10-23 Дж/К – постоянная Больцмана;
υ – скорость поступательного движения электронов.

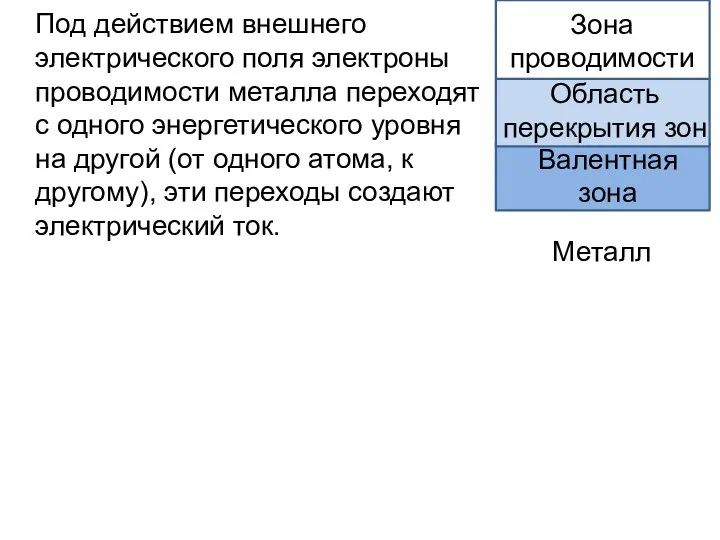
Под действием внешнего электрического поля электроны проводимости металла переходят с одного энергетического уровня на другой (от одного атома, к другому), эти переходы создают электрический ток.
Зона проводимости
Область перекрытия зон
Валентная
зона
Металл

Квантовая физика считает, что электроны при своем движении рассеиваются не на узлах кристаллической решетки, а на фононах, концентрация которых сильно зависит от температуры.

3. Сверхпроводимость
Переход ртути Hg в сверх-проводящее состояние
Состояние с нулевым сопротив-лением R
R<10-5 Ом
Температура (К)
R (Ом)
Камерлинг Оннес 1911 год.

Есть два рода частиц: фермионы и бозоны.
Фермионы – частицы с полуцелым значением спина (s=1/2, 3/2…). Они подчиняются принципу запрета Паули.
Подчиняются статистике Ферми-Дирака.
Пример: электрон, протон, нейтрон и частицы, составленные из нечетного числа фермионов и др.

Бозоны – частицы с целым значением спина (s=1, 2…). Они НЕ подчиняются принципу запрета Паули.
Подчиняются статистике Бозе-Эйнштейна.
Пример: фотон, частицы, составленные из четного числа фермионов и др.

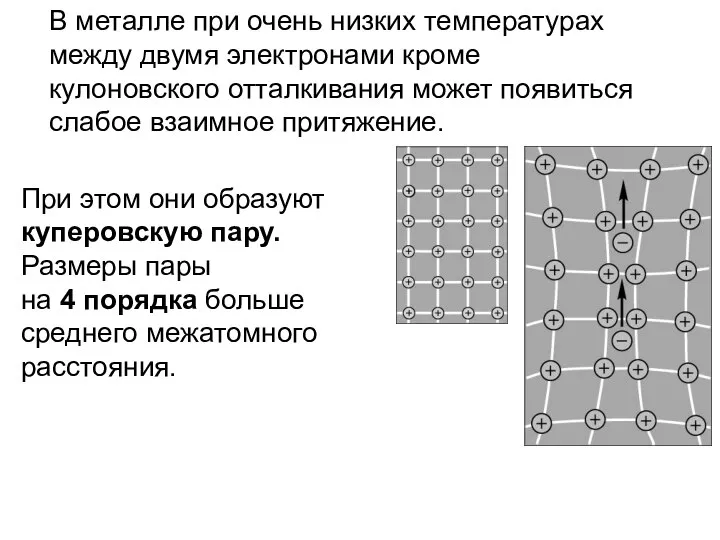
В металле при очень низких температурах между двумя электронами кроме кулоновского отталкивания может появиться слабое взаимное притяжение.
При этом они образуют куперовскую пару. Размеры пары
на 4 порядка больше среднего межатомного расстояния.

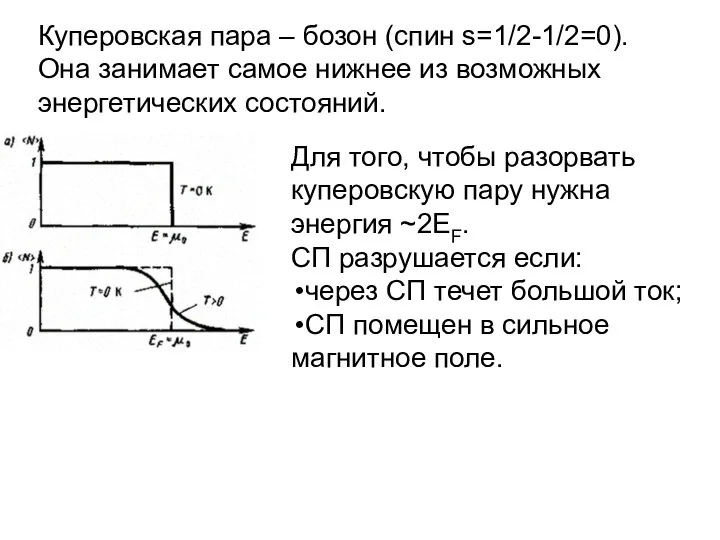
Куперовская пара – бозон (спин s=1/2-1/2=0). Она занимает самое нижнее из возможных энергетических состояний.
Для того, чтобы разорвать куперовскую пару нужна энергия ~2EF.
СП разрушается если:
через СП течет большой ток;
СП помещен в сильное магнитное поле.

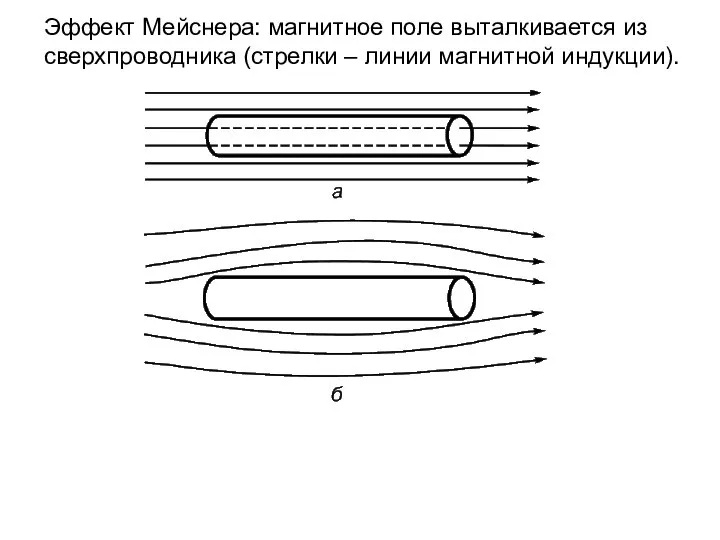
Эффект Мейснера: магнитное поле выталкивается из сверхпроводника (стрелки – линии магнитной индукции).

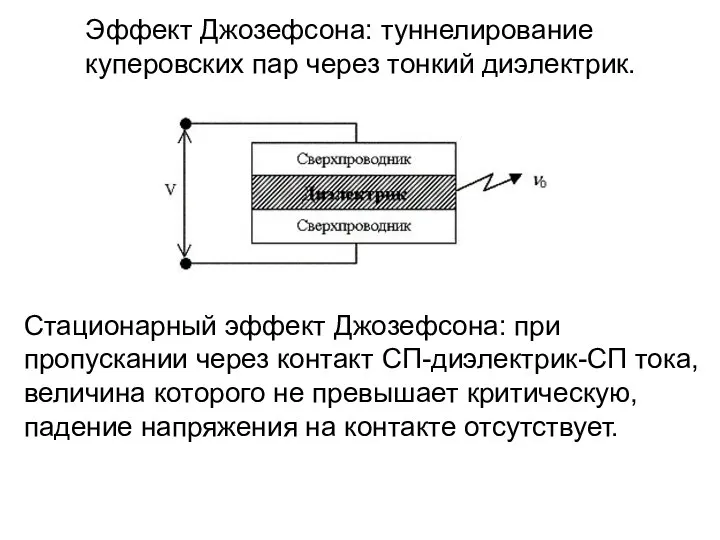
Эффект Джозефсона: туннелирование куперовских пар через тонкий диэлектрик.
Стационарный эффект Джозефсона: при пропускании через контакт СП-диэлектрик-СП тока, величина которого не превышает критическую, падение напряжения на контакте отсутствует.