Электротехника и электроника. Линейные электрические цепи при несинусоидальных периодических токах

ЛИНЕЙНЫЕ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПРИ НЕСИНУСОИДАЛЬНЫХ ПЕРИОДИЧЕСКИХ ТОКАХ
Тема 8

Несинусоидальные токи
Периодическими несинусоидальными токами и напряжениями называются токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону

Разложение периодических функций.
Характеристики несинусоидальных величин
Для анализа процессов в линейных электрических цепях при воздействии на них несинусоидальных токов или напряжений последние обычно разлагаются в ряд Фурье.

Ряд Фурье в тригонометрической форме
Ряд Фурье в тригонометрической форме

Ряд Фурье в тригонометрической форме
Коэффициенты an и bn вычисляются по формулам
– постоянная составляющая, равная среднему
значению функции f(t) за период:

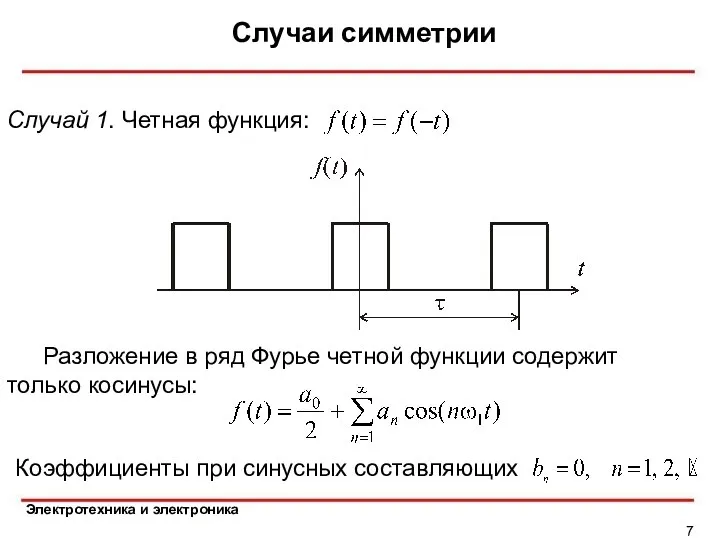
Случаи симметрии
Случай 1. Четная функция:
Разложение в ряд Фурье четной функции содержит
только косинусы:
Коэффициенты при синусных составляющих

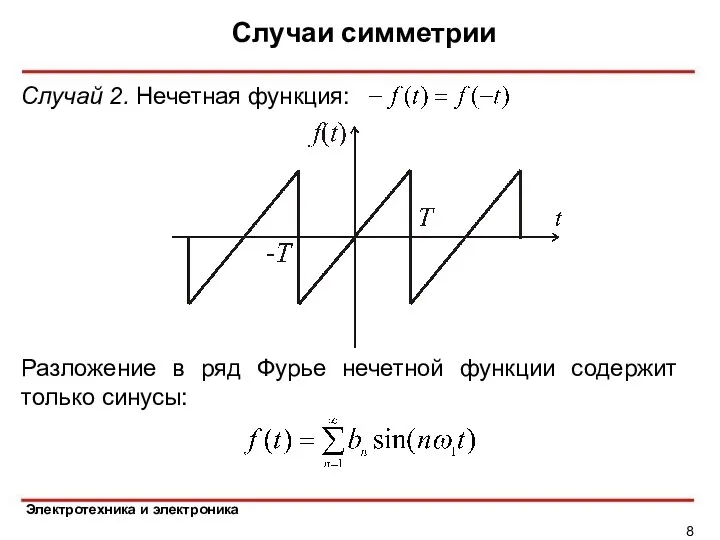
Случаи симметрии
Случай 2. Нечетная функция:
Разложение в ряд Фурье нечетной функции содержит только синусы:

Случаи симметрии
Случай 3. Функция f(t) симметрична относительно оси абсцисс при совмещении двух полупериодов во времени, т. е.
Четные гармоники, а также составляющая равны нулю, т. е.

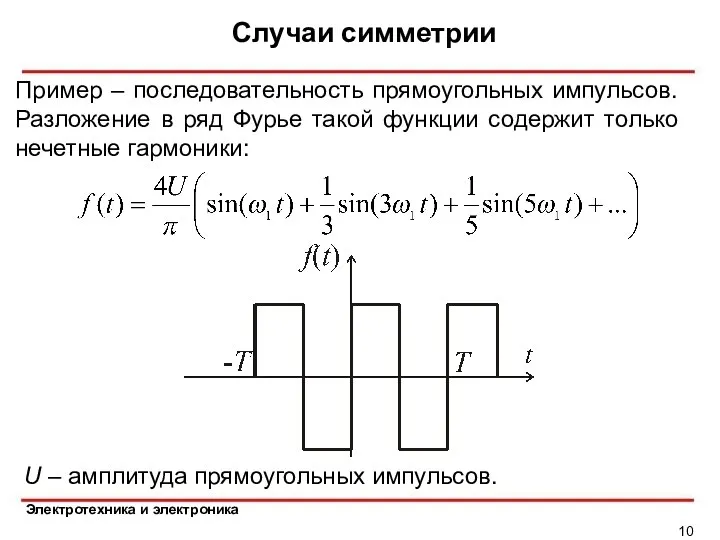
Случаи симметрии
Пример – последовательность прямоугольных импульсов. Разложение в ряд Фурье такой функции содержит только нечетные гармоники:
U – амплитуда прямоугольных импульсов.

Комплексная форма ряда Фурье
Ряд Фурье в тригонометрической форме
Воспользуемся равенствами:

Комплексная форма ряда Фурье
Ряд Фурье примет вид:
Коэффициент an – четная, а bn – нечетная функция индекса n:
Поэтому элемент -jbn можно рассматривать как слагаемое с отрицательным индексом.
,

Комплексная форма ряда Фурье
Изменив нижний предел суммирования на , получим
– комплексный коэффициент ряда Фурье.
В показательной форме:
,

Комплексный частотный спектр
Амплитуды гармоник образуют амплитудный спектр.
Совокупность комплексных коэффициентов гармоник называют комплексным частотным спектром функции
Начальные фазы образуют фазовый спектр.

Комплексный частотный спектр
Используя равенства
Комплексная амплитуда n-й гармоники
получим, что комплексный коэффициент ряда Фурье

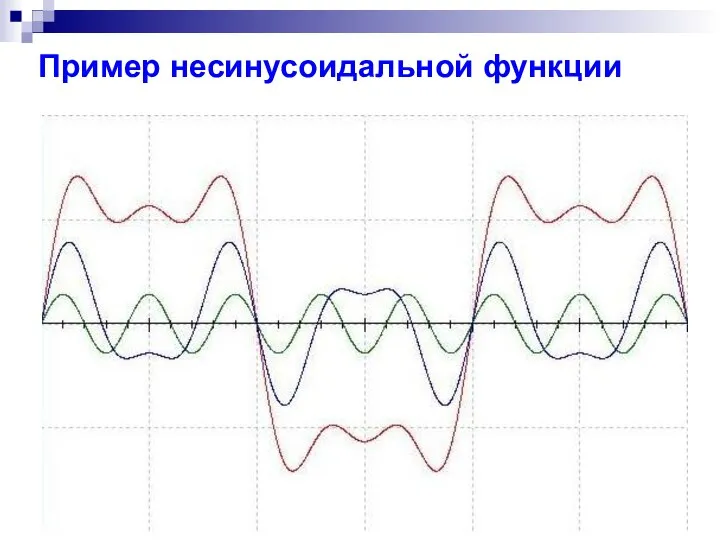
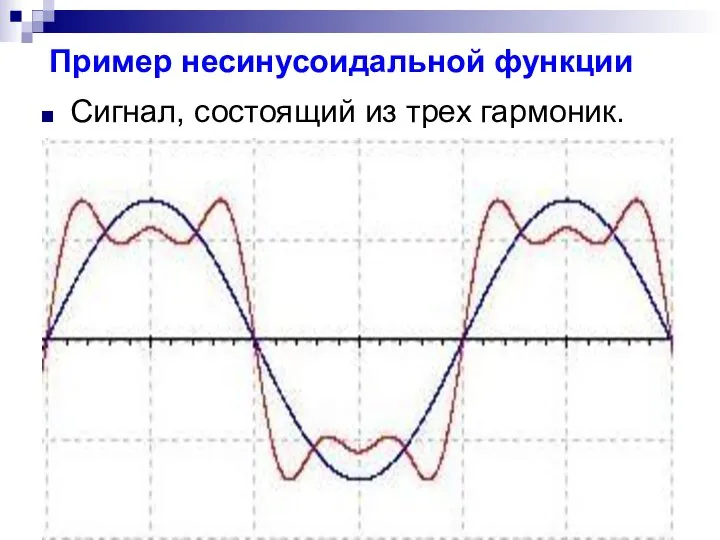
Пример несинусоидальной функции

Пример несинусоидальной функции
Сигнал, состоящий из трех гармоник.

Величины, характеризующие несинусоидальные токи
Максимальное значение – I max
Действующее значение
Среднее по модулю значение
Среднее за период значение
(постоянная составляющая)

Величины, характеризующие несинусоидальные токи
Коэффициент амплитуды
Коэффициент формы
Коэффициент искажений
Коэффициент гармоник

Величины, характеризующие несинусоидальные токи
Действующим значением периодической несинусоидальной переменной называется среднеквадратичное за период значение величины:

Величины, характеризующие несинусоидальные токи
На практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.

Мощность в цепях периодического несинусоидального тока
Допустим, ток и напряжение являются периодическими несинусоидальными функциями:

Мощность в цепях периодического несинусоидального тока
Среднее за период значение произведения синусоидальных функций различной частоты равно нулю, тогда
Где
Реактивная
мощность

Полная мощность
где Т – мощность искажений, определяемая произведениями действующих значений разнопорядковых гармонических тока и напряжения.
Мощность в цепях периодического несинусоидального тока

Электротехника и электроника
Рекомендуемая литература
1. Алтунин Б.Ю., Панкова Н.Г. Теоретические основы электротехники:
Комплекс учебно - методических материалов: Часть 1 / Б.Ю. Алтунин,
Н.Г. Панкова; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2007.-130 с.
2. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс учебно-методических материалов: Ч.1/ Б.Ю. Алтунин, А.А. Кралин; НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2007.-98 с.
3. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс учебно-методических материалов: Ч.2/ Б.Ю. Алтунин, А.А. Кралин; НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2008.-98 с
4. Касаткин, А.С. Электротехника /А.С. Касаткин, М.В. Немцов.-М.: Энергоатомиздат, 2000.
5. Справочное пособие по основам электротехники и электроники /под. ред. А.В. Нетушила.-М.: Энергоатомиздат, 1995.
6. Манаев Е.И. Основы радиоэлектроники.-3-е изд., перераб. И доп.-М.: Радио и связь, 1990.-512 с.: ил.
7. Новожилов, О. П. Электротехника и электроника: учебник / О. П. Новожилов. – М.: Гардарики, 2008. – 653 с.