Quantum mechanics

Quantum Physics – introduction
Getting ‘into’ the atom
Late in the 19th century, physicists explained properties of matter with particle model, light with wave model. Classical physics, which was continuous, had no theoretical limits on size of matter or radiation. Mechanics and electromagnetism together seemed to be enough.
However…

Black-body radiation remained unexplained
All hot bodies radiate.
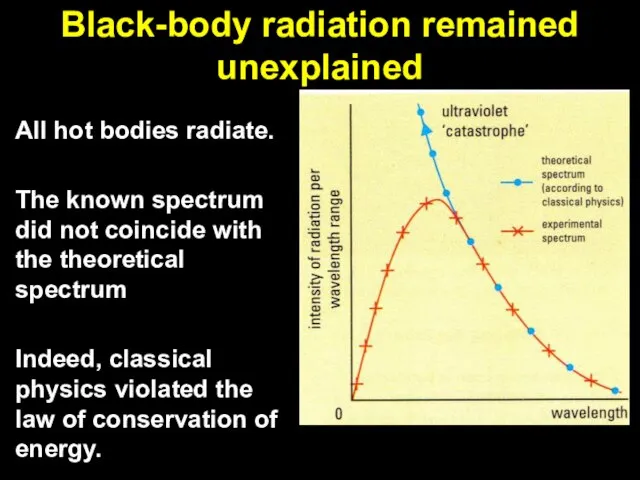
The known spectrum did not coincide with the theoretical spectrum
Indeed, classical physics violated the law of conservation of energy.

In 1900, Planck postulated that
All oscillators that emit radiation can only emit discrete energies. That is, radiation comes in packets or quanta (plural of quantum). These quanta are proportional to frequency:
E = hf
where h = 6.63 x 10-34 Js = 4.14 x 10-15 eV-s
h is known as “Planck’s constant”

Definition
What is one electronvolt?

Along comes Albert…
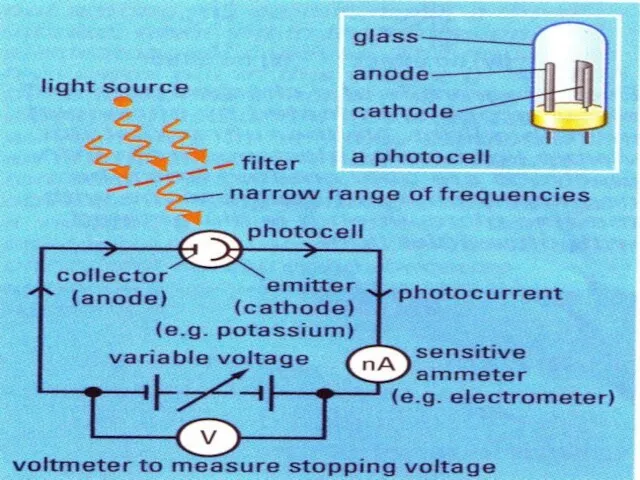
Photoelectric effect

Photoelectric effect

This equation explained
1) For each metal, there is a threshold frequency below which no electrons are emitted.
2) The number of electrons emitted is proportional to intensity of radiation.
3) Emitted electrons have KE up to a maximum value which depends on frequency of radiation*.
(* unexplained by classical physics)

For his work on
the photoelectric
Effect, Einstein
was awarded
the Nobel
Prize in 1921

Example 1
a) Find the longest wavelength beyond which no electrons are emitted from a caesium surface if Φcaesium = 1.80 eV.
b) If the surface is illuminated with monochromatic light of wavelength λ = 450 nm, calculate KEmax of emitted photoelectrons.
c) What is the stopping potential which just prevents photoemission in this situation?

De Broglie equation
During his PhD work, de Broglie proposed that electrons might behave as waves.

Electron diffraction
Using de Broglie equation for electrons accelerated through 1kV gives a wavelength of about _0.0388 nm_.
This is comparable to the wavelength of X-Rays.
Why are electrons easier to use than X-Rays when studying crystalline structures?

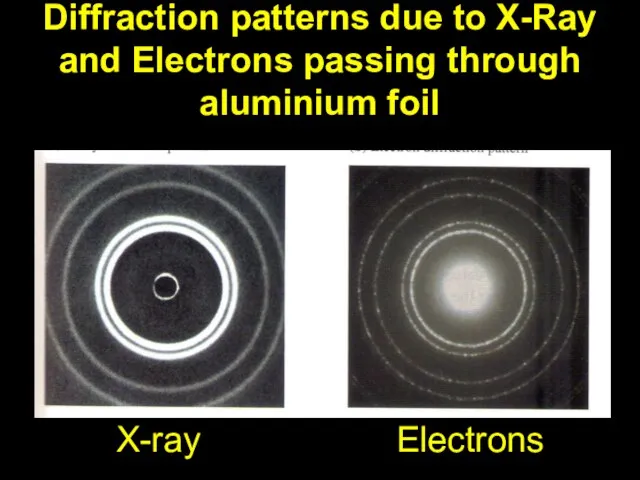
Diffraction patterns due to X-Ray and Electrons passing through aluminium foil
X-ray
Electrons

If all moving objects have an associated wave, why can’t we see the waves associated with buses?

Wave-particle duality
Sometimes light behaves like a wave, sometimes light behaves like a particle.
Wave-particle duality exists in the universe!
How accurately physical properties can be measured is limited.

Heisenberg’s uncertainty principle