Элементы комбинаторики

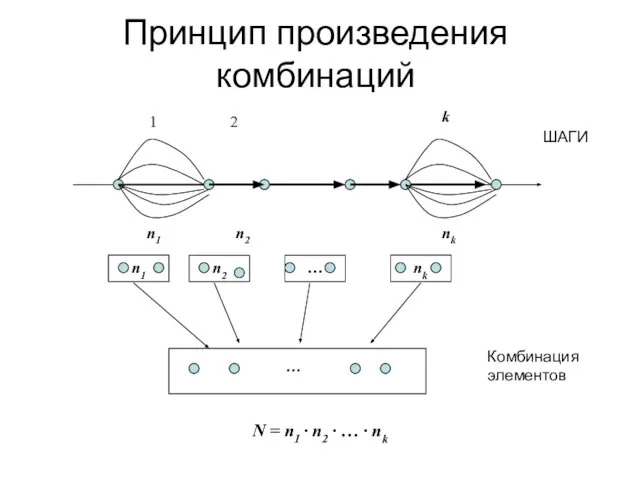
Принцип произведения комбинаций
N = n1 ∙ n2 ∙ … ∙ nk

Принцип произведения комбинаций
Пусть имеется k групп элементов, причем i-я группа содержит ni элементов, 1 ≤ i ≤ k.
Выберем из каждой группы по одному элементу.Тогда общее число N способов, которыми можно произвести такой выбор, равняется
N = n1 ∙ n2 ∙ … ∙ nk

Виды комбинаций
Перестановки
Размещения
Сочетания

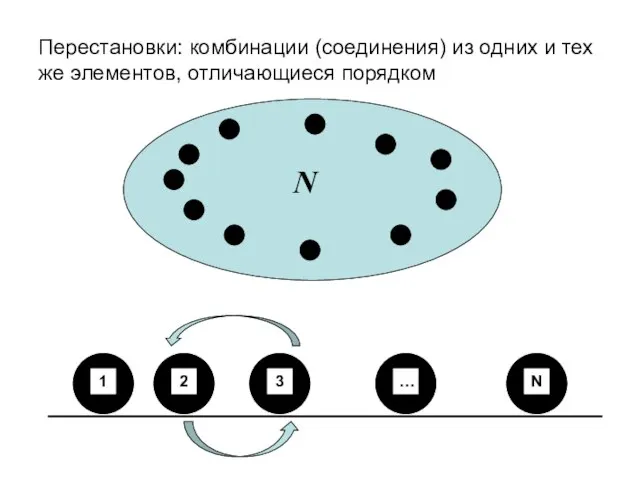
Перестановки: комбинации (соединения) из одних и тех же элементов, отличающиеся порядком

Подсчитаем число перестановок.
Используем принцип произведения комбинаций:

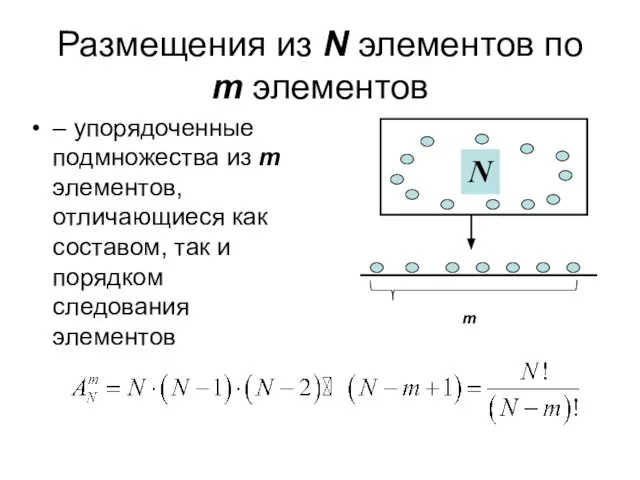
Размещения из N элементов по m элементов
– упорядоченные подмножества из m элементов, отличающиеся как составом, так и порядком следования элементов

Сочетания из N элементов по m элементов
– неупорядоченные подмножества из m элементов, отличающиеся только составом элементов.
Если в каждом сочетании произвести все возможные m! перестановок, то мы получим все размещения.
Число размещений и число сочетаний
Связаны соотношением:
Отсюда имеем:

Основное свойство сочетаний
Образование сочетаний связано с задачей разбиения множества N элементов на два подмножества так, что одно из них содержит m элементов, а другое – оставшиеся (N-m) элементов и является простейшим случаем более общей задачи о разбиении множества на k неупорядоченных подмножеств, содержащих n1, n2, … , nk элементов, причем n1 + n2 + … + nk = N.
Число таких комбинаций равно

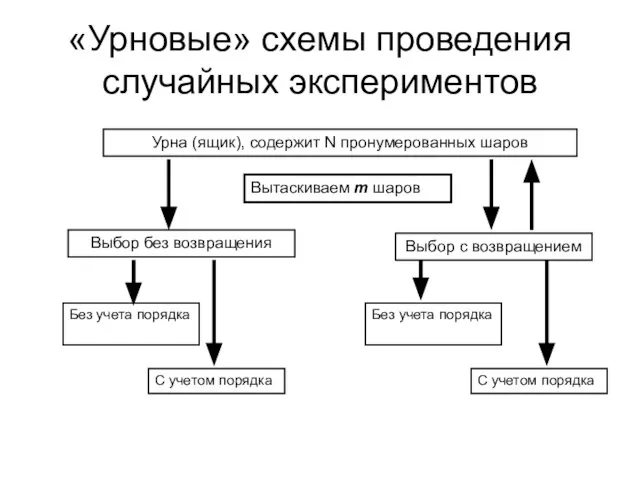
«Урновые» схемы проведения случайных экспериментов
Урна (ящик), содержит N пронумерованных шаров
Выбор с возвращением
Выбор без возвращения
Без учета порядка
Без учета порядка
С учетом порядка
С учетом порядка
Вытаскиваем m шаров

Выбор без возвращения с учетом порядка
Выбор без возвращения без учета порядка

Выбор с возвращением с учетом порядка
Общее количество выборок :
Выбор с возвращением без учета порядка
Два из двух