Элементы квантовой механики

12.1. Корпускулярно-волновая двойственность свойств частиц вещества

12.2. Соотношение неопределённостей
Только участием обеих щелей в прохождении электрона через диафрагму может быть объяснена возникающая на экране интерференционная картина. Любая попытка определить, через какую щель прошел электрон, неизбежно приводит к нарушению интерференции.
Двойственная корпускулярно-волновая природа микрочастиц накладывает ограничения на точность определения физических величин, характеризующих состояние частицы. Причем эти ограничения никак не связаны с точностью измерений, достижимой в конкретном эксперименте, а имеют принципиальное значение. Рассмотрим в качестве примера дифракцию электрона на щели.

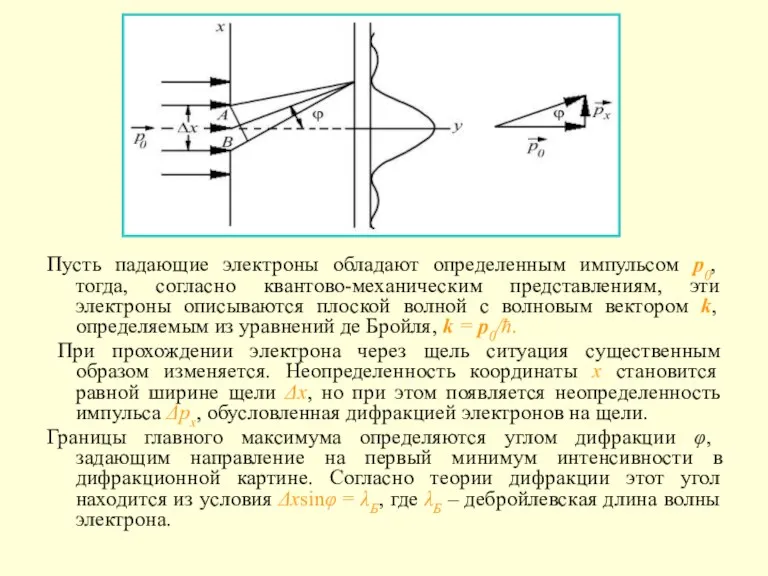
Пусть падающие электроны обладают определенным импульсом p0, тогда, согласно квантово-механическим представлениям, эти электроны описываются плоской волной с волновым вектором k, определяемым из уравнений де Бройля, k = p0/ħ.
При прохождении электрона через щель ситуация существенным образом изменяется. Неопределенность координаты x становится равной ширине щели Δx, но при этом появляется неопределенность импульса Δpx, обусловленная дифракцией электронов на щели.
Границы главного максимума определяются углом дифракции φ, задающим направление на первый минимум интенсивности в дифракционной картине. Согласно теории дифракции этот угол находится из условия Δxsinφ = λБ, где λБ – дебройлевская длина волны электрона.

Электроны, прошедшие через щель, в подавляющем большинстве случаев будут попадать в центральный дифракционный максимум. Границы главного максимума определяются углом дифракции φ1, задающим направление на первый минимум интенсивности в дифракционной картине. Согласно теории дифракции этот угол находится из условия Δxsinφ1 = λБ, где λБ – дебройлевская длина волны электрона. В силу малости угла φ sinφ ≈ tgφ, следовательно λБ/Δx = sinφ ≈ tgφ.
С другой стороны tgφ = px/py. Считая, что неопределенность Δpx проекции импульса вдоль оси x сравнима по порядку величины с px, получаем ΔxΔpx ≈ λБpy. Т.к. λБ = 2πħ/py, то ΔxΔpx ≈ 2πħ.
ΔrΔp ≥ ħ
Это соотношение было получено в 1927 г немецким физиком В. Гейзенбергом и называется соотношением неопределенностей Гейзенберга. Соотношение неопределенностей является математическим выражением принципа неопределенностей. Согласно этому принципу в природе не существует состояния частицы с точно определенными значениями координаты и проекции импульса на эту координатную ось.

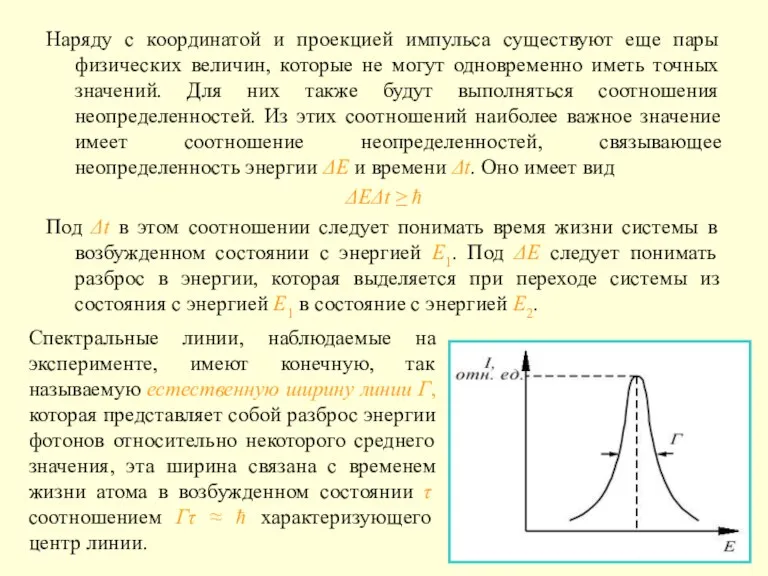
Наряду с координатой и проекцией импульса существуют еще пары физических величин, которые не могут одновременно иметь точных значений. Для них также будут выполняться соотношения неопределенностей. Из этих соотношений наиболее важное значение имеет соотношение неопределенностей, связывающее неопределенность энергии ΔE и времени Δt. Оно имеет вид
ΔEΔt ≥ ħ
Под Δt в этом соотношении следует понимать время жизни системы в возбужденном состоянии с энергией E1. Под ΔE следует понимать разброс в энергии, которая выделяется при переходе системы из состояния с энергией E1 в состояние с энергией E2.
Спектральные линии, наблюдаемые на эксперименте, имеют конечную, так называемую естественную ширину линии Г, которая представляет собой разброс энергии фотонов относительно некоторого среднего значения, эта ширина связана с временем жизни атома в возбужденном состоянии τ соотношением Гτ ≈ ħ характеризующего центр линии.

Измеряя на эксперименте естественную ширину спектральных линий Г, можно найти время жизни атома в том или ином возбужденном состоянии. Так, естественная ширина линии, измеренная в спектре атомов, излучающих в видимом диапазоне, составляет по порядку величины Г ~ 10-7 эВ. Тогда τ ≈ 10-8 с.
В квантовой механике теряет смысл деление полной энергии частицы на кинетическую и потенциальную. Кинетическая энергия Ек зависит от импульса частицы, а потенциальная энергия U – от ее координаты. Но поскольку, координата и импульс не могут одновременно иметь определенные значения, то полная энергия E, не может быть представлена в виде суммы одновременно точно определенных кинетической и потенциальной энергий. Таким образом, равенство
E = Ек + U
для мгновенных значений Ек и U в квантовой механике невозможно.
В дальнейшем будет показано, что это равенство оказывается справедливым для средних значений энергии
= <Ек> +
.

Невозможности состояния полного покоя микрочастицы.
Действительно, если область изменения координаты частицы ограничена, например,
Δх = а,
то, такая частица имеет разброс по импульсам
Δр ≥ ħ/а
и, следовательно, отличную от нуля энергию. Оценим по порядку величины минимальную энергию Emin, которой обладает частица.
Полагая, что
pmin ≈ Δpmin,
получаем
Emin = p2/2m ≈ ħ2/mа2.
Таким образом, частица в квантовой механике никогда не может находиться в состоянии полного покоя.

12.3. Уравнение Шредингера
Уравнение нерелятивистской квантовой механики, вывел в 1926 г. Э. Шредингер.
Общее не стационарное уравнение Шредингера, позволяющее определить в любой момент времени волновую функцию Ψ для частицы массы m0, находящееся в потенциальном поле U(x,y,z), имеет вид
Стандартным символом Δ обозначен дифференциальный оператор Лапласа, который в декартовой системе координат имеет вид
Уравнение в частных производных должно решаться с учетом определенных начальных и граничных условий на волновую функцию.
Начальное условие задает значение волновой функции в начальный момент времени t = 0.

Граничные условия являются следствием регулярности волновой функции, обеспечивая, в частности, ее непрерывность. Эти условия формулируются на границах областей, где потенциальная функция U терпит разрывы первого или второго рода. Сюда же относятся условия на волновую функцию в бесконечно удаленных точках пространства, которые обеспечивают выполнение условия нормировки.
Уравнение Шредингера, как и законы классической механики Ньютона, законы термодинамики, уравнения электродинамики Максвелла и другие основные физические уравнения, не может быть выведено из других соотношений. Его следует рассматривать как некоторое научное положение, справедливость которого доказывается согласием результатов расчетов, выполненных с помощью уравнения Шредингера, с данными экспериментов. Такое согласие установлено для большого числа явлений в атомной и ядерной физике. Квантовые эффекты, предсказанные с помощью уравнения Шредингера, лежат в основе многих технических устройств, приборов и технологий.
Непосредственной проверкой легко убедиться, что для свободной частицы, с кинетической энергий E = p2/2m0, движущейся в отсутствие силовых полей (U = 0) в направлении оси x, решением соответствующего уравнения Шредингера
является волновая функция
соответствующая плоской волне де Бройля.

Формально, малость длины волны де Бройля для частицы можно обеспечить, считая квант действия ħ некоторым параметром задачи и осуществляя предельный переход ħ→0 по этому параметру. Действительно, по формуле де Бройля при ħ→0 длина волны де Бройля также стремится к нулю. Поэтому переход от квантовой теории к классической в уравнении Шредингера можно осуществить, выполняя в нем предельный переход ħ→0. В курсах теоретической физики анализируются результаты такого предельного перехода и доказывается, что при ħ→0 общее временное уравнение Шредингера переходит в уравнение Гамильтона-Якоби классической механики.
Следует отметить, что с помощью волновых функций, найденных из решений уравнения Шредингера, можно описывать квантовые состояния только нерелятивистских частиц, которые движутся со скоростями, много меньшими скорости света в вакууме. Переход к релятивистским скоростям частиц в квантовой механике был впервые осуществлен для электрона П. Дираком в 1928 г. Такой переход потребовал принципиально новых физических идей для описания квантовых состояний релятивистских частиц, результатом применения которых явилось создание релятивистской квантовой механики. В основе этой теории лежит уравнение Дирака, которое обобщает уравнение Шредингера и в настоящее время широко используется в квантовой электродинамике и теории элементарных частиц.

12.4. Волновая функция и её статистический смысл
Состояние частицы в квантовой механике описывается заданием волновой функции Ψ(x,y,z,t), являющейся функцией пространственных координат и времени.
Аппарат, разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией Ψ, получать полную информацию о движении микрочастицы.
Невозможность задания состояния микрочастицы указанием в любой момент времени ее координат и скорости и отказ от траекторного способа описания движения приводит к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике, определяя состояние частицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени.
В 1926 г. М. Борн так сформулировал вероятностный смысл волновой функции в квантовой механике: Квадрат модуля волновой функции Ψ(x,y,z,t) определяет плотность вероятности w того, что в момент времени t ≥ 0 частица может быть обнаружена в точке пространства M = M(x,y,x) с координатами x, y и z.
Следовательно
w = dP/dV = |Ψ|2.

Отметим, что волновая функция в общем случае является комплекснй функцией, то есть содержит действительную и мнимую части. Физический смысл, поэтому, имеет не сама волновая функция, а ее квадрат модуля |Ψ|2 – действительная величина, которую во многих случаях удобно находить, умножая волновую функцию Ψ на комплексно сопряженную ей функцию Ψ*, так как из теории комплексных чисел следует, что (Ψ*Ψ) = |Ψ|2.
Тогда dP = |Ψ|2dV = (Ψ*Ψ)dV.
Здесь dP – вероятность того, что для заданного квантового состояния частицы в некоторый момент времени мы обнаружим частицу в элементарном объеме dV, окружающем точку M
В заданном квантовом состоянии частицы, описываемом волновой функцией Ψ(x,y,z,t), можно рассчитать также вероятность P того, что частица будет обнаружена в любой области пространства конечного объема V. Действительно, так как

Если в качестве области пространства взять все пространство, для которого V →∞, то обнаружение частицы во всем пространстве является достоверным событием, вероятность которого равна единице. Следовательно
Это есть условием нормировки волновой функции
Вероятностный смысл волновой функции накладывает на нее определенные ограничения.
1. Условие конечности волновой функции. Это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. Квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно.
3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции дΨ/дx, дΨ/дy и дΨ/дz..

Сформулируем одно из важных свойств квантовых состояний, которое формально является следствием линейности уравнения Шредингера для волновой функции, которое будет обсуждаться в следующем параграфе. Из линейности этого уравнения следует, что если частица может находиться в квантовом состоянии, описываемом волновой функцией Ψ1, а также в другом квантовом состоянии, описываемом волновой функцией Ψ2, то эта частица может также находиться в состоянии, описываемом волновой функцией Ψ = C1Ψ1 + C2Ψ2, где C1 и C2, в общем случае комплексные числа.
Очевидно, можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния частицы, которое описывается волновой функцией
В таком состоянии квадрат модуля коэффициента Cn определяет вероятность того, что при измерении, проведенном над системой с такой волновой функцией Ψ, мы обнаружим ее в квантовом состоянии, описываемом волновой функцией Ψn. Поэтому для нормированных волновых функций

12.5. Квантование энергии и момента импульса. Принцип суперпозиции
В работах М.Борна, П.Дирака и др. был сформулирован второй постулат квантовой механики, утверждающий, что каждой физической величине соответствует определенный оператор этой физической величины. При этом соотношения между операторами в квантовой механике имеют ту же структуру, что и соотношения между соответствующими им физическими величинами в классической механике.
Оператор - это математическое правило, следуя которому мы можем преобразовать одну функцию в другую. Задать оператор - это означает определить рецепт такого преобразования. Такое преобразование может быть простым умножением исходной функции на число или известную функцию, дифференцированием функции, перестановкой аргументов функции и др.
В квантовой механике в качестве символа соответствующего оператора используется классическое обозначение физической величины, ставя над буквой «шляпку» в виде значка «^».
Оператор предполагается действующим на написанную вслед за ним функцию. В качестве таких функций в квантовой механике выступают волновые функции.

1. Оператор координаты. Действие этого оператора на волновую функцию сводится к умножению ее на соответствующую координату, то есть.
2. Оператор импульса. С помощью операций дифференцирования по координатам определим операторы проекций импульса, записав эти определения в символической операторной форме как
3. Оператор момента импульса. По формуле классической механики, определяющей момент импульса частицы как вектор L = [rxp], запишем выражения для его проекций на координатные оси и превратим в операторные, определяющие операторы проекций момента импульса:

Задачи квантовой механики, обладающие сферической симметрией, удобнее решать не в декартовой, а в сферической системе координат r, θ и φ. Переходя от декартовых координат к сферическим по обычным правилам замены переменных x = rsinθcosφ, y = rsinθsinφ, z = rcosθ, тогда
4. Операторы энергий. Классическая формула связи кинетической энергии частицы с квадратом ее импульса Eк = p2/2m0 позволяет записать аналогичное соотношение между соответствующими операторами. Поэтому
Так как полная энергия частицы в классической механике есть сумма кинетической и потенциальной энергий, то в квантовой механике оператор полной энергии определяется как сумма операторов кинетической и потенциальной энергий. Поэтому

Спектр собственных значений операторов
Спектр собственных значений оператора координаты непрерывен.
2. Спектр оператора проекции импульса также является непрерывным спектром.
3. Примером дискретного спектра является спектр собственных значений оператора проекции момента импульса . Для определения этого спектра направим полярную ось сферической системы координат вдоль направления оси z. Тогда
Так как угловая координата φ является циклической переменной задачи, то условие однозначности собственной функции сводится к условию ее периодичности: Ψ(φ + 2π) = Ψ(φ)
из условия нормировки

4. Для того, чтобы найти собственные функции и собственные значения оператора квадрата момента импульса возьмем уравнение
спектр собственных значений оператора оказывается дискретным
Каждому собственному значению соответствует 2l + 1 различных собственных функций, которые выделяются заданием целочисленного параметра m = 0, ±1, ±2, …,±l.
Собственные функции оператора , имеют вид Ψl,m = Yl,m(θ,φ).
Функции Yl,m относятся к классу специальных функций и называются сферическими или шаровыми функциями. Если их нормировать условием
то можно выписать несколько первых нормированных сферических функций в явном виде

Одновременное измерение разных физических величин
Важным вопросом в квантовой механике является вопрос о возможности одновременного точного измерения в некоторой квантовой системе двух различных физических величин.
Физические величины a и b будут одновременно точно измеримы только в том случае, если соответствующие им операторы и имеют общую систему собственных функций
Если две разные физические величины a и b могут быть одновременно точно измерены, то соответствующие им операторы и должны быть коммутирующими операторами
Обратно, некоммутативность операторов указывает на невозможность такого одновременного точного измерения двух соответствующих им физических величин.
Можно ли одновременно точно измерить координату x частицы и проекцию px ее импульса?

Уравнение Шредингера для стационарных состояний
Основным уравнением нерелятивистской квантовой механики является временное уравнение Шредингера
Если U(x,y,z,t) = U(x,y,z), то такие силовые поля называются стационарными силовыми полями.
Найдем общий вид волновой функции, соответствующей стационарному состоянию Ψ(x,y,z,t) = ψ(x,y,z)φ(t)
Это уравнение называется уравнением Шредингера для стационарных состояний. Часто уравнение Шредингера для стационарных состояний записывают в следующей форме

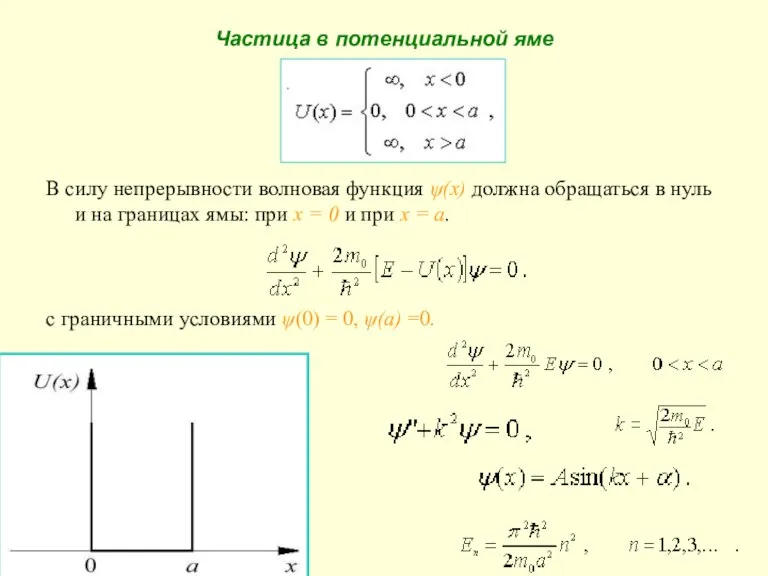
Частица в потенциальной яме
В силу непрерывности волновая функция ψ(x) должна обращаться в нуль и на границах ямы: при x = 0 и при x = a.
с граничными условиями ψ(0) = 0, ψ(a) =0.

Число n, определяющее энергию частицы в яме, называется квантовым числом, а соответствующее ему значение En – уровнем энергии. Состояние частицы с наименьшей энергией, в данном случае с n = 1, называется основным состоянием.
Следует отметить, что минимальное значение энергии частицы, находящейся в основном состоянии, отлично от нуля. Этот результат согласуется с соотношением неопределенностей и является общим для всех задач квантовой механики.

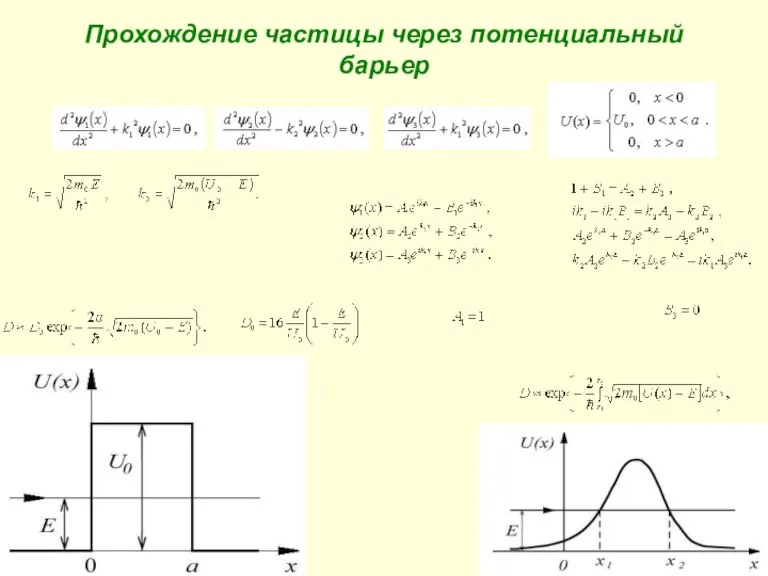
12.6. Прохождение частицы через потенциальный барьер
Движение частицы в области потенциального порога

Рассмотрим случай, когда энергия налетающей на порог частицы E превышает высоту потенциального порога U0, т.е. E > U0. Такой порог носит название низкого потенциального порога. В этом случае уравнение Шредингера для областей I и II имеет вид

Прохождение частицы через потенциальный барьер

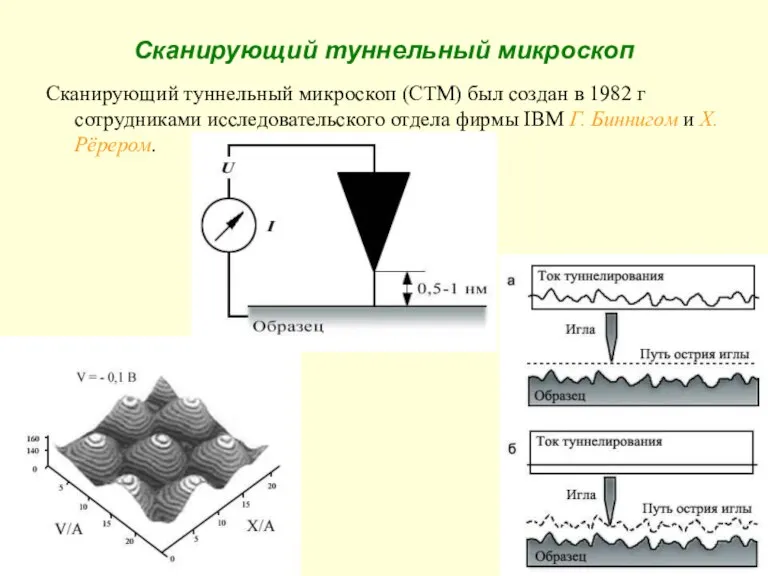
Сканирующий туннельный микроскоп
Сканирующий туннельный микроскоп (СТМ) был создан в 1982 г сотрудниками исследовательского отдела фирмы IBM Г. Биннигом и Х. Рёрером.

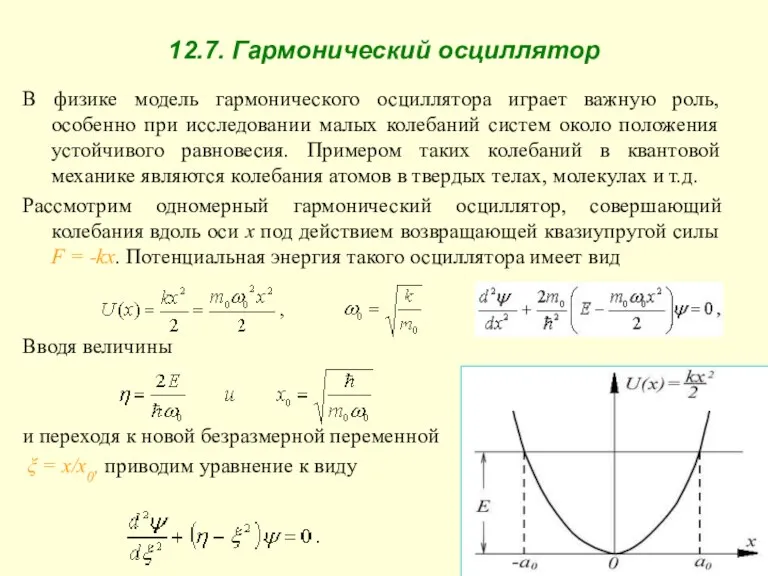
12.7. Гармонический осциллятор
В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д.
Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси x под действием возвращающей квазиупругой силы F = -kx. Потенциальная энергия такого осциллятора имеет вид
Вводя величины
и переходя к новой безразмерной переменной
ξ = x/x0, приводим уравнение к виду

Анализ показывает, что волновые функции, являющиеся решением уравнения, будут непрерывными и конечными не при всех значениях параметра η, а лишь при η = 2n + 1, n = 1, 2, 3,…
Выражая, энергию осциллятора E через η, получаем
En = ћω0(n + ½), n = 0, 1, 2, 3,…
Это соотношение и определяет закон квантования энергии гармонического осциллятора. Энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии ΔE = ћω0 друг от друга.
При значение квантового числа n = 0 имеет место так называемые нулевые колебания – колебаний с энергией E0 = ћω0/2.
Нулевые колебания играют в физике весьма важную роль, в частности они
обусловливают отсутствие кристаллизации
жидкого гелия при нормальном давлении
даже при абсолютном нуле температур.

Эквидистантность энергетических уровней гармонического осциллятора на первый взгляд означает, что осциллятор может поглощать и испускать излучение с частотой ω, кратной ω0, т.е. ω = Δnω0, где Δn – разность квантовых чисел начального и конечного уровней осциллятора. Однако, на самом деле это не так. Точный расчет, выходящий за рамки данного курса, показывает, что особенности испускания и поглощения электромагнитного излучения гармоническим осциллятором таковы, что возможны переходы только между соседними уровнями, т.е. Δn = ±1.
Перейдем теперь к анализу волновых функций гармонического осциллятора. Как показано в теории дифференциальных уравнений с переменными коэффициентами, волновые функции, являющиеся решениями уравнения, имеют вид
где Hn(ξ) – полином Чебышева-Эрмита n-го порядка, определяемый выражением