Содержание
- 2. ТЕМА ЛЕКЦИИ: «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ» © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 3. СОДЕРЖАНИЕ ЛЕКЦИИ 1. ПОНЯТИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ 2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦЫ 3. ОПЕРАЦИИ
- 4. 1. ПОНЯТИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 5. ОПРЕДЕЛЕНИЯ МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЕЕ ЭЛЕМЕНТАМИ © Фролова Ю.Б.
- 6. ВИДЫ МАТРИЦ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 7. 2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦЫ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 8. НУМЕРАЦИЯ СТРОК И СТОЛБЦОВ СТРОКИ НУМЕРУЮТСЯ СВЕРХУ ВНИЗ, НАЧИНАЯ С № 1 СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА НАПРАВО,
- 9. СТРОКА И СТОЛБЕЦ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 10. РАЗМЕР МАТРИЦЫ МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ РАЗМЕРНОСТИ m НА n ©
- 11. ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРНОСТИ m НА n © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 12. ЭЛЕМЕНТ МАТРИЦЫ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 13. ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 14. ТРЕУГОЛЬНЫЕ МАТРИЦЫ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 15. 3. ОПЕРАЦИИ НАД МАТРИЦАМИ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 16. УМНОЖЕНИЕ НА ЧИСЛО ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО: © Фролова Ю.Б. Воронежский государственный педагогический университет,
- 17. СЛОЖЕНИЕ И ВЫЧИТАНИЕ МАТРИЦ МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ: © Фролова Ю.Б. Воронежский государственный
- 18. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 19. УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ) © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 20. УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ: © Фролова Ю.Б. Воронежский государственный
- 21. УМНОЖЕНИЕ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА
- 22. ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
- 23. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 24. ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 25. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ A•E=E•A=A © Фролова Ю.Б. Воронежский государственный педагогический университет, 2011
- 27. Скачать презентацию
























 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)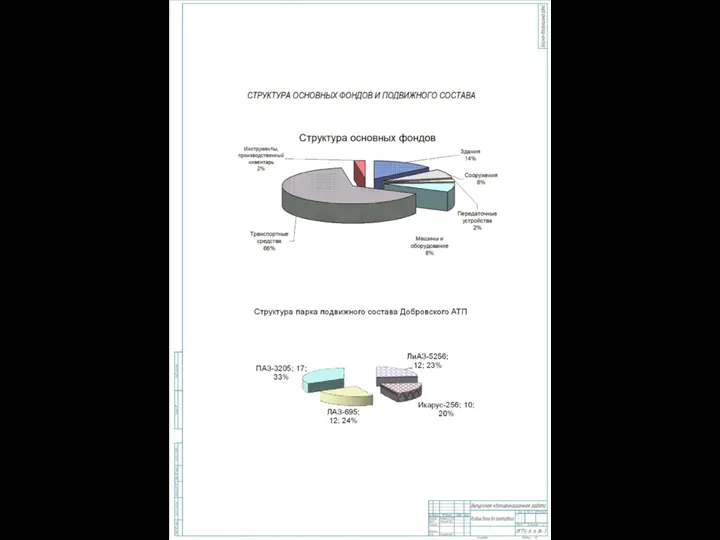 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС