Эллипс

Эллипс и его уравнение.
Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная (и большая, чем расстояние между фокусами).

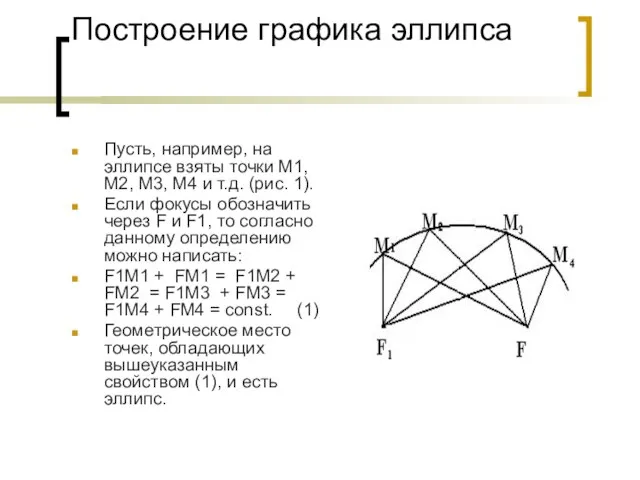
Построение графика эллипса
Пусть, например, на эллипсе взяты точки M1, M2, M3, M4 и т.д. (рис. 1).
Если фокусы обозначить через F и F1, то согласно данному определению можно написать:
F1M1 + FM1 = F1M2 + FM2 = F1M3 + FM3 = F1M4 + FM4 = const. (1)
Геометрическое место точек, обладающих вышеуказанным свойством (1), и есть эллипс.

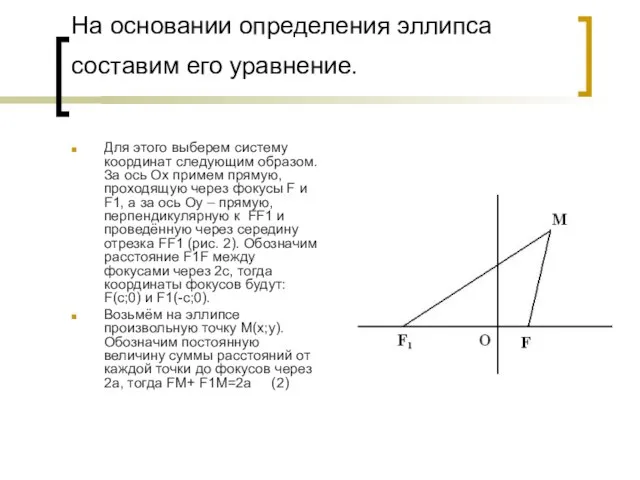
На основании определения эллипса составим его уравнение.
Для этого выберем систему координат следующим образом. За ось Ox примем прямую, проходящую через фокусы F и F1, а за ось Oy – прямую, перпендикулярную к FF1 и проведённую через середину отрезка FF1 (рис. 2). Обозначим расстояние F1F между фокусами через 2с, тогда координаты фокусов будут: F(с;0) и F1(-с;0).
Возьмём на эллипсе произвольную точку M(x;y). Обозначим постоянную величину суммы расстояний от каждой точки до фокусов через 2а, тогда FM+ F1M=2а (2)

По формуле расстояний между двумя точками найдём:
FM= √(x-с)²+(y-0)²=√(x-с)²+y²,
F1M= √(x+с)²+(y-0)²=√(x+с)²+y²
Теперь равенство (2) перепишется следующим образом:
√(x-с)²+y² + √(x+с)²+y²=2а (3)
и будет представлять уравнение эллипса в принятой системе координат.
Упростим уравнение (3).
Уравнение эллипса

Для этого перенесём один из радикалов в правую часть уравнения: √(x-с)²+y²=2а-√(x+с)²+y².
Возведём обе части этого равенства в квадрат:
(x-с)²+y²=4а²-4а√(x+с)²+y²+(x+с)²+y².
Раскроем скобки: х²-2сх+с²+у²=4а²-4а√х²+2сх+с²+у²+х²+2сх+с²+у²
Приведём подобные члены: -2сх=4а²-4а√х²+2сх+с²+у²+2сх,
4а√х²+2сх+с²+у²=4а²+4сх.

Сократив на 4 и снова возведя в квадрат обе части равенства, получим:
а² (х²+2сх+с²+у²)=(а²+сх)²,
или
а²х²+2а²сх+а²с²+а²у²=а4+2а²сх+с²х².
Перенесём все члены, содержащие х и у, в левую часть равенства, остальные члены - в правую:
а²х²+с²х²+а²у²=а-а²с²,
или
(а²-с²)х²+а²у²=а²(а²-с²). (4)

Но согласно определению эллипса 2с<2а, отсюда с<а.
Из последнего неравенства следует, что а²-с²>0, а потом эту разность можно обозначить через b². Поставив это обозначение в равенство (4), найдём:
b²x²+a²y²=a²b². (5)
Наконец, разделим все члены последнего равенства на a²b²; окончательно получим: х²/а²+у²/b²=1 (6),
где b²=а²-с². (7)
Уравнение (6) и есть простейший вид уравнения эллипса.

Исследование уравнений эллипса.
Определим сначала у из уравнения (5):
откуда
Из этого же уравнения (5) найдём:
следовательно,

Исследование симметричности эллипса в системе координат
Пусть │х│< а. Тогда под корнем в равенстве (1) получится положительное число, а поэтому у будет иметь два значения, равные по абсолютной величине, но с противоположными знаками. Это значит, что каждому значению х соответствуют две точки эллипса, симметричные относительно оси Ох.
Пусть теперь │у│< b.
Тогда каждому значению у, как мы видим из равенства (2), отвечают два значения х, равные по абсолютной величине, но с разными знаками. Отсюда следует, что каждому значению у соответствуют на эллипсе две точки, симметричные относительно оси Оу.
Из сказанного заключаем: эллипс симметричен относительно координатных осей.

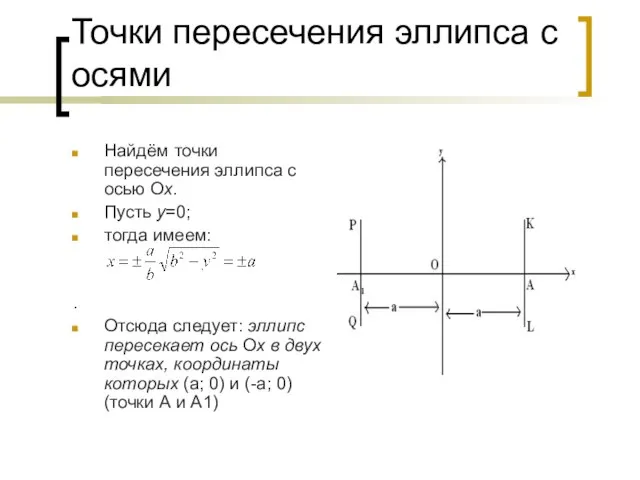
Точки пересечения эллипса с осями
Найдём точки пересечения эллипса с осью Ох.
Пусть у=0;
тогда имеем:
.
Отсюда следует: эллипс пересекает ось Ох в двух точках, координаты которых (а; 0) и (-а; 0) (точки А и А1)

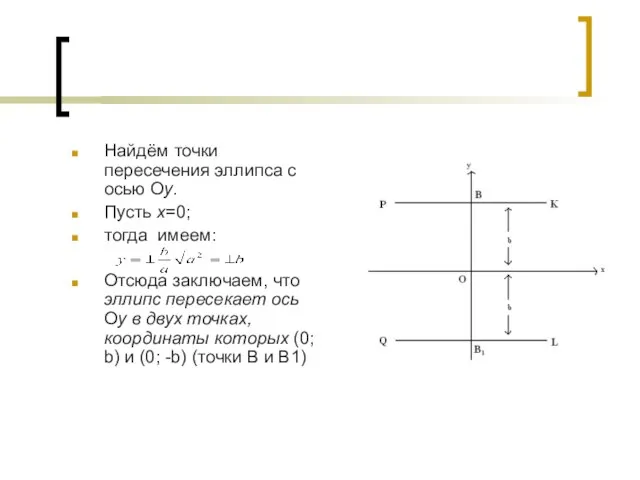
Найдём точки пересечения эллипса с осью Оу.
Пусть х=0;
тогда имеем:
Отсюда заключаем, что эллипс пересекает ось Оу в двух точках, координаты которых (0; b) и (0; -b) (точки В и В1)

Ограниченность эллипса
Пусть х принимает такие значения, что │х│>а;
тогда выражение под корнем в равенстве
будет отрицательным, и, следовательно, у будет иметь мнимые значения. А это значит, что не существует точек эллипса, абсциссы которых удовлетворяют условию , т.е. эллипс заключён между прямыми х= +а и х= - а (см. рис.3, прямые KL и PQ).
Если же положить │у│> b,
то аналогично получим для х мнимые значения. Это говорит о том, что точки, удовлетворяющие условию, на эллипсе не лежат, т.е. эллипс заключён между прямыми у= +b и у= -b ().

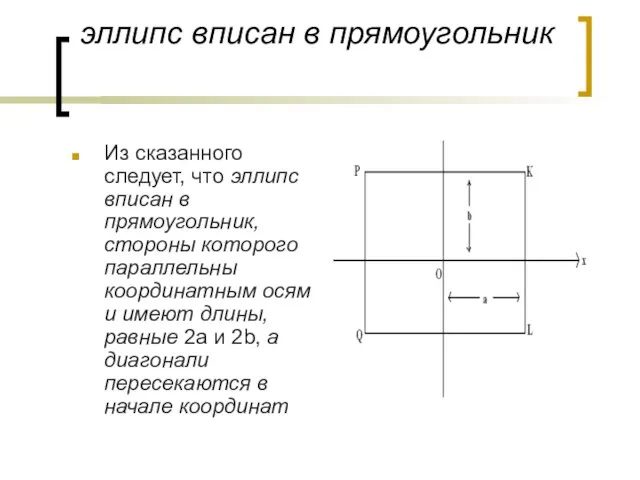
эллипс вписан в прямоугольник
Из сказанного следует, что эллипс вписан в прямоугольник, стороны которого параллельны координатным осям и имеют длины, равные 2а и 2b, а диагонали пересекаются в начале координат

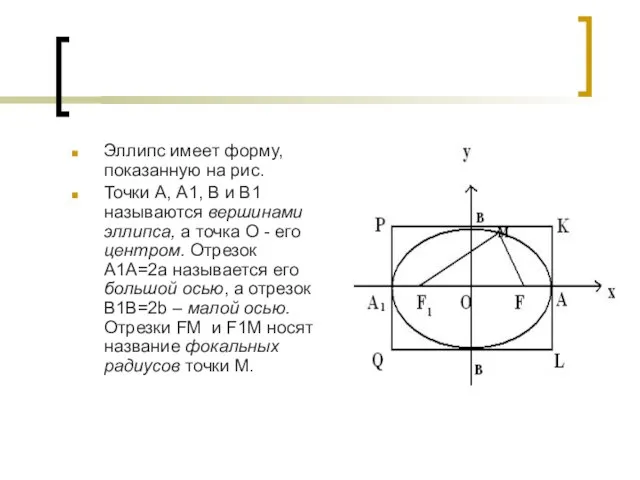
Эллипс имеет форму, показанную на рис.
Точки А, А1, В и В1 называются вершинами эллипса, а точка О - его центром. Отрезок А1А=2а называется его большой осью, а отрезок В1В=2b – малой осью. Отрезки FM и F1M носят название фокальных радиусов точки М.

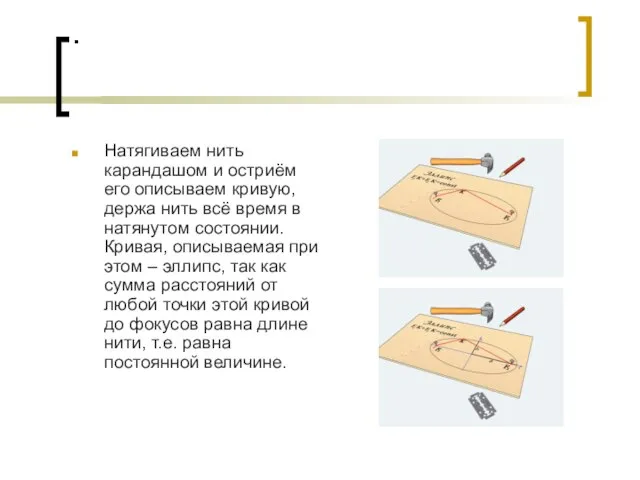
Практическое построение эллипса
Пользуясь определением эллипса, его легко построить непрерывным движением карандаша Для этого берём нерастяжимую нить длиной, равной большой оси эллипса, т.е. длиной 2а, и закрепляем концы этой нити в фокусах, положение которых предполагается известным.

.
Натягиваем нить карандашом и остриём его описываем кривую, держа нить всё время в натянутом состоянии. Кривая, описываемая при этом – эллипс, так как сумма расстояний от любой точки этой кривой до фокусов равна длине нити, т.е. равна постоянной величине.