массой 8 кг под углом 60° к горизонту со скоростью 5 м/с. Какую скорость приобретет мальчик?
1) 5,8 м/с 2)1,36 м/с 3) 0,8 м/с 4) 0,4 м/с
А2 Человек , равномерно поднимая веревку, достал ведро из колодца глубиной 10м. Масса ведра – 1,5 кг, масса воды в ведре – 10 кг. Какова работа силы упругости?
1) 1150 Дж 2) 1300 Дж 3) 1000 Дж 4) 850 Дж
А3 Человек тянет брусок массой 1 кг по горизонтальной поверхности с постоянной скоростью, действуя на него в горизонтальном направлении. Коэффициент трения между бруском и поверхностью µ= 0,1. Скорость движения бруска 10 м/с. Какую мощность развивает человек, перемещая груз?
1) 0,1 Вт 2) 100 Вт 3) 0 4) 10 Вт
А4 При выстреле из пружинного пистолета вертикально вверх шарик массой 100 г поднимается на высоту 2м. Какова жесткость пружины, если до выстрела она была сжата на 5 см?
1) 2000Н/м 2) 1600Н/м 3) 800Н/м 4) 250Н/м
Решите самостоятельно









 Контрольний норматив. Тести і нормативи оцінки фізичної підготовленості студентів
Контрольний норматив. Тести і нормативи оцінки фізичної підготовленості студентів Inventions. Text provided by ukurcheev bogdan
Inventions. Text provided by ukurcheev bogdan Подходы к управлению
Подходы к управлению Колледж бодибилдеров
Колледж бодибилдеров Географические координаты
Географические координаты Презентация на тему Частушки
Презентация на тему Частушки СКАЗКА
СКАЗКА Проект «Первая помощь при переломах, вывихах и растяжении связок»
Проект «Первая помощь при переломах, вывихах и растяжении связок» Виртуальные машины
Виртуальные машины Презентация на тему "Формирование учебной мотивации у младших школьников" - скачать презентации по Педагогике
Презентация на тему "Формирование учебной мотивации у младших школьников" - скачать презентации по Педагогике Профессиональный клуб учителей
Профессиональный клуб учителей Сувенирная мастерская, 2 год обучения
Сувенирная мастерская, 2 год обучения БГТУ ВОЕНМЕХ им. Д.Ф. Устинова
БГТУ ВОЕНМЕХ им. Д.Ф. Устинова Пророки
Пророки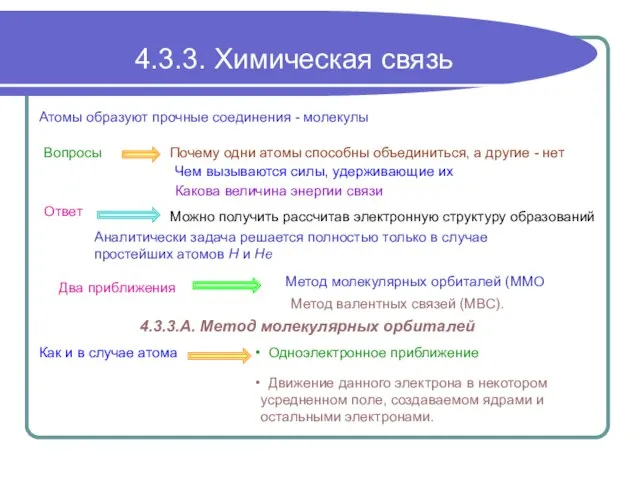 4.3.3. Химическая связь
4.3.3. Химическая связь Тема урока:Сделки и представительство.
Тема урока:Сделки и представительство. Мои пробабушка и продедушка
Мои пробабушка и продедушка Презентация на тему Изобразительное искусство классицизма и рококо
Презентация на тему Изобразительное искусство классицизма и рококо Проектирование блочной котельной
Проектирование блочной котельной Презентация на тему Характеристика стран ОПЕК
Презентация на тему Характеристика стран ОПЕК  Тренинг-семинар Твой характер – в твоих руках
Тренинг-семинар Твой характер – в твоих руках Мастер-класс Цветочное панно
Мастер-класс Цветочное панно Мастер-класс на тему: Мозаика из яичной скорлупы
Мастер-класс на тему: Мозаика из яичной скорлупы Соматоформды бұзылыстар
Соматоформды бұзылыстар Взаимодействие аллельных генов. Кодомирование
Взаимодействие аллельных генов. Кодомирование День Святого Валентина
День Святого Валентина IT-лицей Казанского федерального университета
IT-лицей Казанского федерального университета ПЕРИОДЫ ДЕТСКОГО ВОЗРАСТА. ЗНАЧЕНИЕ ГЕНЕТИЧЕСКИХ И НАСЛЕДСТВЕННЫХ факторов
ПЕРИОДЫ ДЕТСКОГО ВОЗРАСТА. ЗНАЧЕНИЕ ГЕНЕТИЧЕСКИХ И НАСЛЕДСТВЕННЫХ факторов