Содержание
- 2. «В мире нет места для некрасивой математики» Г. Харди «Все есть число» Пифагор
- 3. Гипотеза исследования: Выкладывая различные правильные многоугольники, мы получаем разные классы многоугольных чисел. Предположительно от фигурных чисел
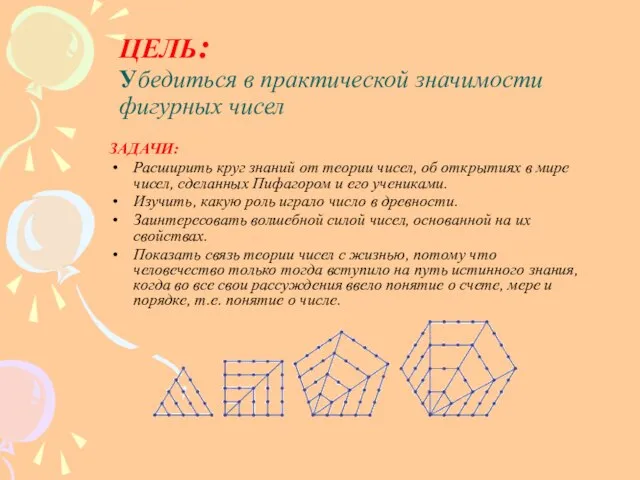
- 4. ЦЕЛЬ: Убедиться в практической значимости фигурных чисел ЗАДАЧИ: Расширить круг знаний от теории чисел, об открытиях
- 5. Из истории: Еще задолго до нашей эры ученые, комбинируя натуральные числа, составили из них затейливые ряды,
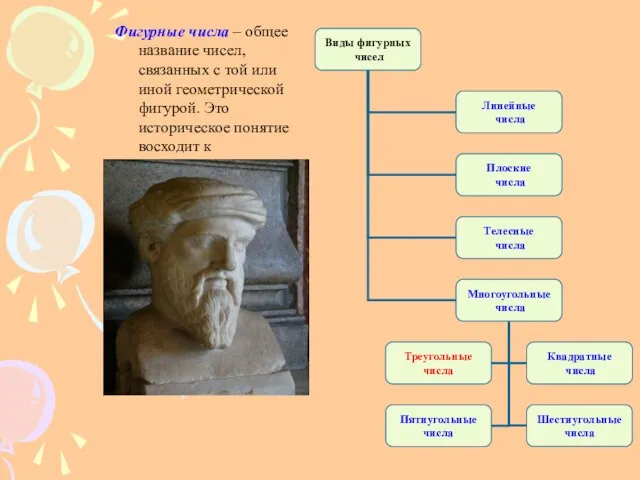
- 6. Фигурные числа – общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие
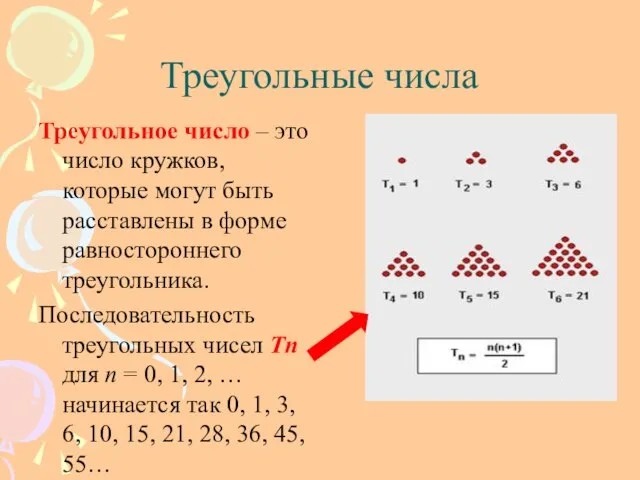
- 7. Треугольные числа Треугольное число – это число кружков, которые могут быть расставлены в форме равностороннего треугольника.
- 8. Какой же вид имеют треугольные числа? Заметим, что 1 = 1 3 = 1 + 2
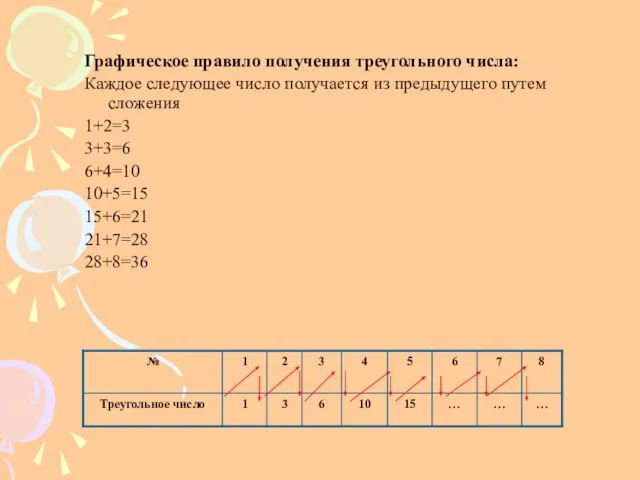
- 9. Графическое правило получения треугольного числа: Каждое следующее число получается из предыдущего путем сложения 1+2=3 3+3=6 6+4=10
- 10. Кроме треугольных чисел существуют также числа квадратные, пятиугольные, шестиугольные и т. п. Они связаны соответственно с
- 11. Решение примера! Чему равно треугольное число с номером 35? ½*35*(35+1)=1/2*35*36=630 Чему равно треугольное число с номером
- 12. А вы решите? Задача: Шары уложили в равносторонний треугольник, в котором 25 рядов. Сколько потребовалось шаров?
- 13. Используемая литература Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона http://dic.academic.ru/contents.nsf/brokgauz_efron/ Задачи на смекалку: Учебник для 5
- 15. Скачать презентацию








 Презентация на тему Предложения с вводными конструкциями (8 класс)
Презентация на тему Предложения с вводными конструкциями (8 класс) Салон красоты De’Paris. Издержки
Салон красоты De’Paris. Издержки ВЛАСТЬ и НАРОД в сатире М.Е.Салтыкова-Щедрина «История одного города»
ВЛАСТЬ и НАРОД в сатире М.Е.Салтыкова-Щедрина «История одного города» The system of State bodies of India
The system of State bodies of India Генерация идей и оценка их привлекательности
Генерация идей и оценка их привлекательности ГИПЕРЛИПИДЕМИЯ
ГИПЕРЛИПИДЕМИЯ  Семья и школа
Семья и школа Электронное портфолиоили Персональный сайт учителя
Электронное портфолиоили Персональный сайт учителя ВиртуализацияMicrosoft Application Virtualization 4.6(ранее SoftGrid)Демонстрация.
ВиртуализацияMicrosoft Application Virtualization 4.6(ранее SoftGrid)Демонстрация. Технологическое оборудование
Технологическое оборудование Шаблон проекта
Шаблон проекта Переформулировки поисковых запросов в Яндексе
Переформулировки поисковых запросов в Яндексе Чершкало Светлана Сергеевна
Чершкало Светлана Сергеевна Презентация на тему Малайзия (малайск. Malaysia)
Презентация на тему Малайзия (малайск. Malaysia) 点击添加相关文字内容
点击添加相关文字内容 Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Задачи по теме
Задачи по теме Новогодние игрушки и поделки (2 часть)
Новогодние игрушки и поделки (2 часть) Методические особенности развития прыгучести у волейболистов
Методические особенности развития прыгучести у волейболистов .
. Пирĕн тăрăхри йывăçсем
Пирĕн тăрăхри йывăçсем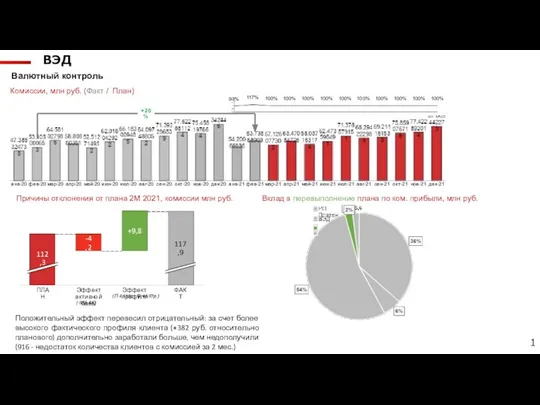 Валютный контроль
Валютный контроль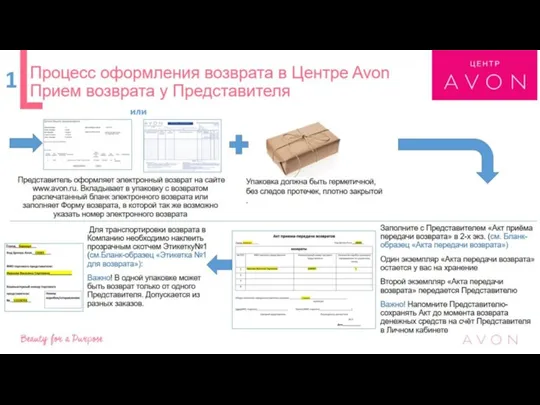 Прием возвратов у представителя в центре Avon
Прием возвратов у представителя в центре Avon Параолимпийцы Оренбургской области
Параолимпийцы Оренбургской области Презентация на тему Оптика Атомная и ядерная физика
Презентация на тему Оптика Атомная и ядерная физика Вироби зі скла. Сходи
Вироби зі скла. Сходи Алан Милн
Алан Милн Я - иллюстратор детских книг
Я - иллюстратор детских книг