Функция

Содержание
Понятие функции
Способы задания функции
Область определения функции и область задания функции

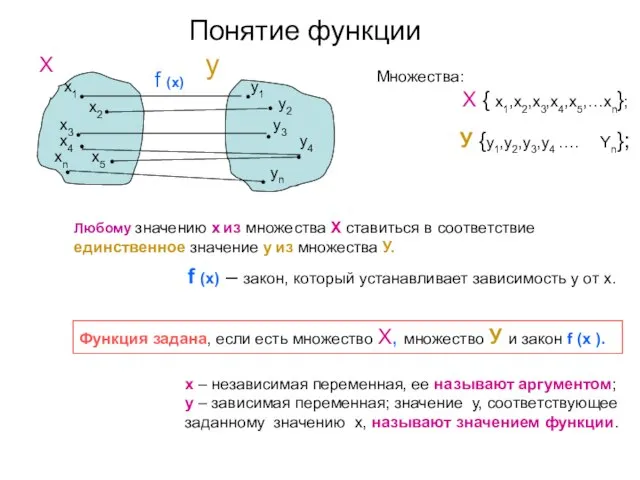
Понятие функции
y
X
•
•
x1
y1
•
•
x2
y2
x3
•
•
•
x4
y3
•
•
x5
y4
•
•
xn
yn
f (х)
Множества:
X { x1,x2,x3,x4,x5,…xn};
У {y1,y2,y3,y4 …. Yn};
Любому значению х из множества Х ставиться в соответствие единственное значение у из множества У.
f (х) – закон, который устанавливает зависимость у от х.
Функция задана, если есть множество Х, множество У и закон f (x ).
х – независимая переменная, ее называют аргументом; у – зависимая переменная; значение у, соответствующее заданному значению х, называют значением функции.

Способы задания функции (1)
4.Символическое обозначение функции:
1.Закон f (x) может быть задан формулой:
2.Закон f (x) предписывает порядок выполнения действий c переменной х;
3.В таком случае говорят, что функция задана формулой;
5. Читается:
“эф от икс”,“игрек от икс”,“игрек”

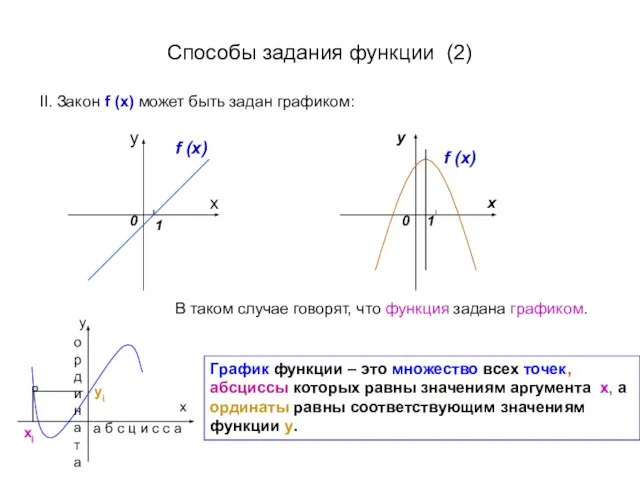
Способы задания функции (2)
II. Закон f (x) может быть задан графиком:
x
f (x)
f (x)
В таком случае говорят, что функция задана графиком.
График функции – это множество всех точек, абсциссы которых равны значениям аргумента х, а ординаты равны соответствующим значениям функции y.
ордината
а б с ц и с с а
у
х
хi
yi

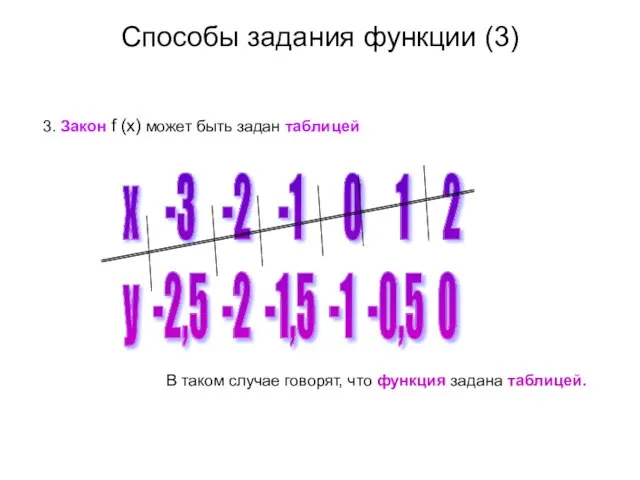
Способы задания функции (3)
3. Закон f (x) может быть задан таблицей
x -3 -2 -1 0 1 2
y -2,5 -2 -1,5 -1 -0,5 0
В таком случае говорят, что функция задана таблицей.

Область определения и область значений функции (1)
Область определения функции (ООФ) образуют все значения, которые принимает независимая переменная х.
ООФ состоит из всех значений независимой переменной х, при которых формула имеет смысл:
Функция задана формулой:
x – любое действительное число;
x ≥ - 4;
x ≠ - 4;
x є [- 0,5; 5 ) υ ( 5; ∞ );