Содержание
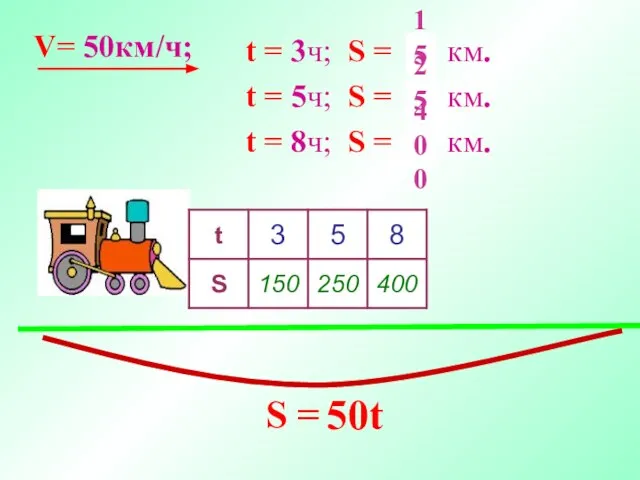
- 2. 50t V= 50км/ч; t = 3ч; S = ? км. t = 5ч; S = ?
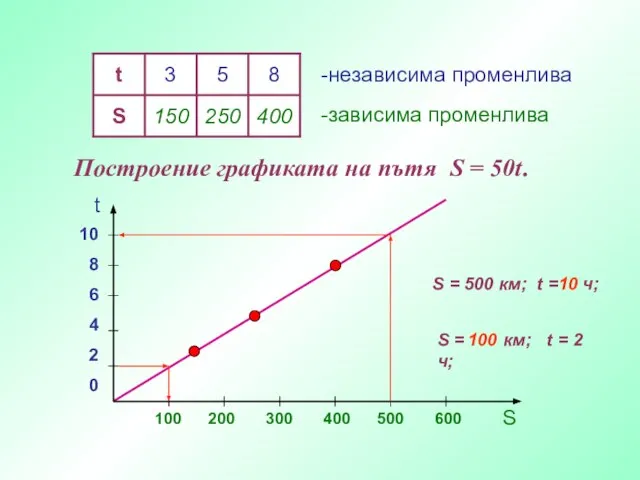
- 3. -независима променлива -зависима променлива Построение графиката на пътя S = 50t. t S 100 200 300
- 4. Определение. Казва се, че е зададена числовата функция y = f(x), когато на всяко число х
- 5. f – функция x (независима променлива) - аргумент на функцията y – стойност на функцията в
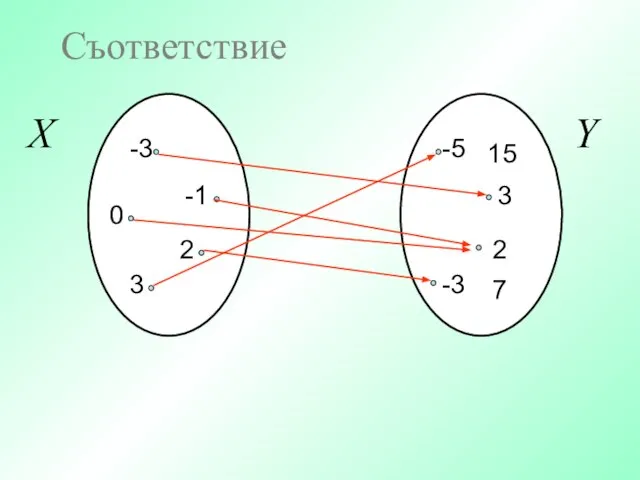
- 6. -3 -1 -5 3 2 -3 Y X Съответствие 7 15
- 7. Е дадено правилото, с помоща на което на независимата променлива x се намира (съпоставя) съответната стойност
- 8. Намерете D (f), ако
- 9. Графика Графика на функция – множеството от всички точки в равнината, абсцисите на които са равни
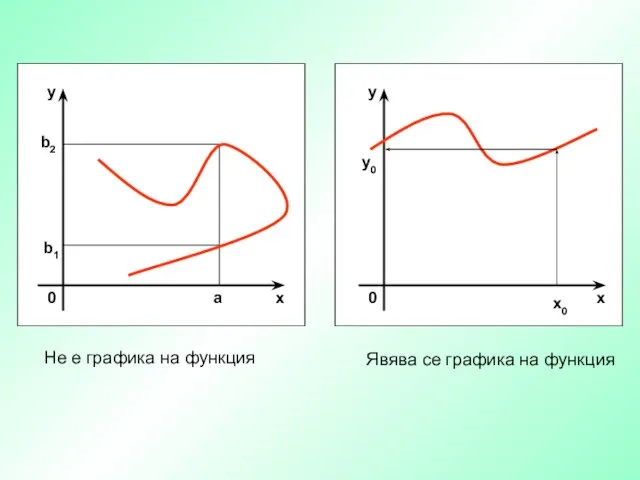
- 10. b1 b2 a x0 y0 Не е графика на функция Явява се графика на функция
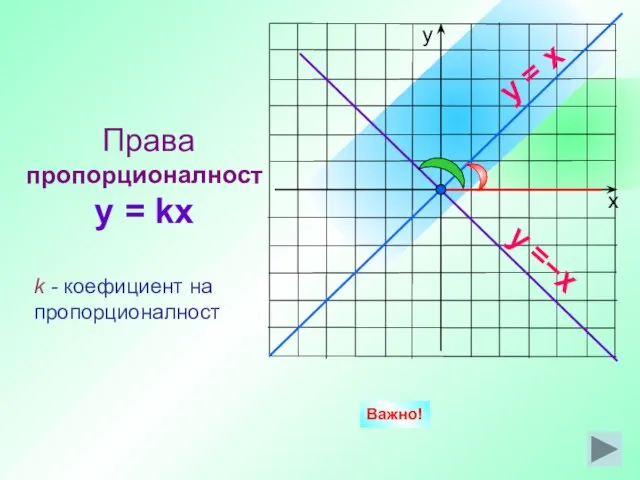
- 11. Права пропорционалност y = kx y = x y =−x Важно! k - коефициент на пропорционалност
- 12. Обратна пропорционална зависимост
- 13. Да построим графиката на функцията у =
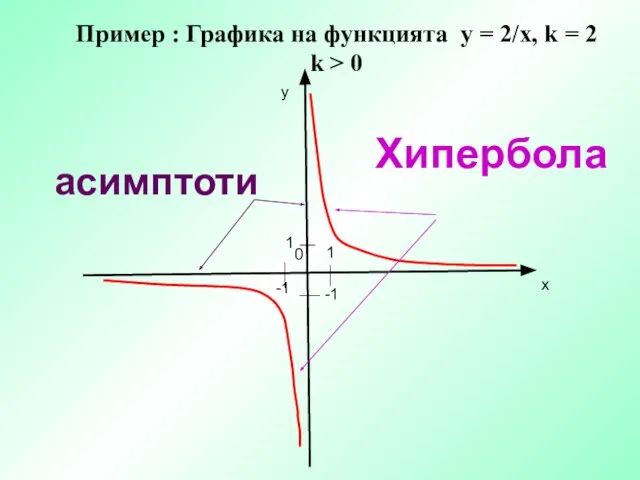
- 14. Пример : Графика на функцията у = 2/х, k = 2 k > 0 у х
- 15. Функция от вида y = kx + b, където к и в са константи се нарича
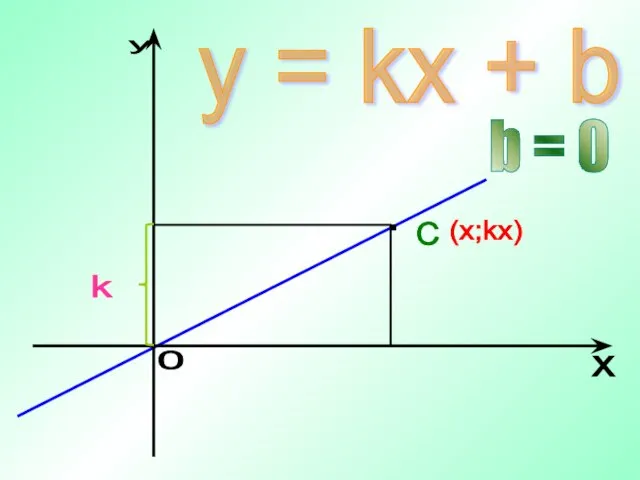
- 16. y = kx + b b = 0
- 17. y = kx + b M1 k > 0
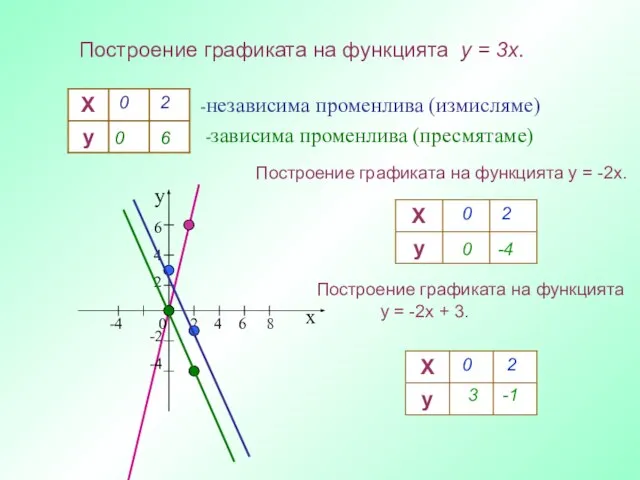
- 18. Построение графиката на функцията y = 3x. -независима променлива (измисляме) -зависима променлива (пресмятаме) 0 2 0
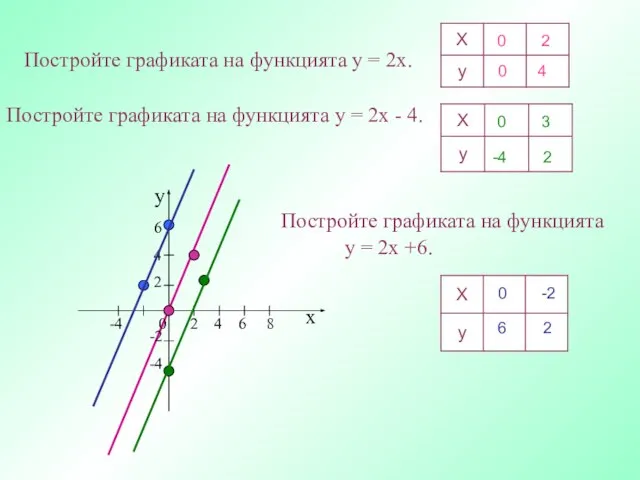
- 19. Постройте графиката на функцията y = 2x. х у -4 0 2 4 6 8 6
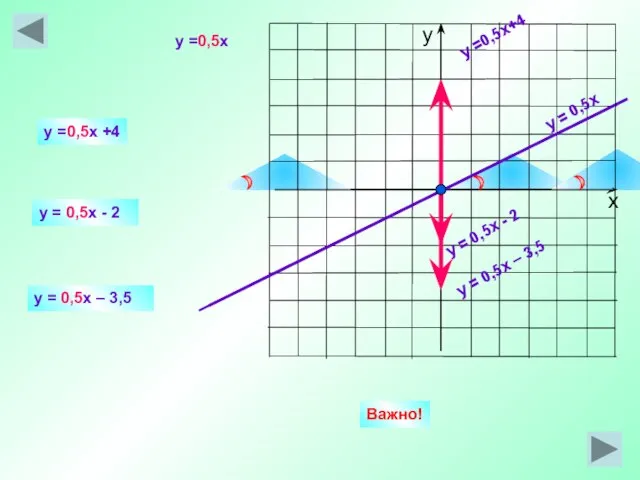
- 20. y = 0,5x y =0,5x+4 y = 0,5x - 2 y =0,5x +4 y = 0,5x
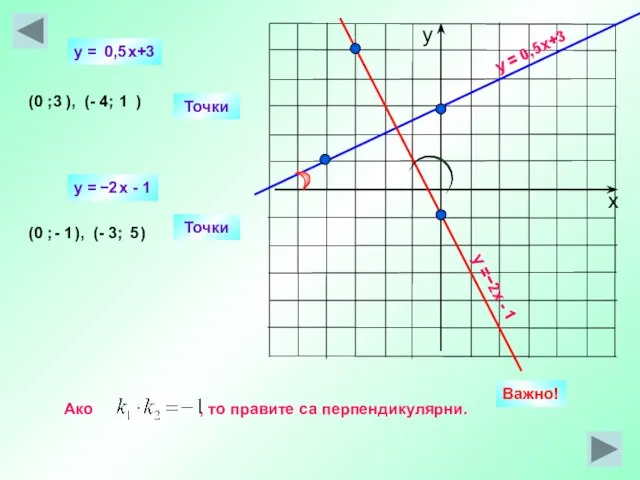
- 21. y = 0,5x+3 y =−2х - 1 Точки (0 ; ), (- 4; ) Точки (0
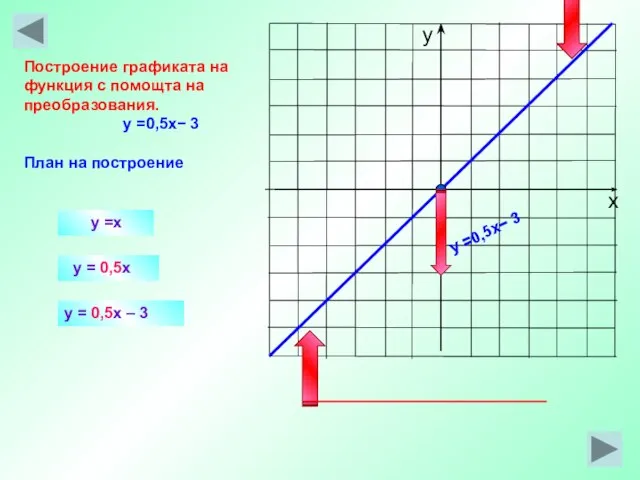
- 22. y =x y = 0,5x Построение графиката на функция с помощта на преобразования. y =0,5x− 3
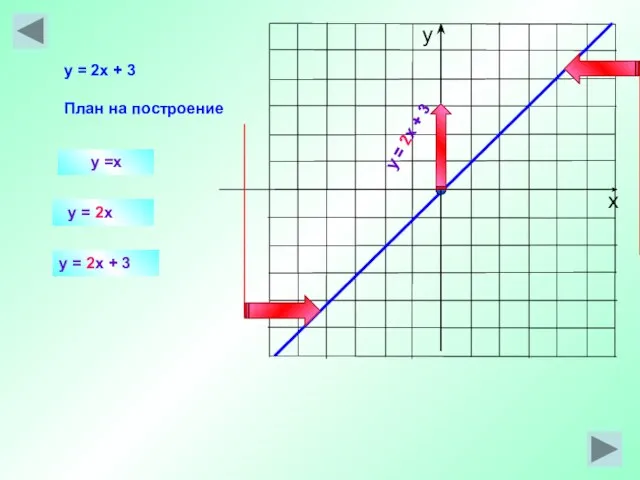
- 23. y =x y = 2x y = 2x + 3 План на построение y = 2x
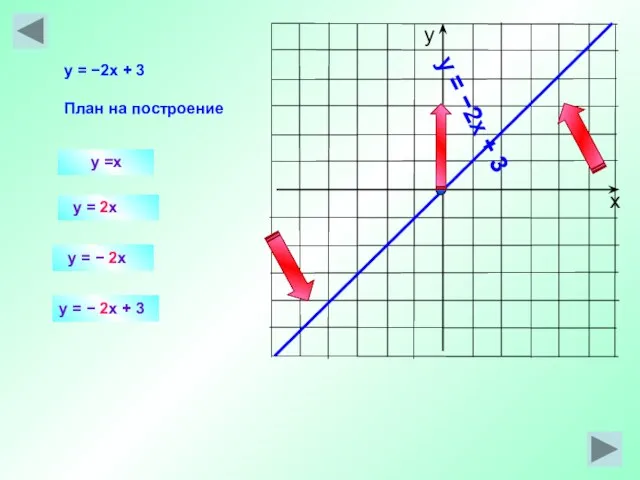
- 24. y =x y = 2x y = −2x + 3 План на построение y = −
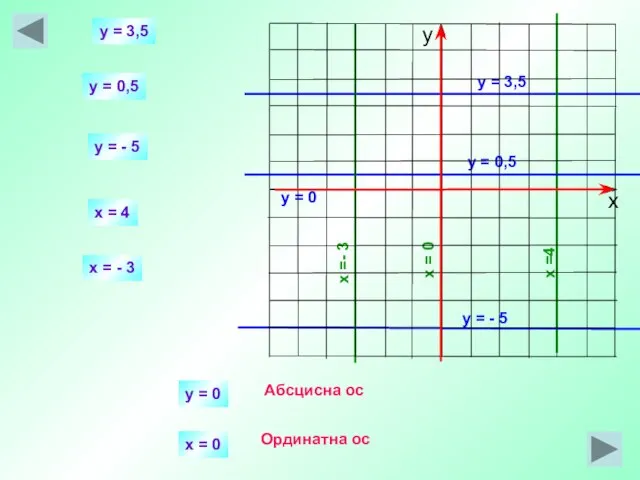
- 25. y = 3,5 x =4 y = 3,5 x = 4 y = 0,5 y =
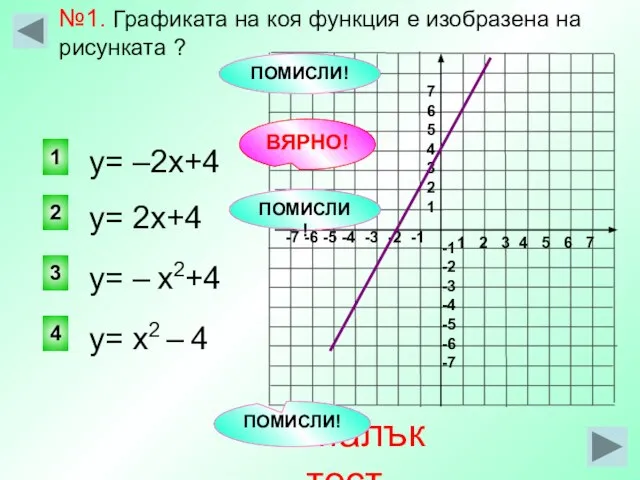
- 26. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6
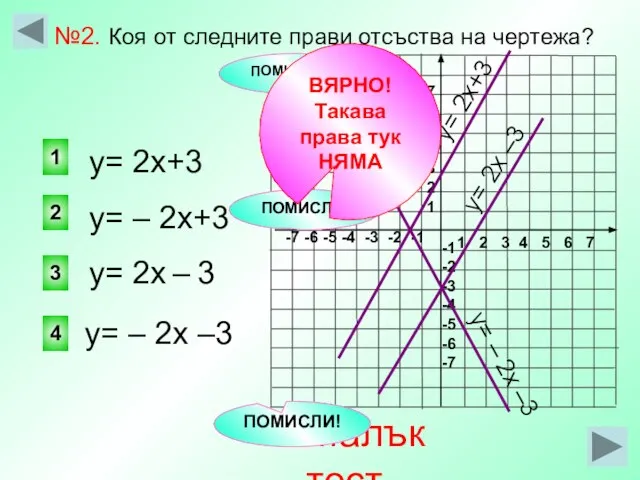
- 27. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6
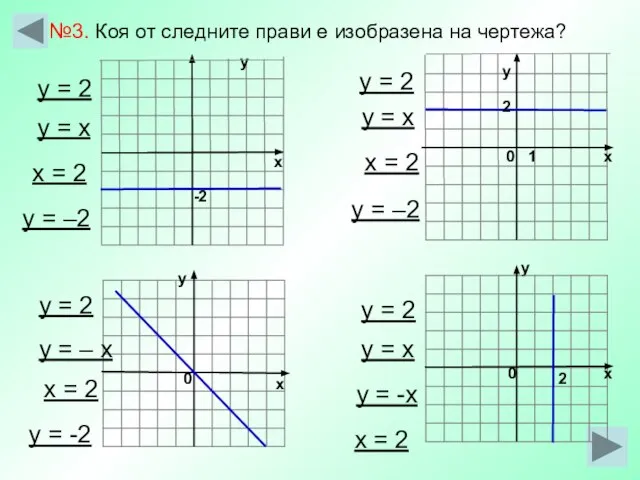
- 28. -2 х у у х у 0 1 0 2 у х №3. Коя от следните
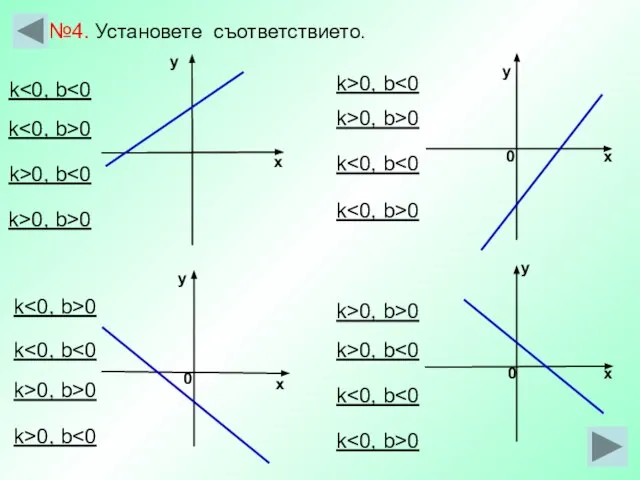
- 29. х у у х у 0 х 0 0 у х №4. Установете съответствието. k k
- 31. Скачать презентацию








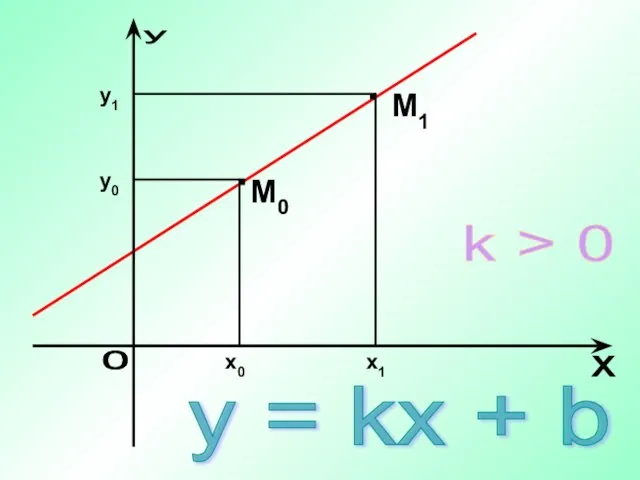
 Боевые традиции вооружённых сил России
Боевые традиции вооружённых сил России Рекомендации по подготовке доклада
Рекомендации по подготовке доклада Тайны русского слова
Тайны русского слова Лингвистический компонент обучения: спектр возможностей по обновлению содержания образования
Лингвистический компонент обучения: спектр возможностей по обновлению содержания образования Мисс Гуманитарный Институт 2020. Конкурс красоты, таланта и ума
Мисс Гуманитарный Институт 2020. Конкурс красоты, таланта и ума Основные рекомендации к разработке и проведению здоровьесберегающего урока
Основные рекомендации к разработке и проведению здоровьесберегающего урока Воспитательная программа «Любознайки»
Воспитательная программа «Любознайки» Традиции празднования Рождества в США
Традиции празднования Рождества в США pervaya_mirovaya_voyna_-_oruzhie
pervaya_mirovaya_voyna_-_oruzhie Презентация на тему Интересные факты о пресмыкающихся
Презентация на тему Интересные факты о пресмыкающихся  Зона рецепшена. Минималистичный легкий стул
Зона рецепшена. Минималистичный легкий стул Обращение в кризисный центр женщинам
Обращение в кризисный центр женщинам Агентство рекламы полного циклаРАНДАР
Агентство рекламы полного циклаРАНДАР Электромобиль - машина будущего или уже реальность
Электромобиль - машина будущего или уже реальность Третьяковская галерея (3 класс)
Третьяковская галерея (3 класс) C:\Documents and Settings\Администратор\Рабочий стол\Рисунок1.pngВелика Россия, а отступать некуда: позади- Москва!
C:\Documents and Settings\Администратор\Рабочий стол\Рисунок1.pngВелика Россия, а отступать некуда: позади- Москва! Система управления ключевыми показателями эффективности в энергосбытовых компаниях
Система управления ключевыми показателями эффективности в энергосбытовых компаниях Природа. Фото
Природа. Фото Смена по предпринимательству
Смена по предпринимательству Порушка-Пораня
Порушка-Пораня Объемы тел
Объемы тел Латвийская Советская Социалистическая Республика
Латвийская Советская Социалистическая Республика Творческий проект Декоративное панно «Весна-красна на землю пришла» Кружевоплетение
Творческий проект Декоративное панно «Весна-красна на землю пришла» Кружевоплетение Рекорды планеты
Рекорды планеты Образ лирической героини в поэтическом цикле А. Блока «Кармен»
Образ лирической героини в поэтическом цикле А. Блока «Кармен» Этот многоликий стресс
Этот многоликий стресс Bientôt les vacances, venez visiter Paris
Bientôt les vacances, venez visiter Paris Музей воды в Киеве
Музей воды в Киеве