Геометрия.

Тема: параллелограмм.

Определение:
Определение: параллелограмм - четырехугольник,
у которого противоположные стороны попарно параллельны.

Свойства параллелограмма:

Свойства параллелограмма:
Диагонали параллелограмма пересекаются и точкой пресечения делятся пополам.
Параллелограмм – выпуклый четырехугольник.
У параллелограмма противолежащие стороны равны, противолежащие углы равны.

Признаки параллелограмма:
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
Если у четырехугольника противолежащие стороны попарно равны, такой четырехугольник – параллелограмм.
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.

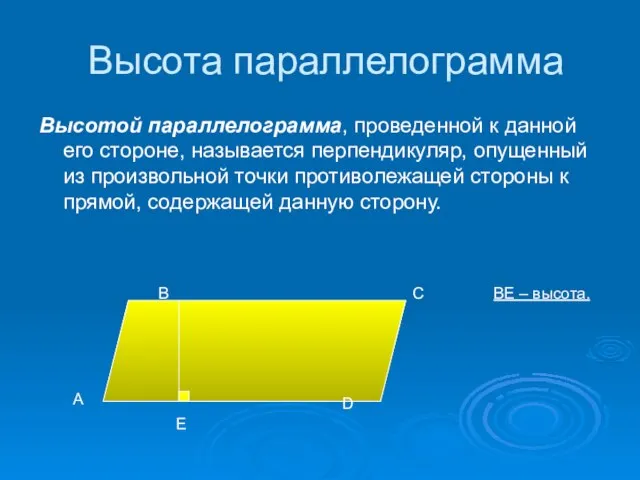
Высота параллелограмма
Высотой параллелограмма, проведенной к данной его стороне, называется перпендикуляр, опущенный из произвольной точки противолежащей стороны к прямой, содержащей данную сторону.
BE – высота.

Площадь параллелограмма:
Площадь параллелограмма равна произведению его стороны на проведенную к ней высоту: S = ah.
a
h

Задачи.
Часть «A».

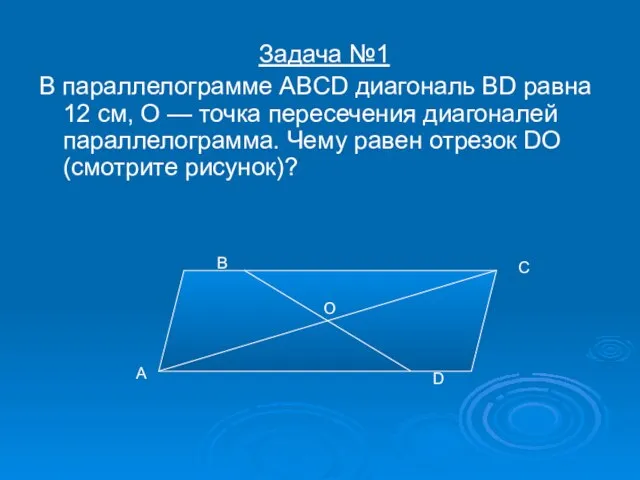
Задача №1
В параллелограмме ABCD диагональ BD равна 12 см, О — точка пересечения диагоналей параллелограмма. Чему равен отрезок DO (смотрите рисунок)?

Решение:
Диагональ BD в параллелограмме ABCD точкой O делится пополам (свойство параллелограмма). Значит BO=OD=6 .
Ответ: DO=6.
Задача №2.
В параллелограмме сумма двух углов равна 132°. Найдите градусную меру каждого из этих углов.

Решение:
Эти углы не могут быть прилежащими к одной стороне, так как в этом случае бы их сумма была бы равна 180°: Значит, эти углы противолежащие. По свойству противолежащих углов параллелограмма они равны и каждый из них равен 66°.
Ответ: 66°.
Задача №3
Стороны параллелограмма 4 см и 6 см. Меньшая его высота равна 3 см. Вычислите второю высоту параллелограмма.

Решение:
Площадь параллелограмма равна
и . Так как S=aha= ah b , то меньшая высота соответствует большей стороне, значит
меньшая высота опущена на сторону длиной 6 см. Значит S=18 см2 , а искомая высота равна
и равна 4,5 см.

Задача№4
Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Решение:
Пусть ABCD - данный параллелограмм,
AK - указанная биссектриса, BK=7 , KC=14.
Поскольку углы BKA, KAD, BAK равны ,
то треугольник ABK - равно-
бедренный. Поэтому AB=BK=7,
BC=BK+KC=21. Значит периметр равен 56.

Часть " B " !

Задача № 1
Даны две окружности с общим центром в точке О, АС и BD — диаметры этих окружностей. Докажите, что четырехугольник ABCD — параллелограмм.

Решение:
Доказательство. Так как О — центр концентрических окружностей, то диаметры АС и CD пересекаются и точкой пересечения делятся пополам, значит, ABCD — параллелограмм.

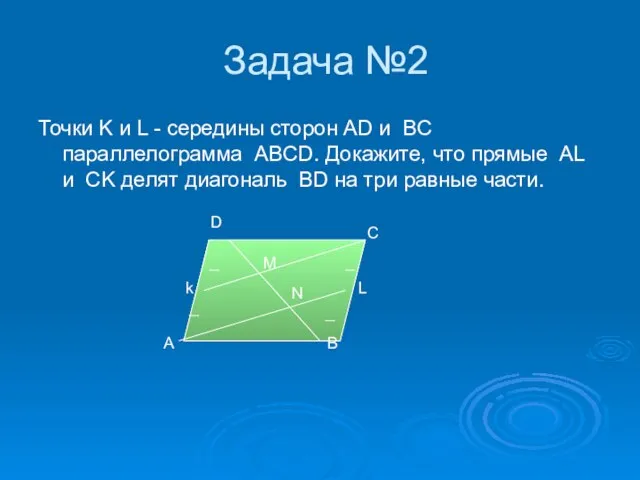
Задача №2
Точки K и L - середины сторон AD и BC параллелограмма ABCD. Докажите, что прямые AL и CK делят диагональ BD на три равные части.
A
B
C
D
k
L
N
M

Решение:
KD = AK, CL = BL. Так как ABCD - параллелограмм, то AD || BC, следовательно, AK || CL, причем AK = CL, так как AD = BC. Тогда по признаку параллелограмма имеем, что ALCK - параллелограмм. Следовательно, KM || AN и NL|| CM. Причем KM проходит через середину AD , а NL - через середину BC. Значит, KM - средняя линяя тр. ADN, а NL - cредняя линяя тр. BCM. Значит, DM = MN и BN = MN или DM = MN = BN.

Часть " C " !

Задача №1
Дан параллелограмм ABCD с острым углом при вершине A . На лучах AB и CB отмечены точки H и K соответственно так, что CH=BC и AK=AB .
а) Докажите, что DH=DK .
б) Докажите, что треугольники DKH и ABK подобны.

Решение:
Из равенства треугольников HCD и DAK (по двум сторонам и углу между ними) следует равенство отрезков DH и DK .
Из равенства углов KAH и HCK следует, что точки A,C,H,K - лежат на одной окружности, а так как угол CKA и угол ADC в сумме 180 градусов , то на этой окружности лежит и точка D .
Следовательно, углы KAB и KDH при вершинах A и D равнобедренных треугольников ABK и DKH равны. Поэтому треугольники подобны.

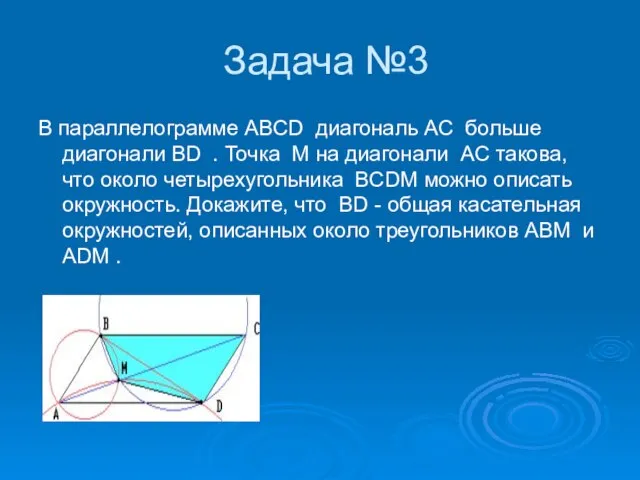
Задача №3
В параллелограмме ABCD диагональ AC больше диагонали BD . Точка M на диагонали AC такова, что около четырехугольника BCDM можно описать окружность. Докажите, что BD - общая касательная окружностей, описанных около треугольников ABM и ADM .

Решение:
Поскольку углы MBD, MCD, BAM равны, а точки A и D лежат по разные стороны от прямой BM , то BD - касательная к окружности, описанной около треугольника ABM .
Задача № 4
В параллелограмме ABCD с углом A , равным 60 градусов , проведена биссектриса угла B , пересекающая сторону CD в точке E . В треугольник ECB вписана окружность радиуса R . Другая окружность вписана в трапецию ABED . Найдите расстояние между центрами этих окружностей.

Решение:
Пусть O1 и O2 - центры окружностей, вписанных в треугольник BCE и в ABED трапецию .
Треугольник O1EO2 - прямоугольный, т. к. угол O1EO2 - прямой (угол между биссектрисами смежных углов).
Треугольник BCE - равносторонний (углы BEC, ABE, EBC равны между собой и равны 60 градусов ), O1E=2R , его высота EM равна 3R . Поэтому O2B=EM=3R . Тогда
Следовательно,
Ответ:

Задача №5
В параллелограмме лежат две окружности, касающиеся друг друга и трех сторон параллелограмма каждая. Радиус одной из окружностей равен 1. Известно, что один из отрезков стороны параллелограмма от вершины до точки касания равен . Найдите площадь параллелограмма.

Решение:
Окружности равны. Расстояние между точками их касания с большей стороной параллелограмма равно сумме их радиусов, т. е. 2. Меньшая сторона параллелограмма видна из центра касающейся ее окружности под прямым углом. Один из отрезков этой стороны от вершины до точки касания равен , значит второй равен . Тогда большая сторона равна
Следовательно, площадь параллелограмма равна 2(
).

Задача №6:
В параллелограмме ABCD острый угол равен . Окружность радиуса r проходит через вершины A,B,C и пересекает прямые AD и CD в точках M и N . Найдите площадь треугольника BMN .

Решение: