Слайд 2Статистика.
Статистика –наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных

массовых явлениях, происходящих в природе и обществе. Слово « статистика» происходит от латинского слова status, которое означает « состояние, положение вещей»
Статистика знает всё!
Известно, сколько, какой пищи съедает в год в среднем гражданин республики. Сколько в стране охотников, балерин, артистов, рабочих и т. д.
Результаты статистических исследований широко используются для практических и научных выводов. Статистические характеристики применяют для нахождения средней урожайности пшеницы с 1 га в данном районе, среднего суточного удоя молока от одной коровы на ферме и
т.п.
Слайд 3Демографическая статистика.
В демографии большую роль играет
демографическая статистика, изучающая численность населения,

социальный, профессиональный состав, передвижение населения в пределах страны.
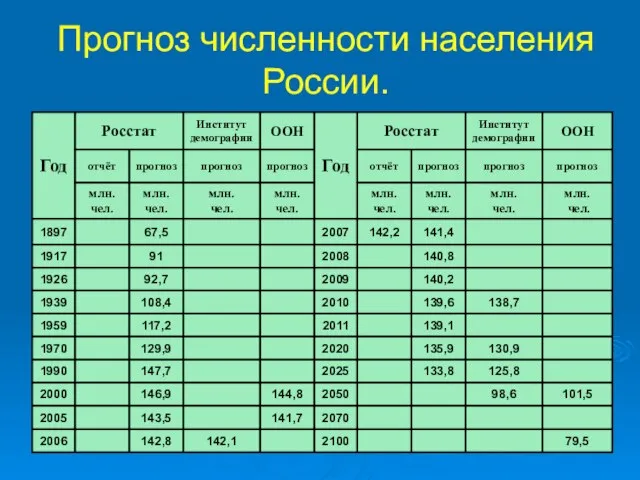
Слайд 4Прогноз численности населения России.
Слайд 5Экономическая статистика.
Экономическая статистика разрабатывает методы прогнозирования роста или спада производственной продукции,

изменение цен, спроса и предложения на товары.
Слайд 6Методы обработки статистических данных во всех известных видах статистики имеют много общего

и основаны на знании теории вероятностей.
Слайд 7Вероятность.
Встречаясь в жизни с различными событиями, мы часто даём оценку степени их

достоверности.
«Это невероятно!» - говорим о невозможном событии, например о том, что вода в холодильнике закипела.
«Маловероятно, что сегодня будет дождь»,- говорим, глядя на безоблачное небо летним утром.
«Шансы равны», «шансы 50/50» - говорим, например, о возможности победы в соревнованиях двух спортсменов или когда делаем ставку на орла или решку при подбрасывании монеты.
Долю успеха того или иного события в математике стали называть вероятностью этого события и обозначать буквой Р (по первой букве латинского слова probabilitas – вероятность).
Слайд 8Справедливые и несправедливые игры.
Равными вероятностями появления орла и решки при бросании монеты

часто пользуются для принятия решения в спорных ситуациях «например, при розыгрыше ворот в футболе».
Игра в рулетку – несправедливая игра. Игрок в рулетку поставивший 1 жетон например, на линию, выигрывает 5 жетонов с вероятностью 6/37 и проигрывает 1 жетон с вероятностью 31/37. Поэтому математическое ожидание его выигрыша равно – 1/37, игра явно небезобидная и выгодна игорному дому, который с каждого поставленного жетона имеет 1/37 жетона.
Слайд 9Задача.
В одной комнате общежития живут Антон, Борис и Василий. Нужно регулярно назначать

дежурного по комнате. Юноши подбрасывают две монеты и в зависимости от результата определяют дежурного:
- если выпали орёл и решка, дежурит Антон,
- если выпали два орла, дежурит Борис,
- если выпали две решки, дежурит Василий.
Справедлив ли такой подход к выбору дежурного?
Слайд 10Решение.
Такой подход не является справедливым, так как вероятность появления орла и решки

( ОР или РО ) равна 1/2 ( два благоприятствующих из четырёх возможных исходов), а вероятности появления двух решек или двух орлов одинаковы и равны 1/4. Так как ½ / ¼ = 2 , то можно сказать, что Антону, по всей вероятности, придётся в 2 раза чаще дежурить, чем каждому из его друзей.
Слайд 11Элементы логики, комбинаторики, статистики и теории вероятностей.
(45 часов)
Доказательство. Определения, доказательства, аксиомы и

теоремы; следствия. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы.
Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат Евклида и его история.
Множества и комбинаторика. Множество. Элемент множества , подмножество. Объединение и пересечение множеств. Диаграммы Эйлера.
Примеры решений комбинаторных задач. Перебор вариантов, правило умножения.
Статистические данные. Представление данных в виде таблиц, графиков, диаграмм. Средние результаты измерений. Понятие о статистическом выводе на основе выборки.
Понятие и примеры случайных событий.
Вероятность. Частота события. Вероятность. Равновозможные события и подсчёт их вероятности. Представление о геометрической вероятности.
Слайд 12Элементы логики, комбинаторики, статистики и теории вероятностей.
Уметь
проводить несложные доказательства, получать простейшие следствия

из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений. Использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы, графики;
решать комбинаторные задачи путём систематического перебора возможных вариантов с использованием правила умножения,
вычислять средние значения результатов измерений,
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
Слайд 13Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
выстраивания

аргументации при доказательстве и диалоге;
распознавания логически некорректных рассуждений;
записи математических рассуждений, доказательств,
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объёмов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
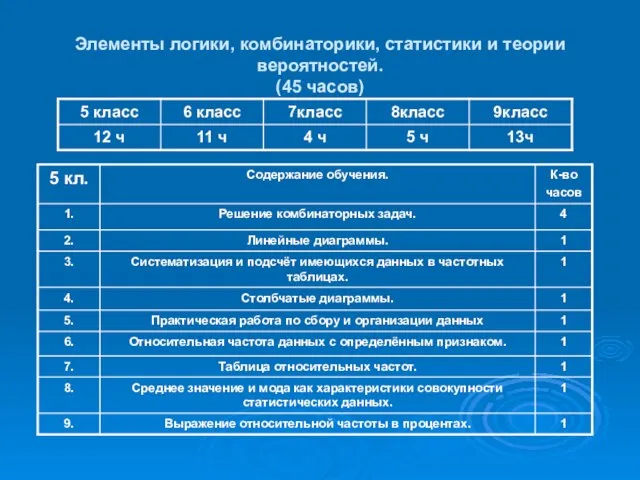
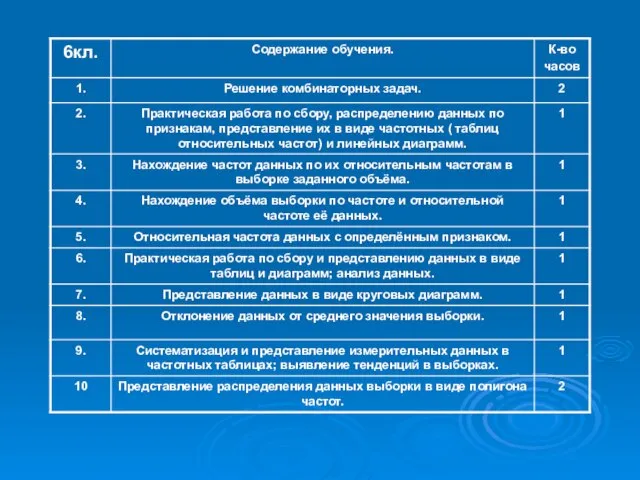
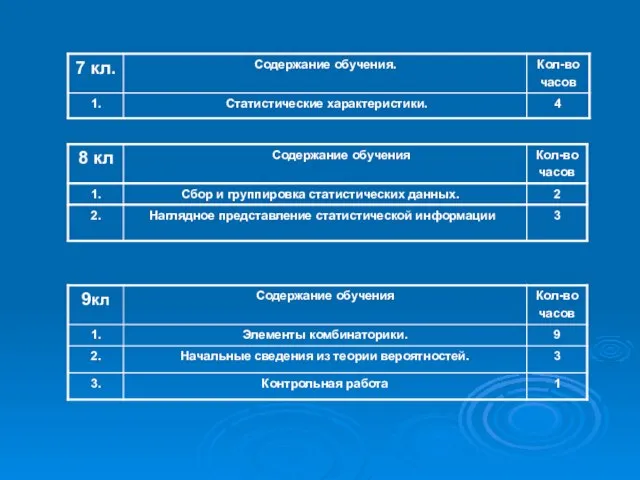
Слайд 14Элементы логики, комбинаторики, статистики и теории вероятностей.
(45 часов)
Слайд 17Литература.
Программы общеобразовательных учреждений. Алгебра 7-9 кл.
Составитель: Т.А. Бурмистрова. Москва «Просвещение» 2008

г.
Элементы статистики и теории вероятностей. Ю.Н.Макарычев Москва «Просвещение» 2006 г.
Энциклопедия для детей. Математика.
Редколлегия М. Аксёнова, В. Володин. Москва 2005г.
Математическая учительская: http://www.math.ru
Сеть творческих учителей: http://.it-n.ru
http://www.kaverkon.ru














 ES-5844P
ES-5844P Жизнь диких животных зимой
Жизнь диких животных зимой Лекция 3 Безопасная эксплуатация сосудов, работающих под давлением Цель занятия: Изучить основные правила безопасности при эксплу
Лекция 3 Безопасная эксплуатация сосудов, работающих под давлением Цель занятия: Изучить основные правила безопасности при эксплу Этико-эстетическая культура управления в органах внутренних дел. Культура руководителей внутренних дел
Этико-эстетическая культура управления в органах внутренних дел. Культура руководителей внутренних дел Презентация проектаИинтегрированное Управление Персоналом- Федеральная земля Берлин -Референц-визит от 20.10.2005в Берлине
Презентация проектаИинтегрированное Управление Персоналом- Федеральная земля Берлин -Референц-визит от 20.10.2005в Берлине Проект «создание макета экогруппы моря мезозойской эры»
Проект «создание макета экогруппы моря мезозойской эры» Анод + Катод = Электролиз
Анод + Катод = Электролиз Pirates of the Caribbean
Pirates of the Caribbean УРОК ПРАВА В 1-4 КЛАССАХ
УРОК ПРАВА В 1-4 КЛАССАХ  Смысловая цельность, речевая связность и последовательность изложения
Смысловая цельность, речевая связность и последовательность изложения Планируемые результаты начального общего образования
Планируемые результаты начального общего образования Взаимоотношения с Западом
Взаимоотношения с Западом Разложение электромагнитного поля резонатора по пространственно локализованным базисным функциям
Разложение электромагнитного поля резонатора по пространственно локализованным базисным функциям Выпускники ТМИ 1966 года. 30 лет спустя
Выпускники ТМИ 1966 года. 30 лет спустя 20140111_chudesa_sveta
20140111_chudesa_sveta Разработка нормативно-методическихдокументов, регламентирующихинформационный обмен в книжном деле(издатель-книготорговец-пок
Разработка нормативно-методическихдокументов, регламентирующихинформационный обмен в книжном деле(издатель-книготорговец-пок Формирование информационной основы для проведения сплошного наблюдения субъектов малого и среднего предпринимательства
Формирование информационной основы для проведения сплошного наблюдения субъектов малого и среднего предпринимательства Современные средства поражения и их поражающие факторы
Современные средства поражения и их поражающие факторы По дорогам права. Онлайн-викторина
По дорогам права. Онлайн-викторина Управленческая мысль в эпоху Европейского средневековья
Управленческая мысль в эпоху Европейского средневековья Team_7
Team_7 Технология лесозаготовок. Клён остролистый
Технология лесозаготовок. Клён остролистый Планирование собственного развития. Персональный предпринимательский проект
Планирование собственного развития. Персональный предпринимательский проект ИЗОЛЯЦИЯ И ПЕРЕНАПРЯЖЕНИЯ
ИЗОЛЯЦИЯ И ПЕРЕНАПРЯЖЕНИЯ Презентация на тему Один день из жизни Обломова «Один день – и вся жизнь» Н.А.Добролюбов
Презентация на тему Один день из жизни Обломова «Один день – и вся жизнь» Н.А.Добролюбов  Символизм в искусстве
Символизм в искусстве Презентация на тему Обучение учащихся с разной функциональной асимметрией полушарий
Презентация на тему Обучение учащихся с разной функциональной асимметрией полушарий Школа дошкольника «Первые шаги»2 год обучения
Школа дошкольника «Первые шаги»2 год обучения