Слайд 2Понятие информация
является одним из самых фундаментальных понятий в современной науке вообще

и базовым понятием для информатики.
Информация - третья сущность мира (наряду с веществом и энергией)
Неопределяемое понятие, (как в математике "точка" или "прямая«)
Слайд 3Различные определения информации
Сведения о каких-либо, ранее неизвестных объектах, явлениях или событиях;
Содержательное описание

объекта или явления;
Содержание сигнала, сообщения;
Мера разнообразия;
Отраженное разнообразие;
Уменьшение неопределенности;
Уменьшение энтропии;
Продукт научного познания;
Содержание отображения реальной действительности;
Третья сущность мира (наряду с материей и энергией);
Свойство материи.
Слайд 4"информация" - некоторые сведения, данные, знания и т.п
Информация передается в виде сообщений,

определяющих форму и представление передаваемой информации
При этом предполагается, что имеются "источник информации" и "получатель информации". Сообщение от источника к получателю передается посредством какой-либо среды, являющейся в таком случае "каналом связи"
Слайд 5Различные уровни представлений об информации
Человеку свойственно субъективное восприятие информации через некоторый

набор ее свойств:
важность,
достоверность,
своевременность,
доступность.
при объективном измерении количества информации следует заведомо отрешиться от восприятия ее с точки зрения субъективных свойств
Слайд 6Непрерывная и дискретная информация
Чтобы сообщение было передано от источника к получателю,

необходима некоторая материальная субстанция - носитель информации.
Сообщение, передаваемое с помощью носителя, назовем сигналом.
В общем случае сигнал - это изменяющийся во времени физический процесс. Такой процесс может содержать различные характеристики (например, при передаче электрических сигналов может изменяться напряжение и сила тока).
Та из характеристик, которая используется для представления сообщений, называется параметром сигнала
Слайд 7Непрерывная и дискретная информация
В случае, когда параметр сигнала принимает последовательное во

времени конечное число значений (при этом все они могут быть пронумерованы) сигнал называется дискретным, а сообщение, передаваемое с помощью таких сигналов - дискретным сообщением.
Информация, передаваемая источником в этом случае, также называется дискретной.
Если же источник вырабатывает непрерывное сообщение (соответственно параметр сигнала - непрерывная функция от времени), то соответствующая информация называется непрерывной.
Слайд 8измерение количества информации
вероятностный (или кибернетический) подход к измерению количества информации( 40-е

годы XX века американский математик Клод Шеннон)
объемному подходу в измерении информации (создание вычислительной техники)
Слайд 9вероятностный подход
Бросание игральной кости, имеющей N граней(N=6)
Энтропия (Н) - численная величина,

измеряющая неопределенность
H = f(N),
1.Готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность. Обозначим ее H1.
2. Кость брошена; информацию об исходе данного опыта получена. Обозначим количество этой информации через I.
3. Обозначим неопределенность данного опыта после его осуществления через H2.
За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей, имевшихся "до" и "после" опыта:
I = H1 - H2
Слайд 10формула Хартли.
М - количество бросаний кости
Х - общее число исходов, X=NM
в

случае двух бросаний кости с шестью гранями имеем: X=62=36
бросание M раз кости можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем - "однократных бросаний кости". Энтропия такой системы в M раз больше, чем энтропия одной подсистемы f(6M)=Mf(6)
Данную формулу можно распространить и на случай любого N: f(NM)=Mf(N)
Слайд 11формула Хартли.
Прологарифмируем левую и правую часть формулы X=NM : ln X =

M* ln N, M = ln X / ln N
Подставляем полученное для M значение в формулу f(NM)=Mf(N) : f(X) =(ln X/ ln N)* f(N)
Обозначив константу K = f(N)/ln(M) ,получим:
f(X) = K * ln X
или, с учетом H = f(N), H = K * ln N
Обычно принимают K =1/ln2 и, таким образом
H=log2 N
эта формула называется формула Хартли.
Слайд 12Единица измерения информации
Важным при введение какой либо величины является вопрос о том,

что принимать за единицу ее измерения.
Очевидно, H будет равным 1 при N = 2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты при котором возможны два исхода: "орел", "решка").
Такая единица количества информации называется "бит".
Слайд 13формула Шеннона.
Все N исходов рассмотренного выше опыта являются равновероятными и поэтому можно

считать, что на "долю" каждого исхода приходится одна N-я часть общей неопределенности опыта: ( log2 N) / N
При этом вероятность i-го исхода Pi равняется, очевидно,1/N.
Таким образом:
Та же формула принимается за меру энтропии в случае, когда вероятности различных исходов опыта неравновероятны (т.е. Pi могут быть различны).
Эта формула называется формулой Шеннона.
Слайд 14Пример
определить количество информации, связанное с появлением каждого символа в сообщениях, записанных на

русском языке.
Будем считать, что русский алфавит состоит из 33 букв и знака "пробел" для разделения слов. Т.е. мощность нашего алфавита = 34 По формуле Хартли имеем:
H=log234 ≈ 5 бит.
Слайд 15Пример
Однако, в словах русского языка (равно как и в словах других языков)

различные буквы встречаются неодинаково часто. Построена таблица вероятностей всех знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.
Воспользуемся для подсчета H формулой Шеннона:
H ≈ 4.72 бит.
Полученное значение для H, как и можно было предположить, меньше вычисленного ранее. Эта величина является максимальным количеством информации, которое могло бы приходиться на один знак
Слайд 16Пример
Рассмотрим алфавит, состоящий из двух знаков "0" и "1". (Мощность алфавита =

2) Если считать, что со знаками "0" и "1" в двоичном алфавите связаны одинаковые вероятности их появления (а конкретно: P("0")= P("1")= 0.5), то количество информации на один знак при двоичном кодировании будет равно
H = log22= 1 бит.
Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
Слайд 17 Объемный подход
При работе в принятой для представления информации в компьютере двоичной

системе счисления знаки "0" и "1" будем называть битами (от английского выражения BInary digiTs - двоичные цифры).
С точки зрения аппаратной организации компьютера бит, очевидно, является наименьшей возможной единицей информации. Объем же информации в некотором тексте, записанном двоичными знаками подсчитывается просто по количеству двоичных символов.
При этом, в частности, невозможно нецелое количество битов (в отличие от кибернетического подхода).
Слайд 18Для удобства использования введены более крупные чем бит единицы количества информации.
Байт

- Двоичное слово из восьми знаков (и количество информации, содержащейся в нем).
килобайт (Кбайт) - 1024 байта,
мегабайт (Мбайт) - 1024 килобайта
гигабайт (Гбайт) - 1024 мегабайта
Слайд 19соотношение между вероятностным и объемным количеством информации
энтропийное количество информации не может быть

больше числа двоичных битов в сообщении, только меньше или равно.
Если энтропийное количество информации меньше объемного, то говорят, что сообщение избыточно.
Примером избыточных сообщений могут служить очевидные, тривиальные сообщения типа «Каждый день встает солнце» «Волга впадает в Каспийское море», которые всегда избыточны, так как содержат нулевую информацию с точки зрения уменьшения энтропии, но содержат ненулевой количество символов.
Слайд 20Измерение информации в широком смысле
При анализе информации социального (в широким смысле) происхождения

на первый план могут выступить такие ее свойства как
истинность,
своевременность,
ценность,
полнота.
Их невозможно оценить в терминах "уменьшение неопределенности" (вероятностный подход) или количества символов (объемный подход).
Слайд 21Физическая трактовка информации
Информацию в физическом смысле следует считать особым видом ресурса

– неистощаемым ресурсом
набор основных с точки зрения физической интерпретации свойств информации:
запоминаемость;
передаваемость;
преобразуемость;
воспроизводимость;
стираемость
Слайд 22 Информация как философская категория
Понятие информации нельзя считать лишь техническим, междисциплинарным

и даже наддисциплинарным термином. Информация это фундаментальная философская категория
Информация есть содержание образа, формируемого в процессе отражения
Слайд 23Социальная значимость информации
в социальной действительности информация достаточно часто становятся товаром (информационный обмен)
информационная

оснащенность - одна из важнейших черт функционирования современного общества






















 Контроллер «АКД-СК»
Контроллер «АКД-СК» III Красноярский экономический форум «Развитие востока страны»Круглый «Региональная политика России и региональные стратегии к
III Красноярский экономический форум «Развитие востока страны»Круглый «Региональная политика России и региональные стратегии к Государственный санитарно-эпидемиологический надзор в области гигиены питания
Государственный санитарно-эпидемиологический надзор в области гигиены питания Модель проектно-ориентированной системы управления
Модель проектно-ориентированной системы управления Совершенствование правового положения государственных и муниципальных учреждений: организационные, финансовые, правовые аспект
Совершенствование правового положения государственных и муниципальных учреждений: организационные, финансовые, правовые аспект Курская антоновка – символ Курской области
Курская антоновка – символ Курской области Памятка о ложных вызовах об актах терроризма
Памятка о ложных вызовах об актах терроризма Изделия из слоеного теста
Изделия из слоеного теста Презентация на тему Верблюд
Презентация на тему Верблюд  Мой народ – американцы
Мой народ – американцы Презентация на тему Сергей Есенин Юность
Презентация на тему Сергей Есенин Юность  Информационные технологии в жилищно-коммунальном хозяйстве Финляндии
Информационные технологии в жилищно-коммунальном хозяйстве Финляндии Презентация на тему готовимся к ГИА, В3, В6
Презентация на тему готовимся к ГИА, В3, В6  Жанр портрета в культуре разных времён
Жанр портрета в культуре разных времён История аниме
История аниме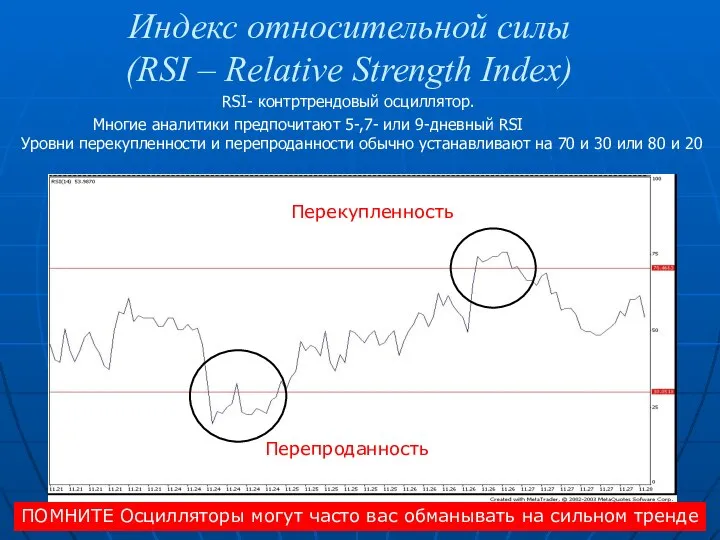 Индекс относительной силы
Индекс относительной силы Неживая и живая природа
Неживая и живая природа Реакторы, охлаждаемые водой сверхкритического давления при двухходовой схеме движения теплоносителя Ю.Д. Баранаев, А.П. Глебов, А.В
Реакторы, охлаждаемые водой сверхкритического давления при двухходовой схеме движения теплоносителя Ю.Д. Баранаев, А.П. Глебов, А.В speaking_club_yesno (2)
speaking_club_yesno (2) Мастер-класс Скрап-страницы моего лета
Мастер-класс Скрап-страницы моего лета Айларов Сослан Русланович
Айларов Сослан Русланович Елочные шарики из бумаги в технике квиллинг
Елочные шарики из бумаги в технике квиллинг Инновационная система и политика в РФ
Инновационная система и политика в РФ Семейный бюджет. Доходная и расходная части бюджета.
Семейный бюджет. Доходная и расходная части бюджета. Бухгалтерский учет, анализ и аудит
Бухгалтерский учет, анализ и аудит Праздник 1 мая
Праздник 1 мая мониторинг цен
мониторинг цен Анализ рынка детского питания на территории города Казани в одной из ключевых национальных сетей Пятерочка
Анализ рынка детского питания на территории города Казани в одной из ключевых национальных сетей Пятерочка