Слайд 2Summary
Heuristics and Optimal search strategies
heuristics
hill-climbing algorithms
Best-First search
A*: optimal search using heuristics
Properties of

A*
admissibility,
monotonicity,
accuracy and dominance
efficiency of A*
Branch and Bound
Iterative deepening A*
Automatic generation of heuristics
Слайд 3Problem: finding a Minimum Cost Path
Previously we wanted an arbitrary path to

a goal or best cost.
Now, we want the minimum cost path to a goal G
Cost of a path = sum of individual transitions along path
Examples of path-cost:
Navigation
path-cost = distance to node in miles
minimum => minimum time, least fuel
VLSI Design
path-cost = length of wires between chips
minimum => least clock/signal delay
8-Puzzle
path-cost = number of pieces moved
minimum => least time to solve the puzzle
Слайд 4Best-first search
Idea: use an evaluation function f(n) for each node
estimate of "desirability"
Expand

most desirable unexpanded node
Implementation:
Order the nodes in fringe in decreasing order of desirability
Special cases:
greedy best-first search
A* search
Слайд 5Heuristic functions
8-puzzle
8-queen
Travelling salesperson

Слайд 6Heuristic functions
8-puzzle
W(n): number of misplaced tiles
Manhatten distance
Gaschnig’s
8-queen
Travelling salesperson

Слайд 7Heuristic functions
8-puzzle
W(n): number of misplaced tiles
Manhatten distance
Gaschnig’s
8-queen
Number of future feasible slots
Min number

of feasible slots in a row
Travelling salesperson
Minimum spanning tree
Minimum assignment problem
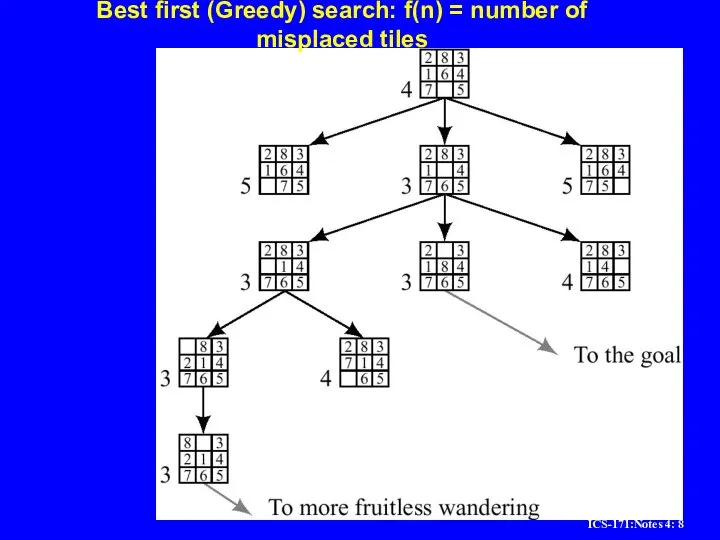
Слайд 8Best first (Greedy) search: f(n) = number of misplaced tiles
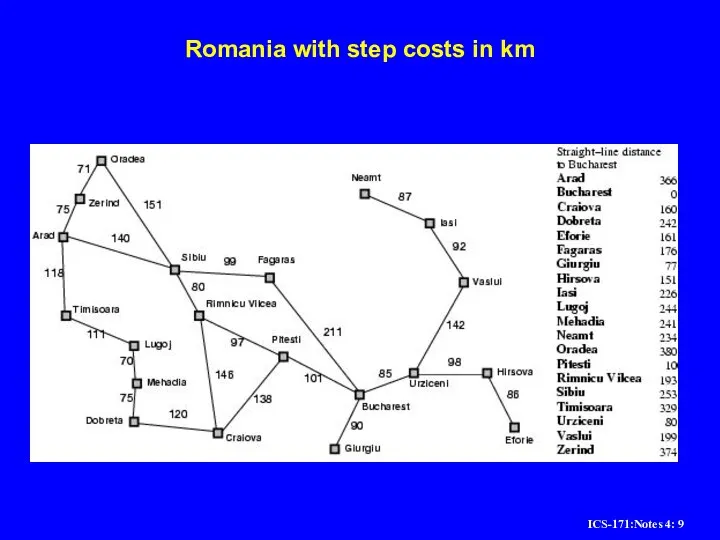
Слайд 9Romania with step costs in km
Слайд 10Greedy best-first search
Evaluation function f(n) = h(n) (heuristic)
= estimate of cost from

n to goal
e.g., hSLD(n) = straight-line distance from n to Bucharest
Greedy best-first search expands the node that appears to be closest to goal
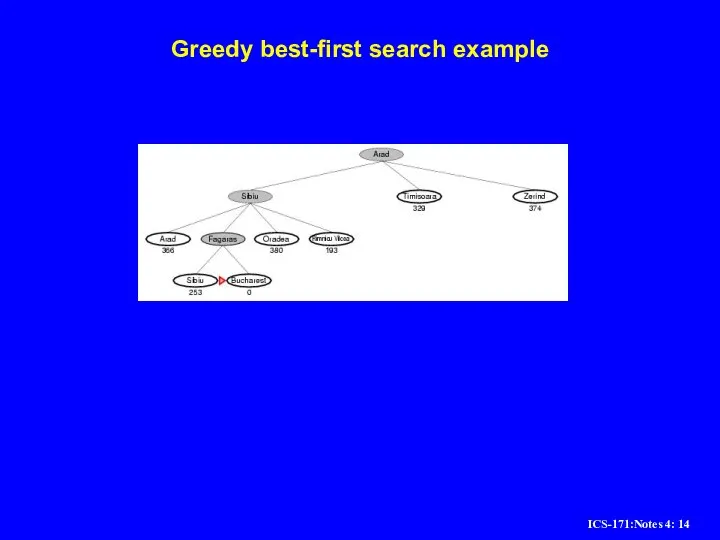
Слайд 11Greedy best-first search example

Слайд 12Greedy best-first search example

Слайд 13Greedy best-first search example

Слайд 14Greedy best-first search example
Слайд 15Problems with Greedy Search
Not complete
Get stuck on local minimas and plateaus,

Irrevocable,
Infinite loops
Can we incorporate heuristics in systematic search?
Слайд 16A* search
Idea: avoid expanding paths that are already expensive
Evaluation function f(n) =

g(n) + h(n)
g(n) = cost so far to reach n
h(n) = estimated cost from n to goal
f(n) = estimated total cost of path through n to goal
Слайд 23A*- a special Best-first search
Goal: find a minimum sum-cost path
Notation:
c(n,n’) - cost

of arc (n,n’)
g(n) = cost of current path from start to node n in the search tree.
h(n) = estimate of the cheapest cost of a path from n to a goal.
Special evaluation function: f = g+h
f(n) estimates the cheapest cost solution path that goes through n.
h*(n) is the true cheapest cost from n to a goal.
g*(n) is the true shortest path from the start s, to n.
If the heuristic function, h always underestimate the true cost (h(n) is smaller than h*(n)), then A* is guaranteed to find an optimal solution.
Слайд 24Admissible heuristics
A heuristic h(n) is admissible if for every node n,
h(n) ≤

h*(n), where h*(n) is the true cost to reach the goal state from n.
An admissible heuristic never overestimates the cost to reach the goal, i.e., it is optimistic
Example: hSLD(n) (never overestimates the actual road distance)
Theorem: If h(n) is admissible, A* using TREE-SEARCH is optimal
Слайд 28Algorithm A* (with any h on search Graph)
Input: a search graph problem

with cost on the arcs
Output: the minimal cost path from start node to a goal node.
1. Put the start node s on OPEN.
2. If OPEN is empty, exit with failure
3. Remove from OPEN and place on CLOSED a node n having minimum f.
4. If n is a goal node exit successfully with a solution path obtained by tracing back the pointers from n to s.
5. Otherwise, expand n generating its children and directing pointers from each child node to n.
For every child node n’ do
evaluate h(n’) and compute f(n’) = g(n’) +h(n’)= g(n)+c(n,n’)+h(n)
If n’ is already on OPEN or CLOSED compare its new f with the old f and attach the lowest f to n’.
put n’ with its f value in the right order in OPEN
6. Go to step 2.
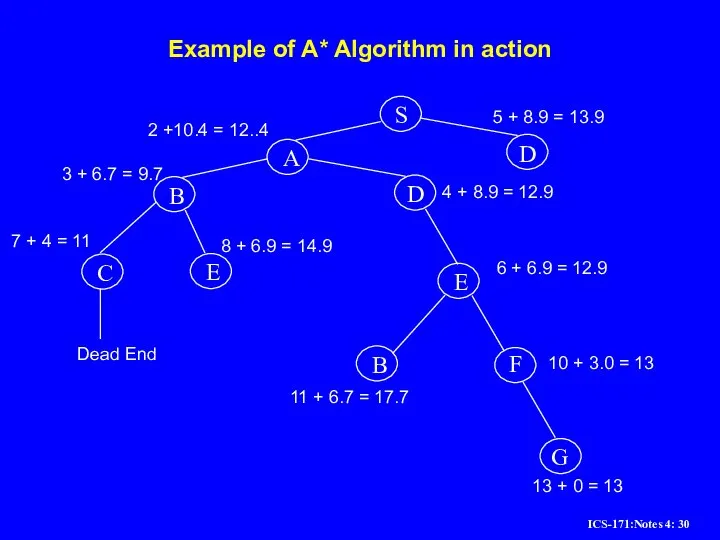
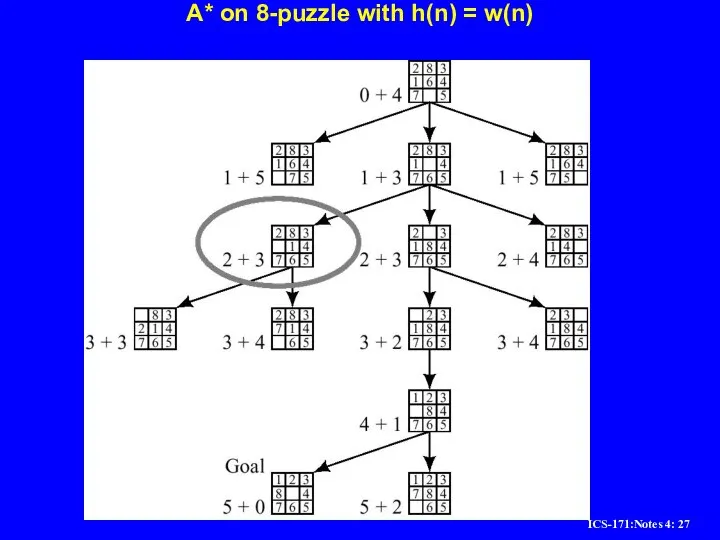
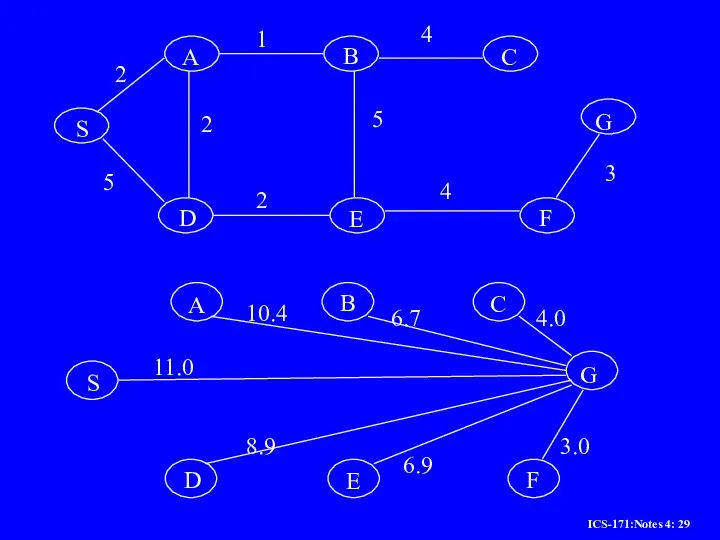
Слайд 30Example of A* Algorithm in action
S
A
D
B
D
C
E
E
B
F
G
2 +10.4 = 12..4
5 + 8.9 =
13.9
3 + 6.7 = 9.7
7 + 4 = 11
8 + 6.9 = 14.9
4 + 8.9 = 12.9
6 + 6.9 = 12.9
11 + 6.7 = 17.7
10 + 3.0 = 13
13 + 0 = 13
Dead End
Слайд 31Behavior of A* - Completeness
Theorem (completeness for optimal solution) (HNL, 1968):
If

the heuristic function is admissible than A* finds an optimal solution.
Proof:
1. A* will expand only nodes whose f-values are less (or equal) to the optimal cost path C* (f(n) less-or-equal c*).
2. The evaluation function of a goal node along an optimal path equals C*.
Lemma:
Anytime before A* terminates there exists and OPEN node n’ on an optimal path with f(n’) <= C*.
Слайд 33Consistent heuristics
A heuristic is consistent if for every node n, every successor

n' of n generated by any action a,
h(n) ≤ c(n,a,n') + h(n')
If h is consistent, we have
f(n') = g(n') + h(n')
= g(n) + c(n,a,n') + h(n')
≥ g(n) + h(n)
= f(n)
i.e., f(n) is non-decreasing along any path.
Theorem: If h(n) is consistent, A* using GRAPH-SEARCH is optimal
Слайд 34Optimality of A* with consistent h
A* expands nodes in order of increasing

f value
Gradually adds "f-contours" of nodes
Contour i has all nodes with f=fi, where fi < fi+1
Слайд 35Summary: Consistent (Monotone) Heuristics
If in the search graph the heuristic function satisfies

triangle inequality for every n and its child node n’: h^(ni) less or equal h^(nj) + c(ni,nj)
when h is monotone, the f values of nodes expanded by A* are never decreasing.
When A* selected n for expansion it already found the shortest path to it.
When h is monotone every node is expanded once (if check for duplicates).
Normally the heuristics we encounter are monotone
the number of misplaced ties
Manhattan distance
air-line distance
Слайд 36Admissible heuristics
E.g., for the 8-puzzle:
h1(n) = number of misplaced tiles
h2(n) = total

Manhattan distance
(i.e., no. of squares from desired location of each tile)
h1(S) = ?
h2(S) = ?
Слайд 37Admissible heuristics
E.g., for the 8-puzzle:
h1(n) = number of misplaced tiles
h2(n) = total
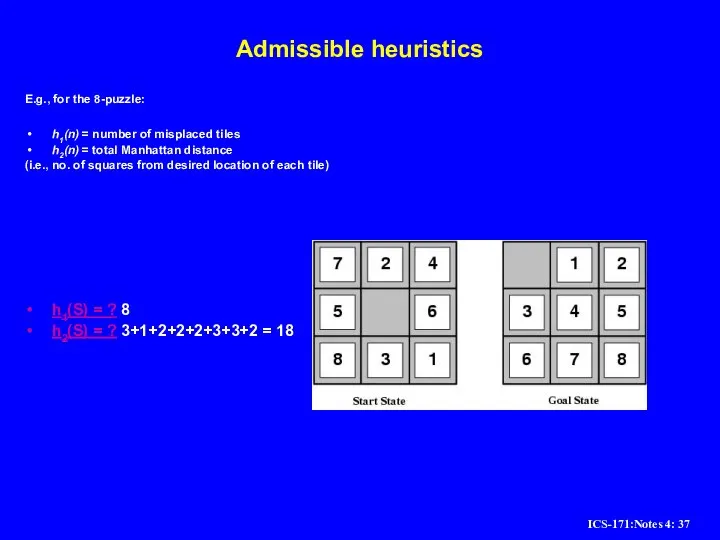
Manhattan distance
(i.e., no. of squares from desired location of each tile)
h1(S) = ? 8
h2(S) = ? 3+1+2+2+2+3+3+2 = 18
Слайд 38Dominance
If h2(n) ≥ h1(n) for all n (both admissible)
then h2 dominates h1

h2 is better for search
Typical search costs (average number of nodes expanded):
d=12 IDS = 3,644,035 nodes
A*(h1) = 227 nodes A*(h2) = 73 nodes
d=24 IDS = too many nodes
A*(h1) = 39,135 nodes A*(h2) = 1,641 nodes
Слайд 39Complexity of A*
A* is optimally efficient (Dechter and Pearl 1985):
It can be

shown that all algorithms that do not expand a node which A* did expand (inside the contours) may miss an optimal solution
A* worst-case time complexity:
is exponential unless the heuristic function is very accurate
If h is exact (h = h*)
search focus only on optimal paths
Main problem: space complexity is exponential
Effective branching factor:
logarithm of base (d+1) of average number of nodes expanded.
Слайд 40Effectiveness of A* Search Algorithm
d IDS A*(h1) A*(h2)
2 10 6 6
4 112 13 12
8 6384 39 25
12 364404 227 73
14 3473941 539 113
20 ------------ 7276 676
Average number of nodes expanded
Average over 100 randomly

generated 8-puzzle problems
h1 = number of tiles in the wrong position
h2 = sum of Manhattan distances
Слайд 41Properties of A*
Complete? Yes (unless there are infinitely many nodes with f

≤ f(G) )
Time? Exponential
Space? Keeps all nodes in memory
Optimal? Yes
A* expands all nodes having f(n) < C*
A* expands some nodes having f(n) = C*
A* expands no nodes having f(n) > C*
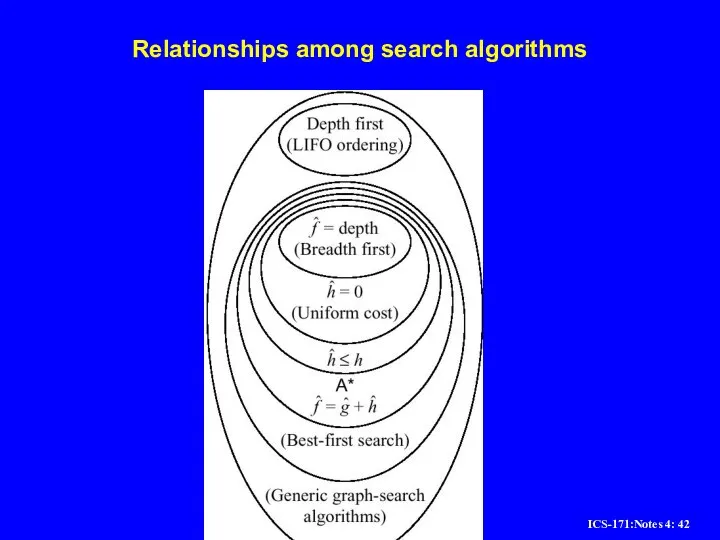
Слайд 42Relationships among search algorithms
Слайд 43Pseudocode for Branch and Bound Search
(An informed depth-first search)
Initialize: Let Q =

{S}
While Q is not empty
pull Q1, the first element in Q
if Q1 is a goal compute the cost of the solution and update
L <-- minimum between new cost and old cost
else
child_nodes = expand(Q1),
,
For each child node n do:
evaluate f(n). If f(n) is greater than L discard n.
end-for
Put remaining child_nodes on top of queue in the order of their evaluation function, f.
end
Continue
Слайд 44Properties of Branch-and-Bound
Not guaranteed to terminate unless has depth-bound
Optimal:
finds an optimal

solution
Time complexity: exponential
Space complexity: linear
Слайд 45Iterative Deepening A* (IDA*)
(combining Branch-and-Bound and A*)
Initialize: f <-- the evaluation function

of the start node
until goal node is found
Loop:
Do Branch-and-bound with upper-bound L equal current evaluation function
Increment evaluation function to next contour level
end
continue
Properties:
Guarantee to find an optimal solution
time: exponential, like A*
space: linear, like B&B.
Слайд 47Inventing Heuristics automatically
Examples of Heuristic Functions for A*
the 8-puzzle problem
the number of

tiles in the wrong position
is this admissible?
the sum of distances of the tiles from their goal positions, where distance is counted as the sum of vertical and horizontal tile displacements (“Manhattan distance”)
is this admissible?
How can we invent admissible heuristics in general?
look at “relaxed” problem where constraints are removed
e.g.., we can move in straight lines between cities
e.g.., we can move tiles independently of each other
Слайд 48Inventing Heuristics Automatically (continued)
How did we
find h1 and h2 for the

8-puzzle?
verify admissibility?
prove that air-distance is admissible? MST admissible?
Hypothetical answer:
Heuristic are generated from relaxed problems
Hypothesis: relaxed problems are easier to solve
In relaxed models the search space has more operators, or more directed arcs
Example: 8 puzzle:
A tile can be moved from A to B if A is adjacent to B and B is clear
We can generate relaxed problems by removing one or more of the conditions
A tile can be moved from A to B if A is adjacent to B
...if B is blank
A tile can be moved from A to B.
Слайд 49Generating heuristics (continued)
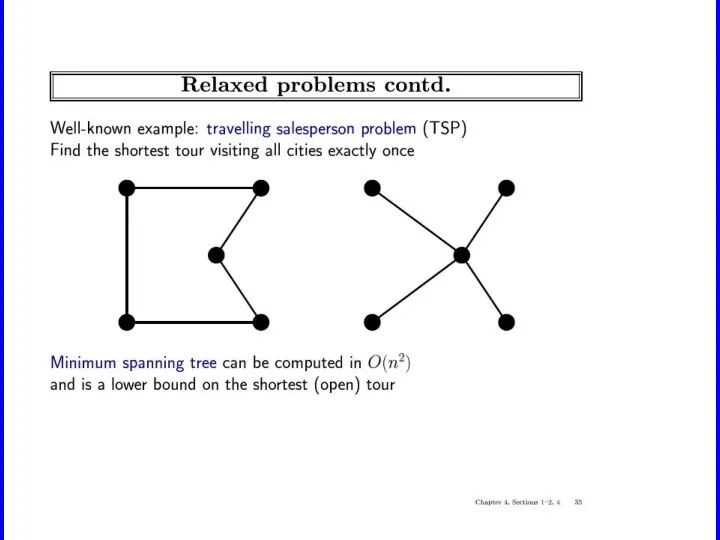
Example: TSP
Finr a tour. A tour is:
1. A graph
2. Connected
3.

Each node has degree 2.
Eliminating 2 yields MST.
Слайд 50Relaxed problems
A problem with fewer restrictions on the actions is called a

relaxed problem
The cost of an optimal solution to a relaxed problem is an admissible heuristic for the original problem
If the rules of the 8-puzzle are relaxed so that a tile can move anywhere, then h1(n) gives the shortest solution
If the rules are relaxed so that a tile can move to any adjacent square, then h2(n) gives the shortest solution
Слайд 52Automating Heuristic generation
Use Strips representation:
Operators:
Pre-conditions, add-list, delete list
8-puzzle example:
On(x,y), clear(y) adj(y,z) ,tiles

x1,…,x8
States: conjunction of predicates:
On(x1,c1),on(x2,c2)….on(x8,c8),clear(c9)
Move(x,c1,c2) (move tile x from location c1 to location c2)
Pre-cond: on(x1.c1), clear(c2), adj(c1,c2)
Add-list: on(x1,c2), clear(c1)
Delete-list: on(x1,c1), clear(c2)
Relaxation:
1. Remove from prec-dond: clear(c2), adj(c2,c3) ? #misplaced tiles
2. Remove clear(c2) ? manhatten distance
3. Remove adj(c2,c3) ? h3, a new procedure that transfer to the empty location a tile appearing there in the goal
Слайд 53Heuristic generation
The space of relaxations can be enriched by predicate refinements
Adj(y,z) iff

neigbour(y,z) and same-line(y,z)
The main question: how to recognize a relaxed problem which is easy.
A proposal:
A problem is easy if it can be solved optimally by agreedy algorithm
Heuristics that are generated from relaxed models are monotone.
Proof: h is true shortest path I relaxed model
H(n) <=c’(n,n’)+h(n’)
C’(n,n’) <=c(n,n’)
? h(n) <= c(n,n’)+h(n’)
Problem: not every relaxed problem is easy, often, a simpler problem which is more constrained will provide a good upper-bound.
Слайд 54Improving Heuristics
If we have several heuristics which are non dominating we can

select the max value.
Reinforcement learning.
Слайд 55Local search algorithms
In many optimization problems, the path to the goal is

irrelevant; the goal state itself is the solution
State space = set of "complete" configurations
Find configuration satisfying constraints, e.g., n-queens
In such cases, we can use local search algorithms
keep a single "current" state, try to improve it
Constant space. Good for offline and online search
Слайд 57Hill-climbing search
"Like climbing Everest in thick fog with amnesia"

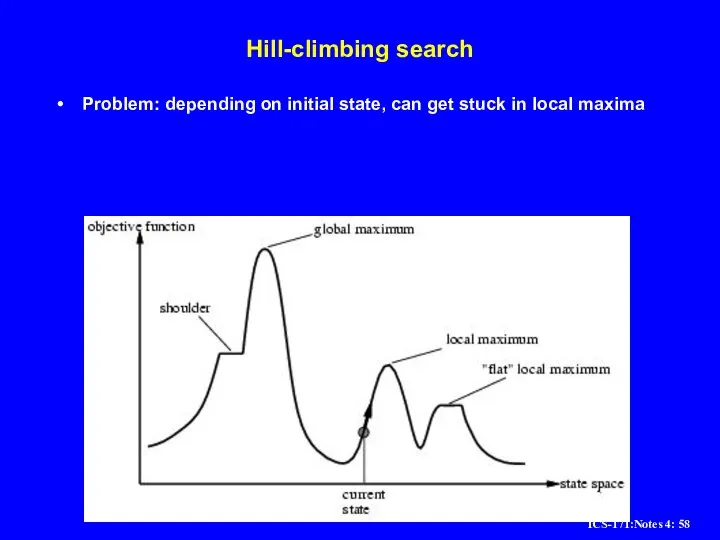
Слайд 58Hill-climbing search
Problem: depending on initial state, can get stuck in local maxima
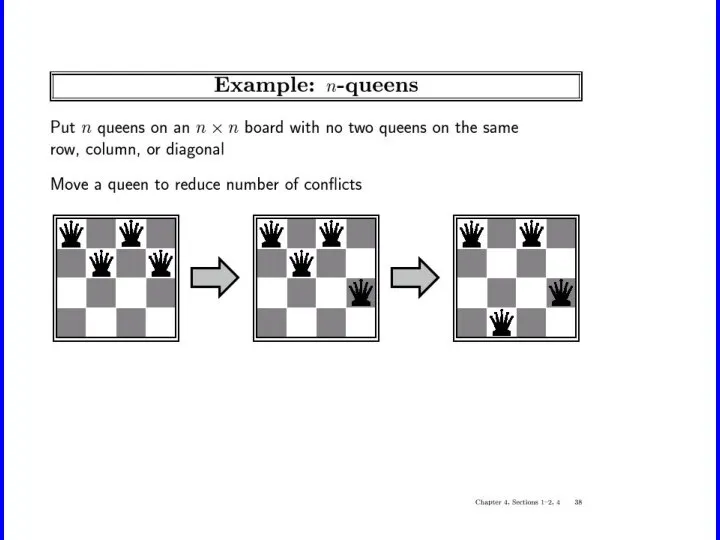
Слайд 59Hill-climbing search: 8-queens problem
h = number of pairs of queens that are

attacking each other, either directly or indirectly
h = 17 for the above state
Слайд 60Hill-climbing search: 8-queens problem
A local minimum with h = 1

Слайд 61Simulated annealing search
Idea: escape local maxima by allowing some "bad" moves but

gradually decrease their frequency























































 Факторы, влияющие на скорость химических реакций
Факторы, влияющие на скорость химических реакций Презентация на тему Сосновый лес
Презентация на тему Сосновый лес  Деятельность учителя начальных классов в рамках ФГОС
Деятельность учителя начальных классов в рамках ФГОС Где прячутся взрывчатые вещества
Где прячутся взрывчатые вещества Урок русского языка в 5 классе
Урок русского языка в 5 классе Simul'ONU
Simul'ONU Тема учебного проекта:
Тема учебного проекта: Щелочные металлы
Щелочные металлы МИМ № 22«Лунный месяц»
МИМ № 22«Лунный месяц» Иконостас - алтарная перегородка, с установленными на ней в несколько рядов иконами в определенном порядке
Иконостас - алтарная перегородка, с установленными на ней в несколько рядов иконами в определенном порядке Профессиональные ценности журналиста
Профессиональные ценности журналиста  Профессия водолаз
Профессия водолаз Название инструмента
Название инструмента Слово господа. Сирах 10:4 2-е Петра 3:18 Псалмов15:3
Слово господа. Сирах 10:4 2-е Петра 3:18 Псалмов15:3 Русская изба. Экскурсия в музей
Русская изба. Экскурсия в музей Летопись победного года 1945 год вошел в историю Великой Отечественной войны и второй мировой войны в целом как год завершающих сраж
Летопись победного года 1945 год вошел в историю Великой Отечественной войны и второй мировой войны в целом как год завершающих сраж Инвентарь горничной
Инвентарь горничной География Челябинской области 9 класс.Транспорт и экология Челябинской области.
География Челябинской области 9 класс.Транспорт и экология Челябинской области. 2 Авторский коллектив Преподаватели кафедры общей физики физического факультета МГУ им. М.В. Ломоносова: Грачев А.В., к.ф.-м.н., доцент
2 Авторский коллектив Преподаватели кафедры общей физики физического факультета МГУ им. М.В. Ломоносова: Грачев А.В., к.ф.-м.н., доцент Праздники Швейцарии
Праздники Швейцарии Права человека
Права человека MVVM Adobe Flex
MVVM Adobe Flex Электроника
Электроника Prezentatsia_s_fonom_univera
Prezentatsia_s_fonom_univera Книжный магазин Knowledge
Книжный магазин Knowledge  Звездочёт
Звездочёт Агентская схема
Агентская схема ЭТАПЫ РАЗРАБОТКИ ПРОГРАММЫ
ЭТАПЫ РАЗРАБОТКИ ПРОГРАММЫ