Содержание
- 2. Introduction One of the most important applications of statics, in the analysis of problems involving mechanics
- 3. Objectives: Determine the characteristics of external forces. Develop a technique to analyze the resultant internal forces
- 4. External Forces In reality, the structures under investigation may be subjected to very complicated loadings in
- 5. Pressure Distribution Over a Flat Surface The external force is described by the load function p
- 6. This resultant force can be represented as shown below: The location where FR acts on the
- 7. Pressure distribution can be caused by wind, fluid, weights of objects etc. The intensity of the
- 8. The following example shows a typical distributed loading.
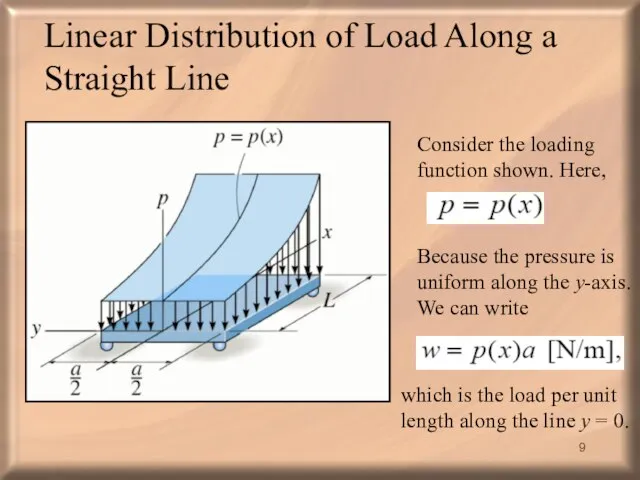
- 9. Linear Distribution of Load Along a Straight Line Consider the loading function shown. Here, Because the
- 10. The three-dimensional problem is now reduced to a two-dimensional problem, as shown. The resultant force is
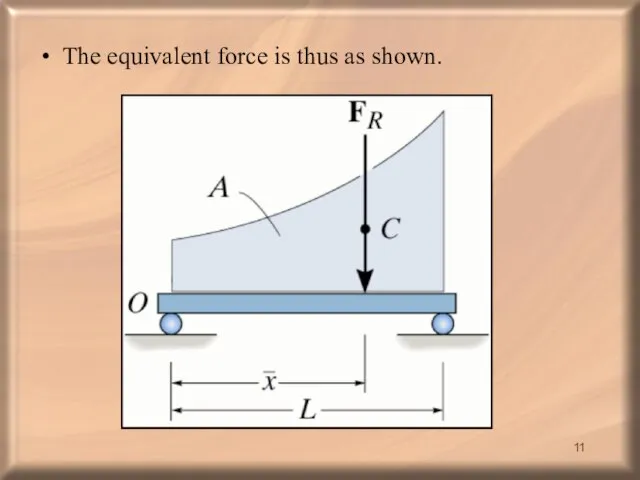
- 11. The equivalent force is thus as shown.
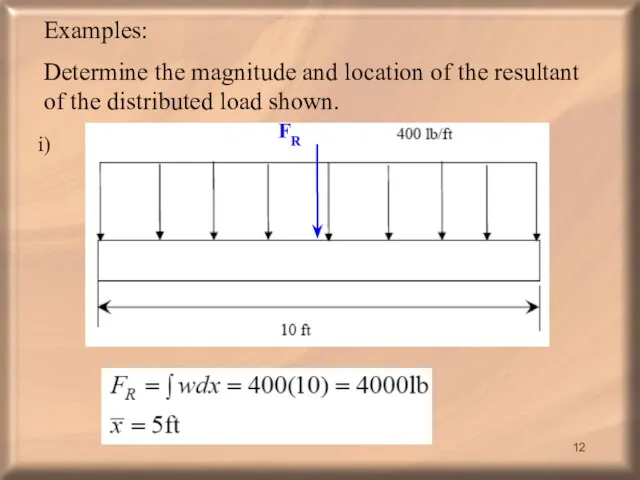
- 12. Examples: Determine the magnitude and location of the resultant of the distributed load shown. i)
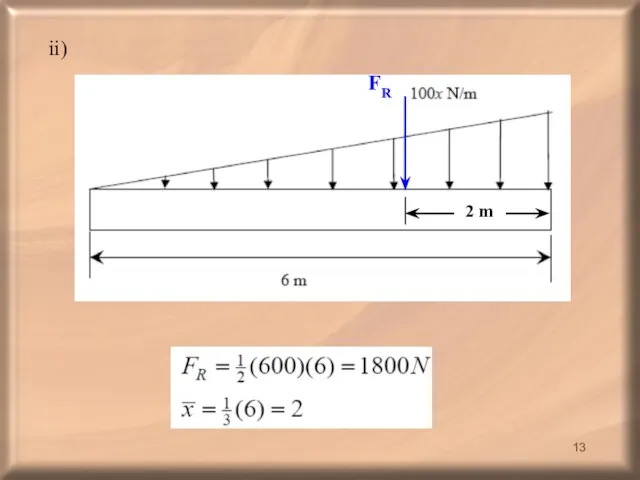
- 13. ii) 2 m
- 14. Example: Determine the magnitude and resultant of the loading acting on the beam.
- 15. Solution: Divide the trapezoidal loading into rectangle and triangle loading.
- 16. The equivalent position can be found as Vertical force equilibrium requires: To find the equivalent point
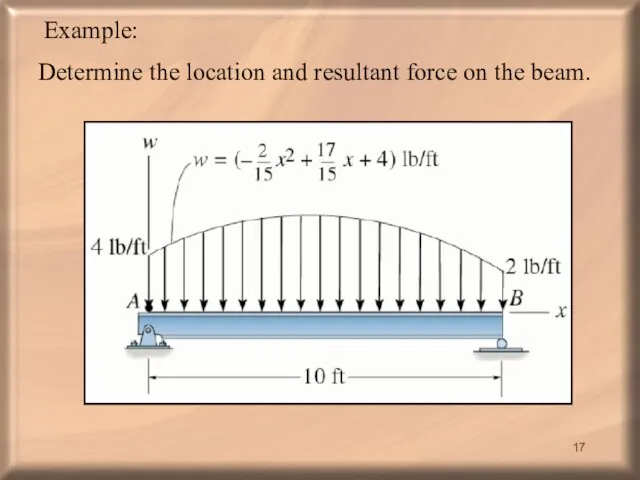
- 17. Example: Determine the location and resultant force on the beam.
- 18. FR = 52.222 lb ft
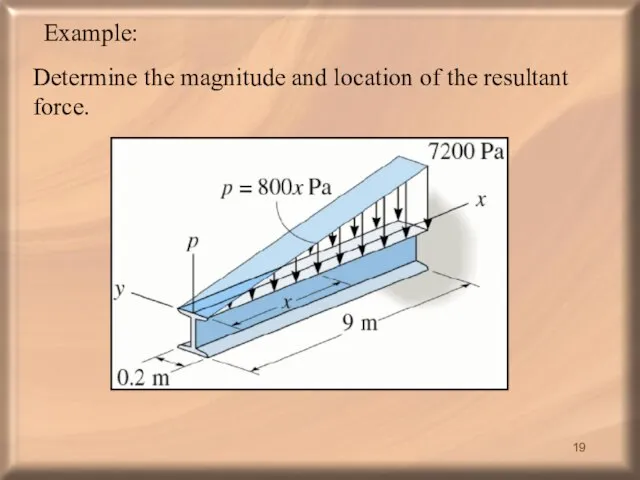
- 19. Example: Determine the magnitude and location of the resultant force.
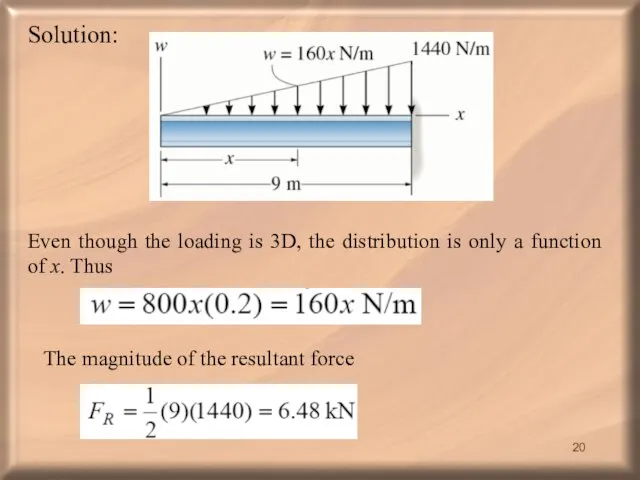
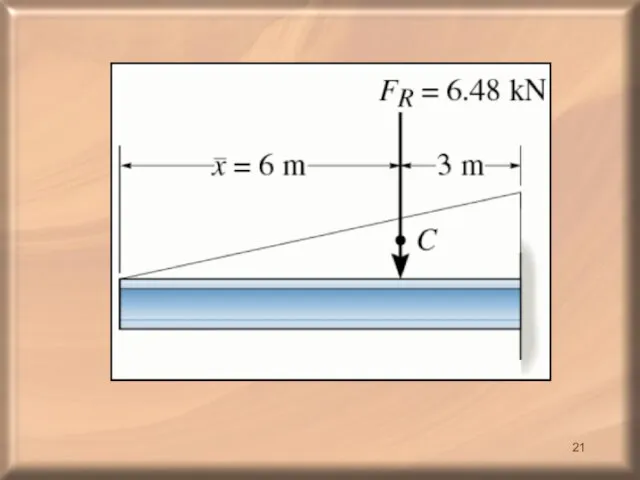
- 20. Solution: Even though the loading is 3D, the distribution is only a function of x. Thus
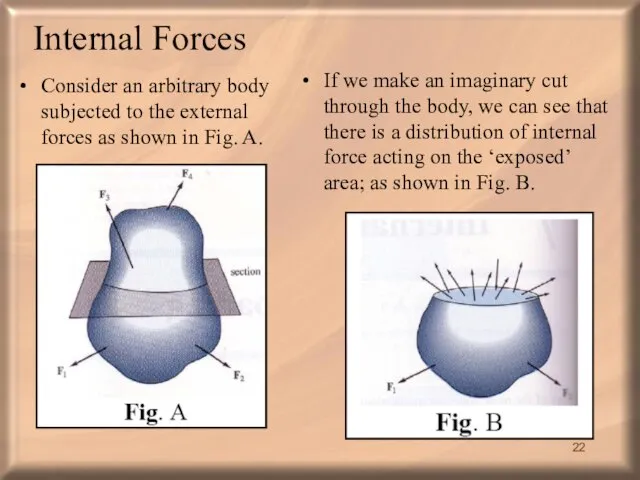
- 22. Internal Forces Consider an arbitrary body subjected to the external forces as shown in Fig. A.
- 23. These forces represent the effect of the material of the top part of the body acting
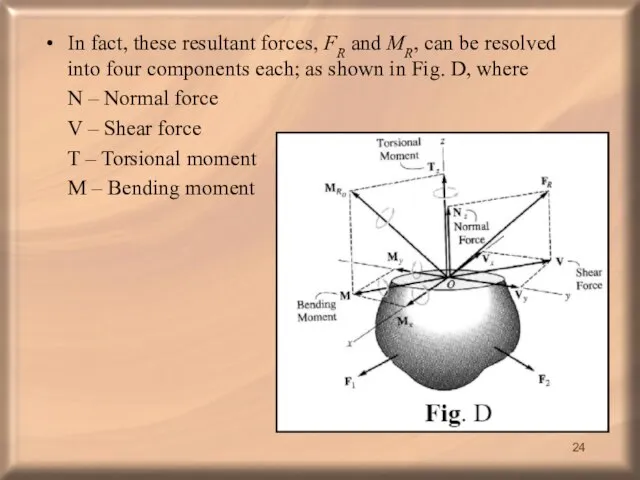
- 24. In fact, these resultant forces, FR and MR, can be resolved into four components each; as
- 25. For analysis of two dimensional bodies, it is sufficient to consider the normal force, shear force
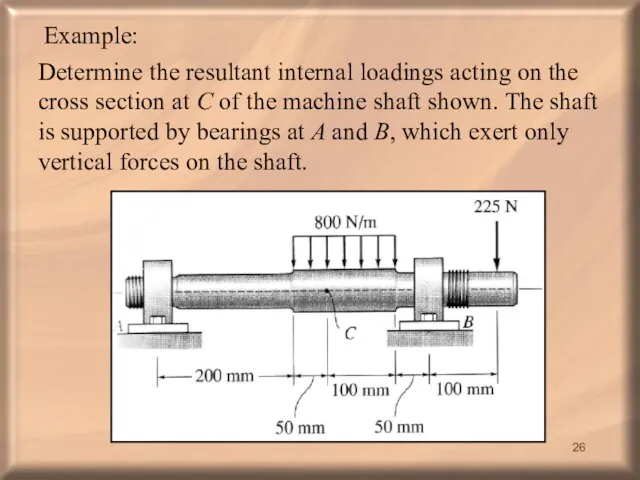
- 26. Example: Determine the resultant internal loadings acting on the cross section at C of the machine
- 27. Solution: First we need to obtain the reaction at the supports.
- 28. In order to analyze the resultant internal loading at C, we section the beam at C.
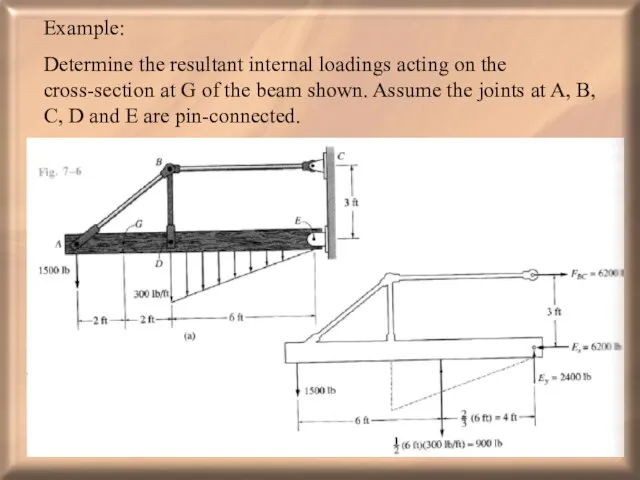
- 29. Example: Determine the resultant internal loadings acting on the cross-section at G of the beam shown.
- 30. But we cannot solve Cy and Ey. To proceed, if we look at beam AE, it
- 31. Next, we proceed to analyze joint B.
- 32. Finally we analyze segment AG
- 33. Extra Example Characteristics of External Loading
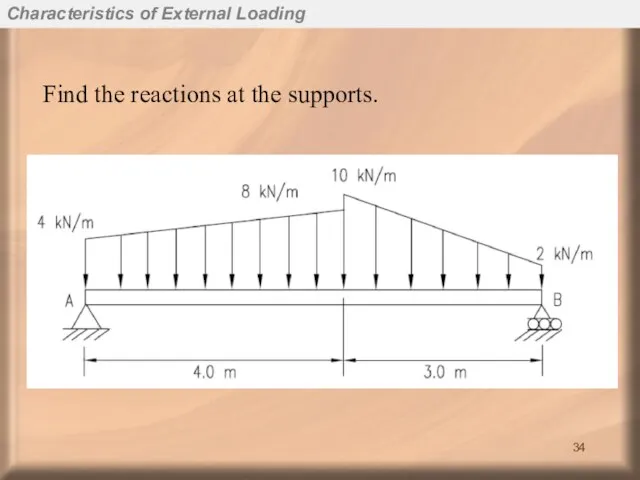
- 34. Find the reactions at the supports. Characteristics of External Loading
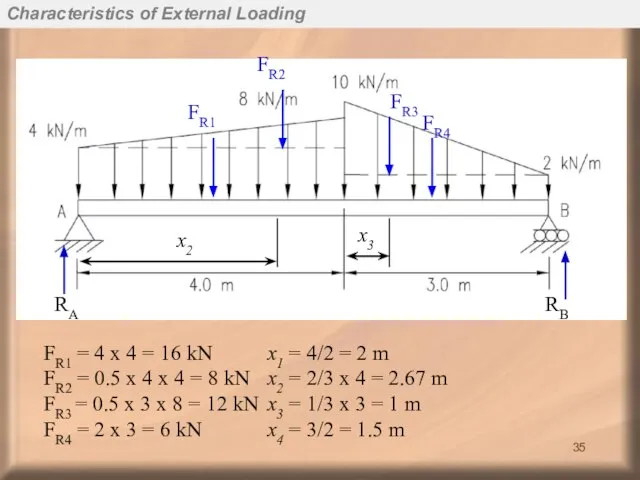
- 35. FR1 FR2 FR3 FR4 x2 x3 FR1 = 4 x 4 = 16 kN x1 =
- 37. Скачать презентацию




















 ООО Континент тур
ООО Континент тур Блудный сын
Блудный сын Правописание жи и ши
Правописание жи и ши Лекция №5. Особенности реконструкции дорожных одежд нежесткого типа
Лекция №5. Особенности реконструкции дорожных одежд нежесткого типа Япония Столица-город Токио
Япония Столица-город Токио Мочевыделительная система
Мочевыделительная система Strategic marketing
Strategic marketing Музеи искусства
Музеи искусства Финансирование плана развития организации образования
Финансирование плана развития организации образования Современное стрелковое оружие
Современное стрелковое оружие Зоогостиница Лесси
Зоогостиница Лесси Хостел Достоевский в центре Челябинска
Хостел Достоевский в центре Челябинска Псалом 9. Полны клятв слова его, уста полны лести и лжи
Псалом 9. Полны клятв слова его, уста полны лести и лжи Стандартизация. Общие положения стандартизации
Стандартизация. Общие положения стандартизации Десерт Шокомяч
Десерт Шокомяч ВИЧ и СПИД
ВИЧ и СПИД Фонды целевого капитала: состояние рынка Киев, 23 февраля 2012
Фонды целевого капитала: состояние рынка Киев, 23 февраля 2012 Афины и Спарта
Афины и Спарта Руководитель маркетинга как им быть или как им стать
Руководитель маркетинга как им быть или как им стать Гимнастика. Виды гимнастики
Гимнастика. Виды гимнастики Экономический рост
Экономический рост Информационные технологии в производстве авиационных двигателей УМПО
Информационные технологии в производстве авиационных двигателей УМПО Братья наши меньшие.
Братья наши меньшие. Кандалакшская районная организация профсоюза работников народного образования: публичный отчёт 2020
Кандалакшская районная организация профсоюза работников народного образования: публичный отчёт 2020 МЕТОДЫ УПРАВЛЕНИЯ
МЕТОДЫ УПРАВЛЕНИЯ Современная туристическая одежда
Современная туристическая одежда Профессия моей мамы
Профессия моей мамы Презентация на тему Одиссея Гомера (5 класс)
Презентация на тему Одиссея Гомера (5 класс)