трактата Архимеда о полуправильных выпуклых однородных многогранниках. Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра.
Модели И.Кеплера
Вклад Кеплера в теорию многогранника - это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра.


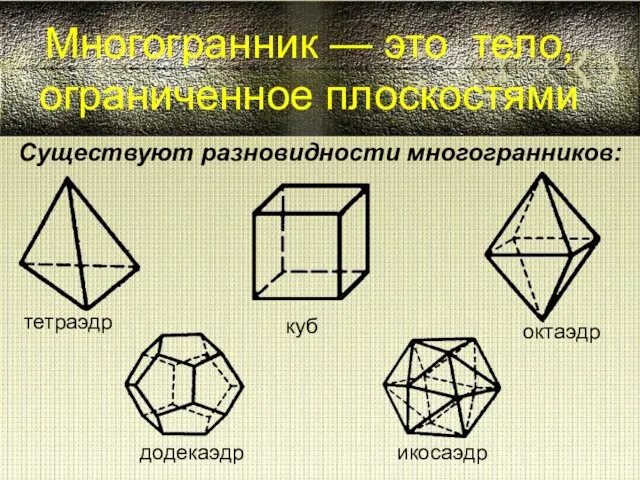
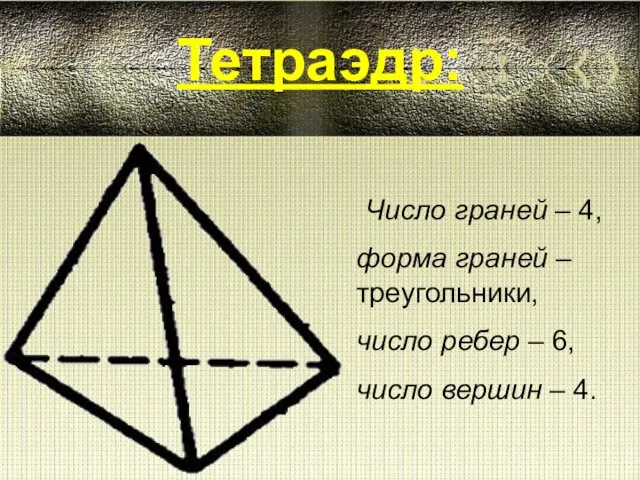
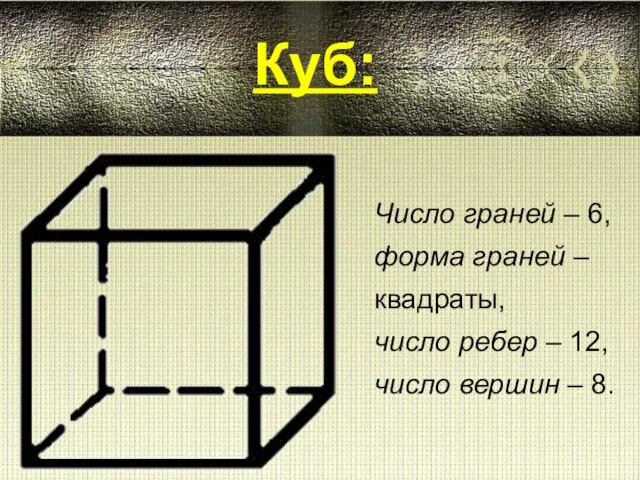
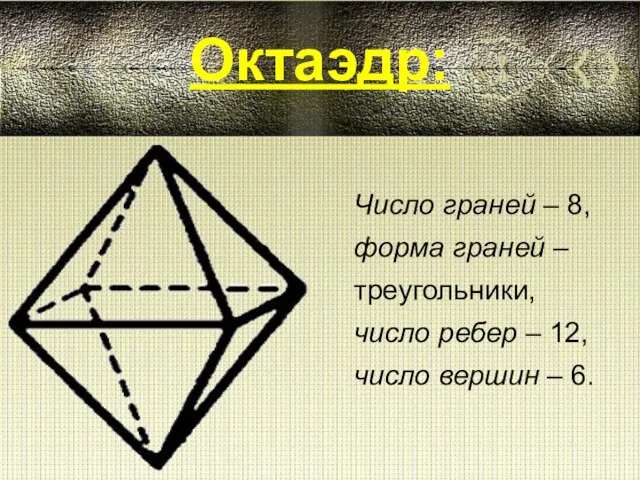





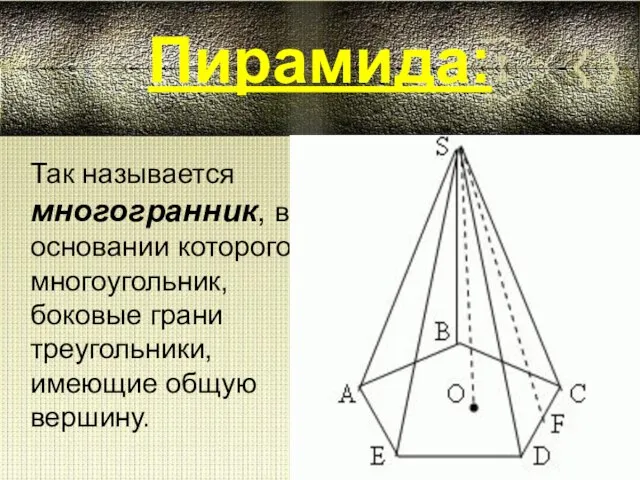
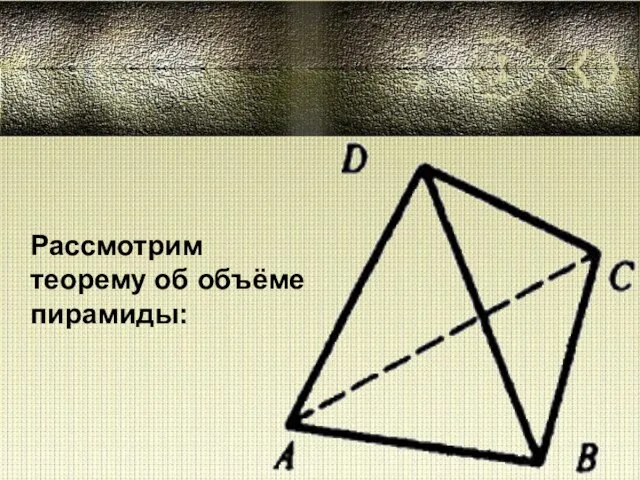

 History of English I
History of English I Рассылки против блоговКирилл Чистов
Рассылки против блоговКирилл Чистов Способ фильтрования воды
Способ фильтрования воды How big am i
How big am i ПРОЕКТ "Сетевой Ресурсный центр
ПРОЕКТ "Сетевой Ресурсный центр Ажурные снежинки
Ажурные снежинки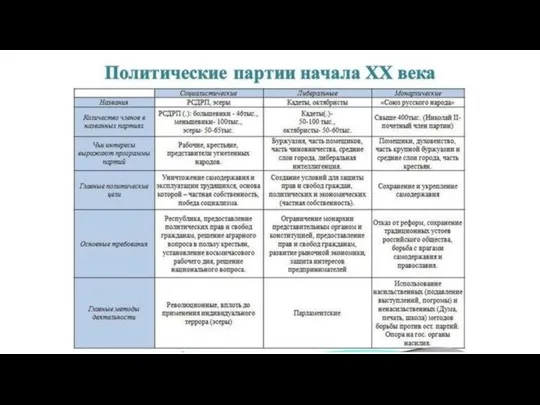 Политические партии начала ХХ века
Политические партии начала ХХ века Жить в Сибири. Сельский воркаут. КРОО Новый день
Жить в Сибири. Сельский воркаут. КРОО Новый день Презентация на тему Политические системы
Презентация на тему Политические системы О РАЗРАБОТКЕ СОДЕРЖАНИЯ ПРОФИЛЬНОЙ ПОДГОТОВКИ БАКАЛАВРОВ С ИСПОЛЬЗОВАНИЕМ ПРОФЕССИОНАЛЬНЫХ СТАНДАРТОВ ИТ-ОТРАСЛИ
О РАЗРАБОТКЕ СОДЕРЖАНИЯ ПРОФИЛЬНОЙ ПОДГОТОВКИ БАКАЛАВРОВ С ИСПОЛЬЗОВАНИЕМ ПРОФЕССИОНАЛЬНЫХ СТАНДАРТОВ ИТ-ОТРАСЛИ АМЕРИКАНСКИЕ УРОКИ
АМЕРИКАНСКИЕ УРОКИ Занятие 10
Занятие 10 С праздником. День Защиты детей
С праздником. День Защиты детей Ошибки в формах числа имен существительных
Ошибки в формах числа имен существительных Проект «Мобильные платежи»
Проект «Мобильные платежи» Презентация на тему строение скелета человека 4 класс
Презентация на тему строение скелета человека 4 класс  ИНСТРУМЕНТАРИЙДЛЯ ПЛАНИРОВАНИЯ И РЕШЕНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОБЛЕМ РЕГИОНАЛЬНОГО РАЗВИТИЯ И ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ
ИНСТРУМЕНТАРИЙДЛЯ ПЛАНИРОВАНИЯ И РЕШЕНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОБЛЕМ РЕГИОНАЛЬНОГО РАЗВИТИЯ И ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ История физики в вопросах
История физики в вопросах План на 2023 год
План на 2023 год 单词卡
单词卡 Гражданское законодательство
Гражданское законодательство Галактика ERP
Галактика ERP -1945 Презентацию подготовила Ларионова Е.Н. Учитель начальных классов МОУ «Гимназия» № 9
-1945 Презентацию подготовила Ларионова Е.Н. Учитель начальных классов МОУ «Гимназия» № 9 И как в рай, в Божий храм Запросилась душа
И как в рай, в Божий храм Запросилась душа GAP-анализ
GAP-анализ Ваша безопасность в наших руках
Ваша безопасность в наших руках Простые механизмы
Простые механизмы ЭЛЕКТИВНЫЕ КУРСЫ
ЭЛЕКТИВНЫЕ КУРСЫ