Исследование функций и построение графиков с помощью производной

«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…»
Н.И. Лобачевский
Скажи мне, и я забуду.
Покажи мне, и я запомню.
Дай мне действовать самому,
И я научусь.
Конфуций

Цели урока:
⮚ Образовательные.
Формировать:
- навыки прикладного использования аппарата производной;
- выявить уровень овладения учащимися комплексом знаний и умений по исследованию функции и ликвидировать пробелы в знаниях в соответствии с требованиями к математической подготовке учащихся.
⮚ Развивающие.
Развивать:
- способности к самостоятельному планированию и организации работы
- навыки коррекции собственной деятельности через применение информационных технологий;
- умение обобщать, абстрагировать и конкретизировать знания при исследовании функции.
⮚ Воспитательные.
Воспитывать:
- познавательный интерес к математике;
- информационную культуру и культуру общения;
- самостоятельность, способность к коллективной работе.

I этап. Актуализация ЗУН, необходимых для творческого применения знаний
Необходимое условие возрастания и убывания функции
Достаточное условие возрастания и убывания функции
Необходимое условие экстремума. (теорема Ферма)
Признак максимума функции.
Признак минимума функции.
Достаточные условия выпуклости и вогнутости графика функции

Необходимое условие возрастания и убывания функции
Т е о р е м а. Если дифференцируемая функция f(x), х∈(а;b), возрастает (убывает) на (а;b), то f `(x) ≥ 0 (f `(x) ≤ 0) для любого х из интервала (а;b).

Достаточные условия возрастания и убывания функции
Теорема Лагранжа.
Если функция f(x), х∈[а;b], непрерывна на отрезке [а;b] и дифференцируема на интервале (а;b), то найдётся точка с∈(а;b) такая, что имеет место формула
f(a) – f(b) = f `(c)(b – a)

Достаточное условие возрастания функции
Теорема. Если функция f имеет неотрицательную производную в каждой точке интервала (а;b), то функция f возрастает на интервале (а;b).

Достаточное условие убывания функции
Теорема. Если функция имеет неположительную производную в каждой точке интервала (а;b), то функция f убывает на интервале (а;b).

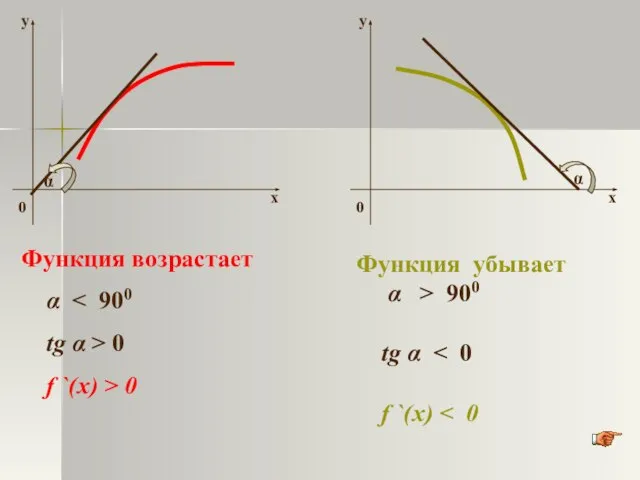
α
α
Функция возрастает
α < 900
tg α > 0
f `(x) > 0
Функция убывает
α > 900
tg α < 0
f `(x) < 0

Правило нахождения интервалов монотонности
1) Вычисляем производную f `(x) данной функции f(x), а затем находим точки, в которых f `(x) равна нулю или не существует. Эти точки называются критическими для функции f(x)

Правило нахождения интервалов монотонности
2) Критическими точками область определения функции f(x) разбивается на интервалы, на каждом из которых производная f `(x) сохраняет свой знак. Эти интервалы будут интервалами монотонности.

Правило нахождения интервалов монотонности
3) Определим знак f `(x) на каждом из найденных интервалов. Если на рассматриваемом интервале f `(x) ≥ 0, то на этом интервале f(x) возрастает, если же f `(x) ≤ 0, то на таком интервале f(x) убывает.

Исследование экстремумов функции
Необходимое условие экстремума.
(теорема Ферма)
Если точка х0 является точкой экстремума функции f и в этой точке существует производная f `(x), то она равна нулю:
f `(x) = 0.

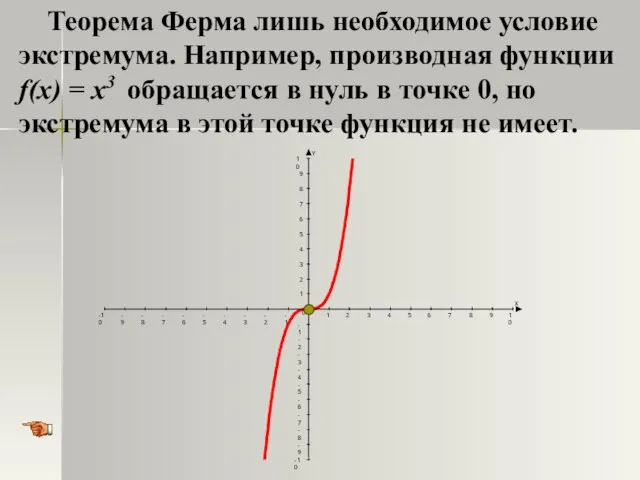
Теорема Ферма лишь необходимое условие экстремума. Например, производная функции f(x) = x3 обращается в нуль в точке 0, но экстремума в этой точке функция не имеет.
0

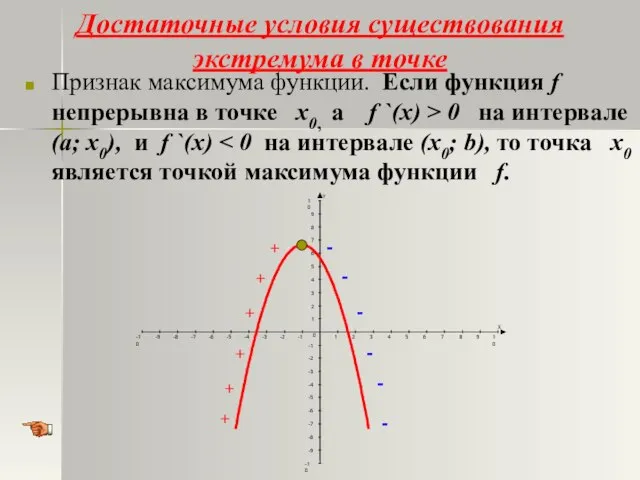
Достаточные условия существования экстремума в точке
Признак максимума функции. Если функция f непрерывна в точке х0, а f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.

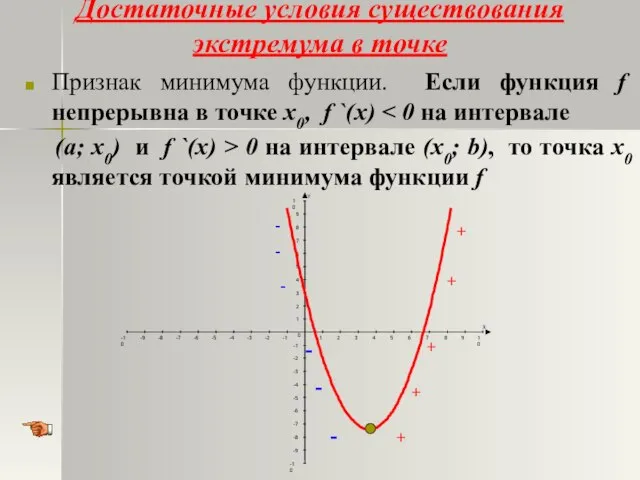
Достаточные условия существования экстремума в точке
Признак минимума функции. Если функция f непрерывна в точке х0, f `(x) < 0 на интервале
(а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f
X
Y
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
0

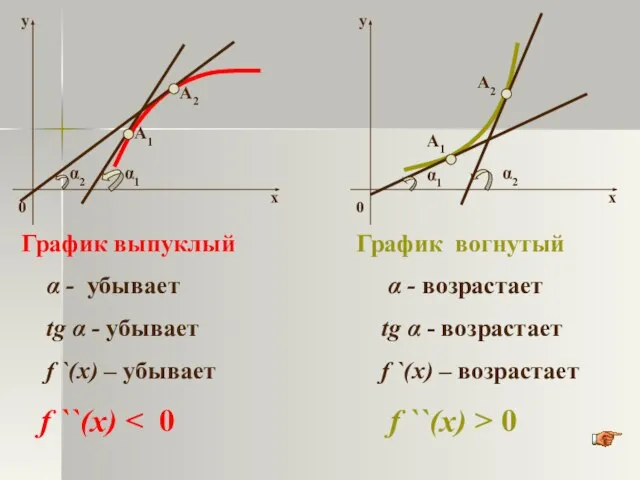
Достаточные условия выпуклости и вогнутости графика функции
Т е о р е м а. Пусть функция f(x), х∈(а;b), имеет первую и вторую производные. Тогда, если f ``(x) < 0 для всех х∈(а;b), то на интервале (а;b) график функции f(x) выпуклый вверх, если же f ``(x) > 0 для всех х∈(а;b), то график функции f(x) выпуклый вниз на (а;b).

α1
α2
График выпуклый
α - убывает
tg α - убывает
f `(x) – убывает
f ``(x) < 0
График вогнутый
α - возрастает
tg α - возрастает
f `(x) – возрастает
f ``(x) > 0
α1
α2
A1
A2
A1
A2

Точки перегиба
Найти критические точки функции по второй производной.
Исследовать знак второй производной в некоторой окрестности критический точки.
Если f ``(х) меняет свой знак при переходе аргумента через критическую точку х0, то (х0; f(х0)) - точка перегиба графика данной функции

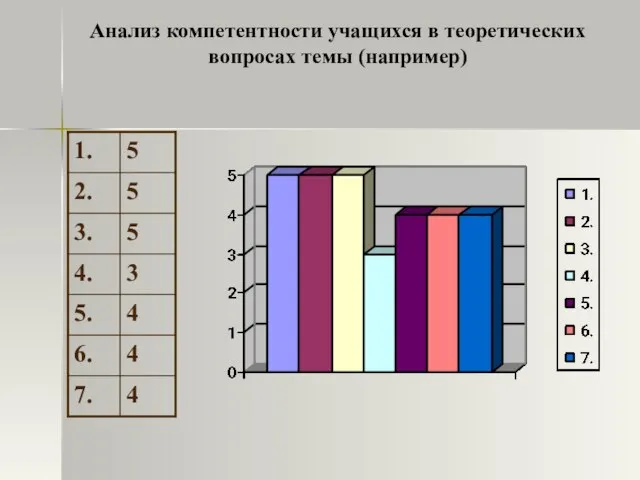
Анализ компетентности учащихся в теоретических вопросах темы (например)

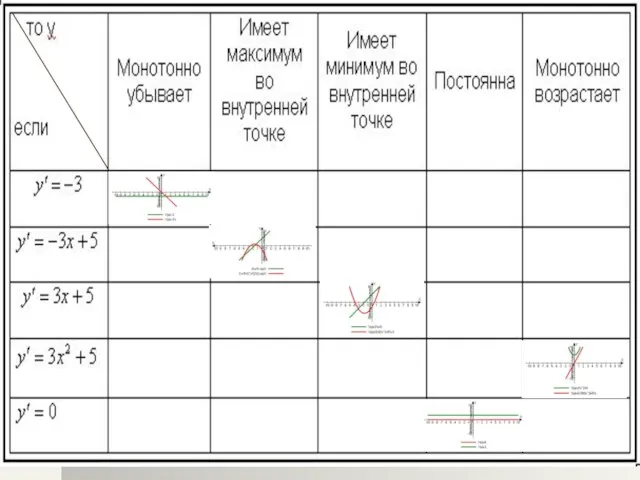
Заполните таблицу
Задание для всех учащихся.
II этап. Обобщение и систематизация знаний и способов деятельности

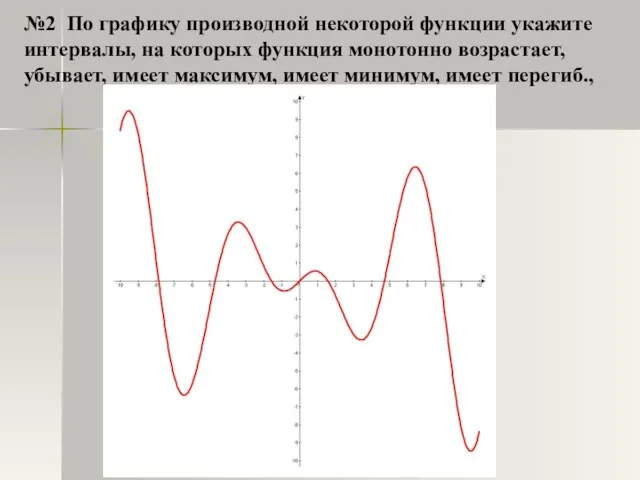
№2 По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет максимум, имеет минимум, имеет перегиб.,

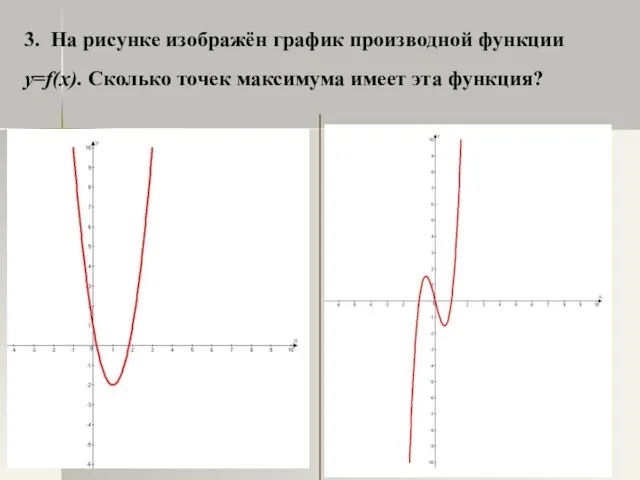
3. На рисунке изображён график производной функции y=f(x). Сколько точек максимума имеет эта функция?

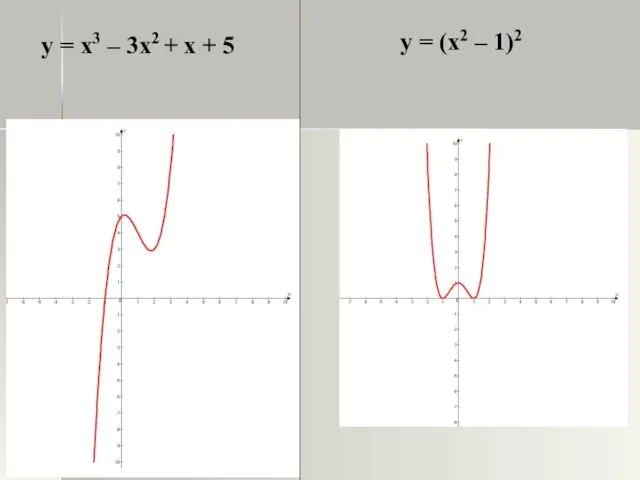
у = x3 – 3x2 + x + 5
у = (x2 – 1)2

III этап. Усвоение образца комплексного применения ЗУН.
Практическая работа с применением электронного учебного пособия «Математика – практикум 5-11» и по индивидуальным заданиям на местах.
За компьютер сначала рассаживаются 7 учащихся, остальные за парты. По мере выполнения заданий ребята меняются местами.

Работа на компьютере
Работа на местах

Работа с ЭУП «Математика – практикум
5-11»

Работа на компьютере

Какая из данных функций убывает на всей оси?

Исследовать функцию на выпуклость, вогнутость.

Ещё расскажу, если вам интересно,
Что точку разрыва и корень имею,
И есть интервал, где расти не посмею.
Во всём остальном положительна, право,
И это, конечно, не ради забавы.
Для чисел больших я стремлюсь к единице.
Найдите меня среди прочих в таблице.