Исследовательская группа«Землемеры»

Цели исследования
Выявить зависимость между периметрами фигур и их площадью.
Гипотеза
Чем больше периметр, тем больше площадь фигуры.
Что нужно выяснить:
Какие свойства периметра и площади фигур?
Как связаны периметры и площади прямоугольников?
Какая фигура имеет наибольшую площадь при заданном периметре?
Какие единицы измерения площади используются для измерения земли?

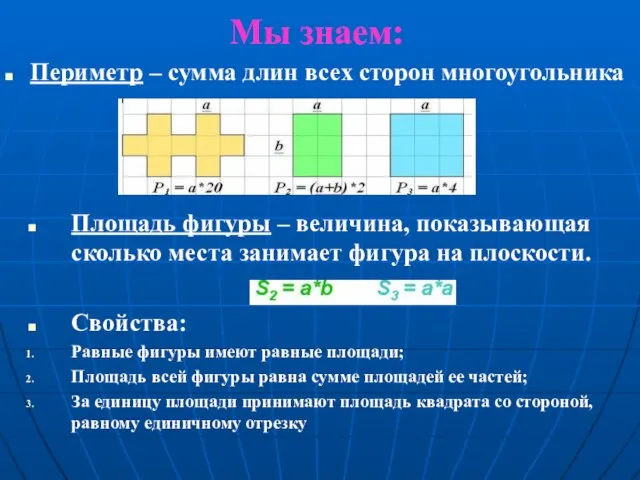
Мы знаем:
Периметр – сумма длин всех сторон многоугольника
Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.
Свойства:
Равные фигуры имеют равные площади;
Площадь всей фигуры равна сумме площадей ее частей;
За единицу площади принимают площадь квадрата со стороной, равному единичному отрезку

Если у одой фигуры больше периметр, чем у второй, то ее площадь больше, меньше или по-разному?
Заметили, если периметр одного прямоугольника больше, то и его площадь больше чем у других.
Но если периметры равны то площади могут быть различны
От чего зависят площади прямоугольников, если их периметры равны?
Сначала мы рассмотрим прямоугольники

“Какой из всех прямоугольников заданного периметра имеет наибольшую площадь?”
Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в книге Евклида, где доказывается, что, если рассмотреть прямоугольник и квадрат одного и того же периметра, то площадь квадрата будет больше.

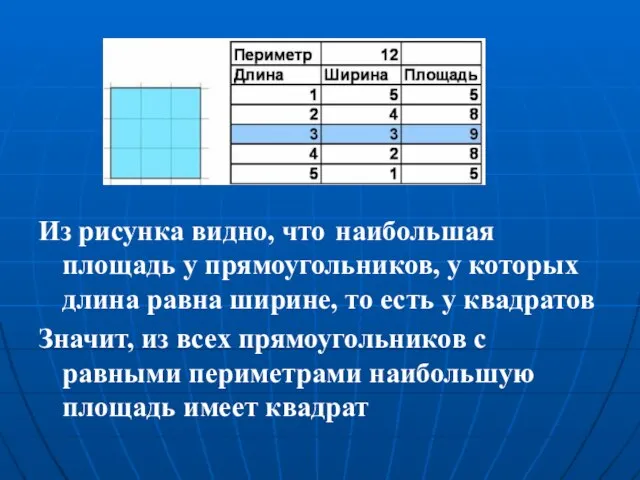
Из рисунка видно, что наибольшая площадь у прямоугольников, у которых длина равна ширине, то есть у квадратов
Значит, из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат

Как Пахом покупал землю (Задача Льва Толстого)
- А цена какая будет?- говорит Пахом.
Цена у нас одна: 1000 руб.за день.
Не понял Пахом.
- Какая же это мера – день? Сколько в ней десятин будет?
Мы этого, - говорит, не умеем считать. А мы за день продаем: сколько обойдешь в день, то и твое, а цена дню 100 рублей… Какой хочешь круг забирай, только до захода солнца приходи к тому месту, с какого взялся. Что обойдешь все твое
Какой путь должен выбрать Пахом, чтобы получить большую площадь земли?

Какой путь должен выбрать Пахом, чтобы получить большую площадь земли?
Теперь мы знаем, что Пахом должен идти по сторонам квадрата
А какие еще есть единицы площади?

Для измерения земли используются следующие единицы:
Метрические единицы площади
100 квадратных метров – а (ар):
1 ар = 100 м2;
Квадрат со стороной 100 метров –
га (гектар):
1 га = 10000 м2;
Неметрические единицы площади

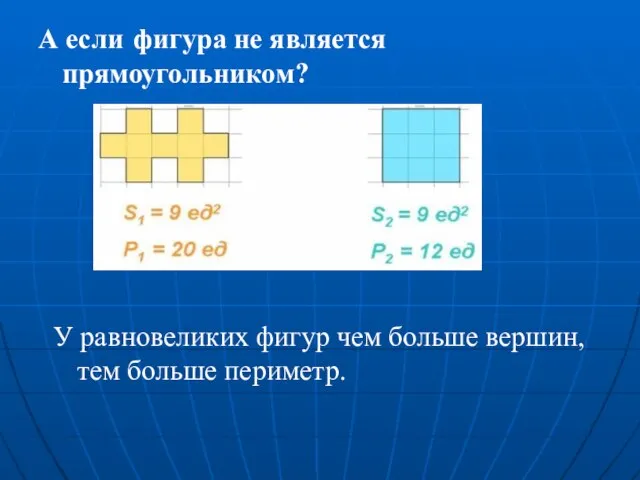
А если фигура не является прямоугольником?
У равновеликих фигур чем больше вершин, тем больше периметр.