Измерения в психологии

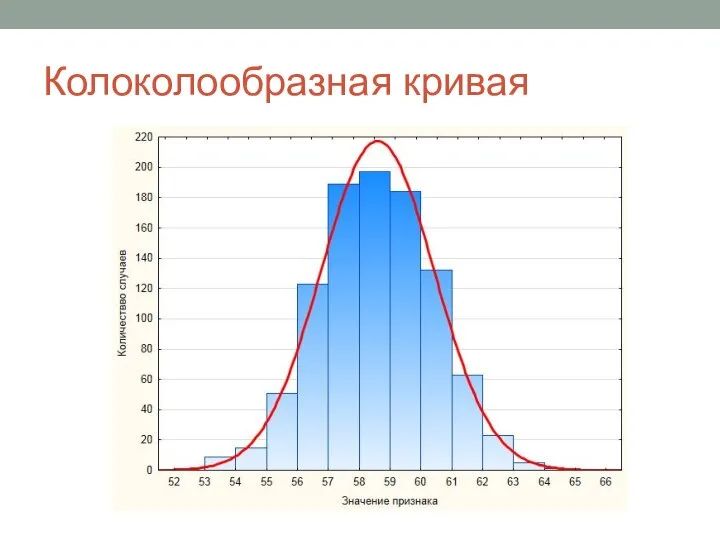
Колоколообразная кривая

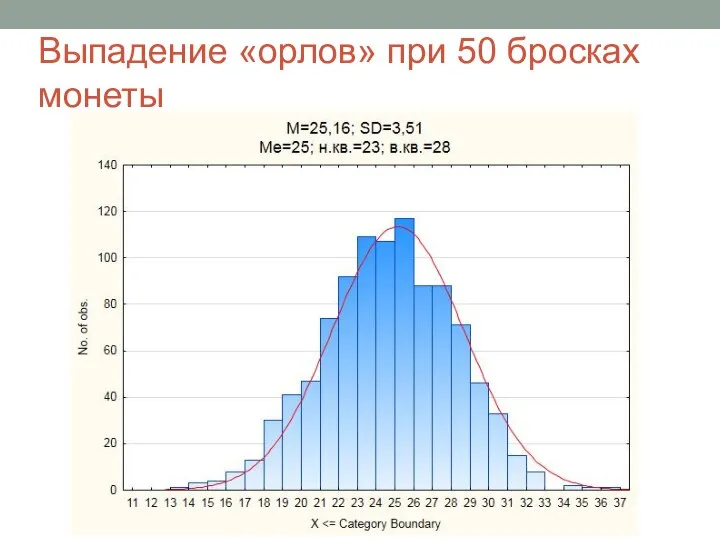
Выпадение «орлов» при 50 бросках монеты

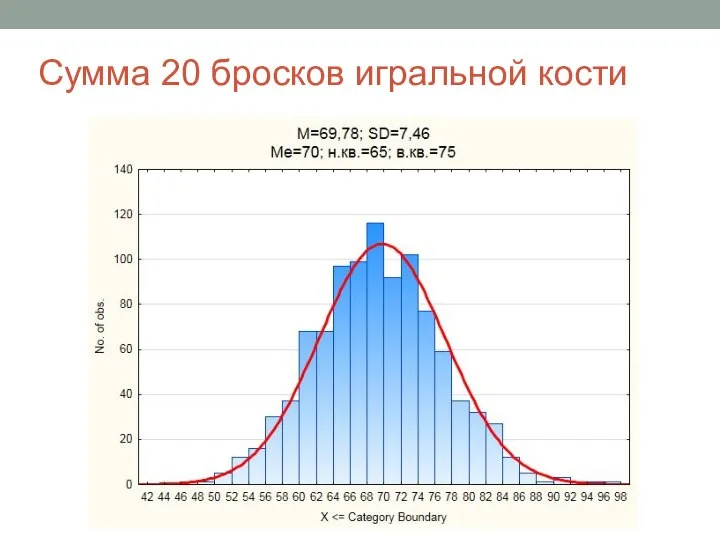
Сумма 20 бросков игральной кости

Свойство кривой
нормального распределения

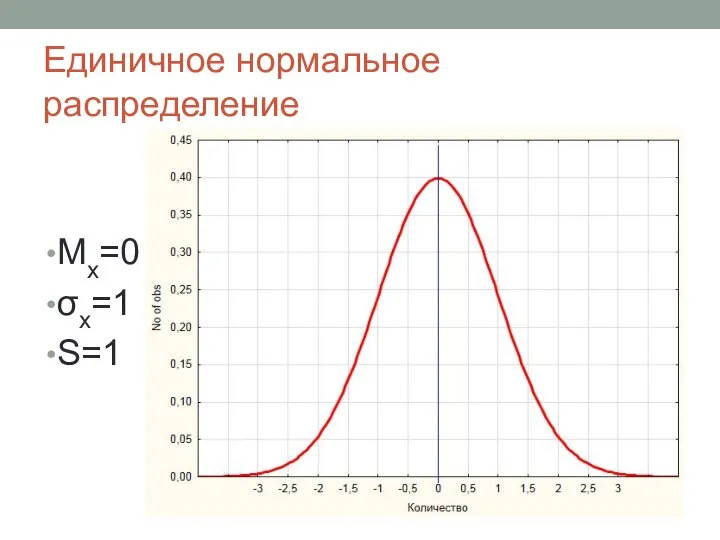
Единичное нормальное распределение
Мх=0
σх=1
S=1

Формулы перехода между шкалами

Возможные причины отклонения
от нормальности распределения
Наличие большого количества выбросов;
Погрешность измерения (шкала перестала быть метрической);
NB! Если шкала перестала быть метрической, она все равно остается количественной – а именно, ранговой, так как по-прежнему обладает всеми ее свойствами.
Влияние неучтенной (побочной) переменной.

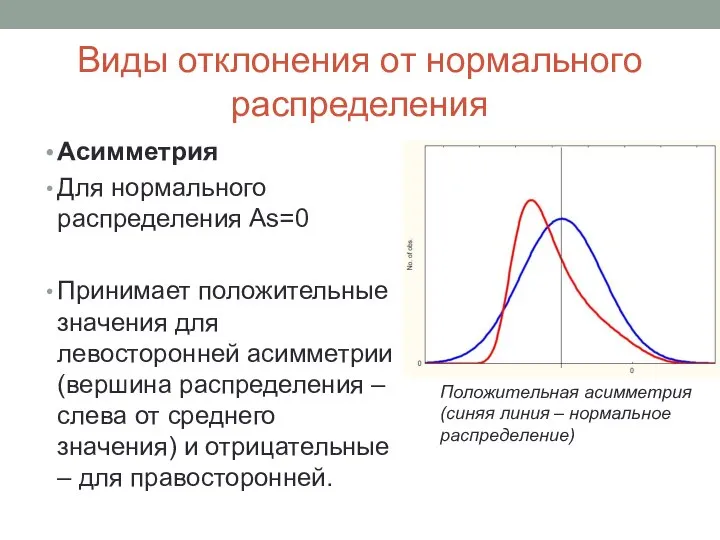
Виды отклонения от нормального распределения
Асимметрия
Для нормального распределения As=0
Принимает положительные значения для левосторонней асимметрии (вершина распределения – слева от среднего значения) и отрицательные – для правосторонней.
Положительная асимметрия
(синяя линия – нормальное распределение)

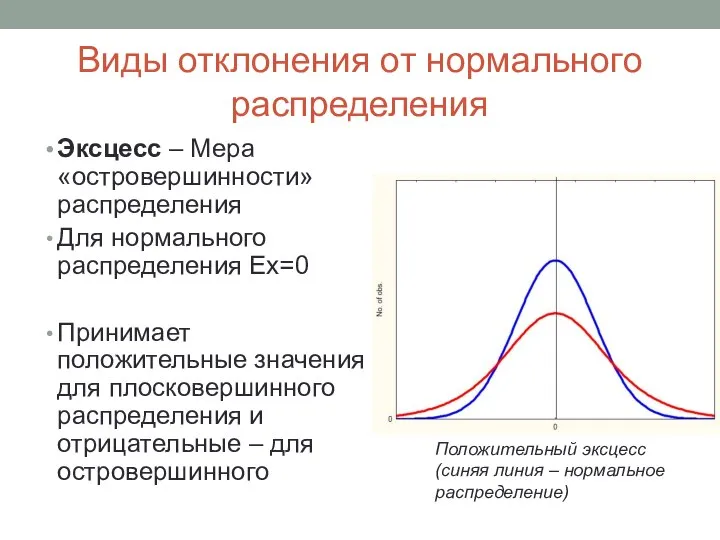
Виды отклонения от нормального распределения
Эксцесс – Мера «островершинности» распределения
Для нормального распределения Ex=0
Принимает
положительные значения для плосковершинного распределения и отрицательные – для островершинного
Положительный эксцесс
(синяя линия – нормальное распределение)

Шкала стенов
Стены (STAndart Ten) – «стандартная десятка». Шкала состоит из 10 возможных целых значений (от 1 до 10), для которой Мх=5,5 и σх=2.
Дробные значения округляются до целых.
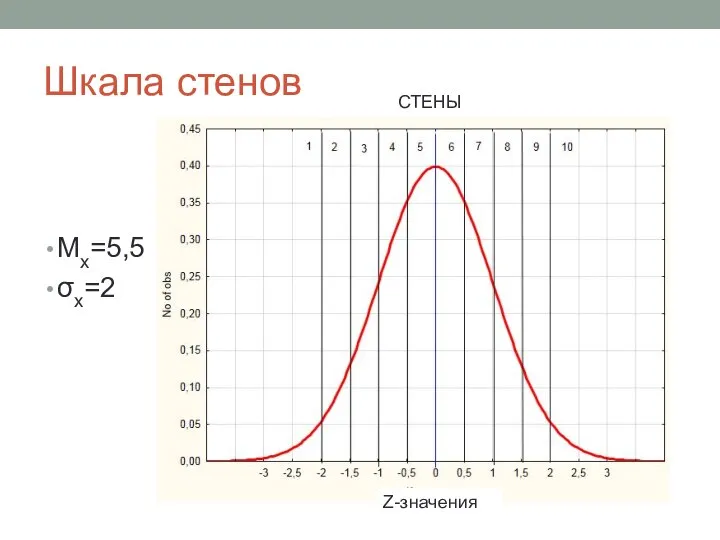
Пользуясь формулами перехода между шкалами, любой признак, имеющий примерно нормальное распределение, можно выразить в стенах.

Шкала стенов
Мх=5,5
σх=2
СТЕНЫ
Z-значения

Другие стандартные тестовые шкалы
Шкала Векслера (шкала IQ):
Мх=100
σх=15
Шкала Т-баллов:
Мх=50
σх=10

Стандартная ошибка среднего

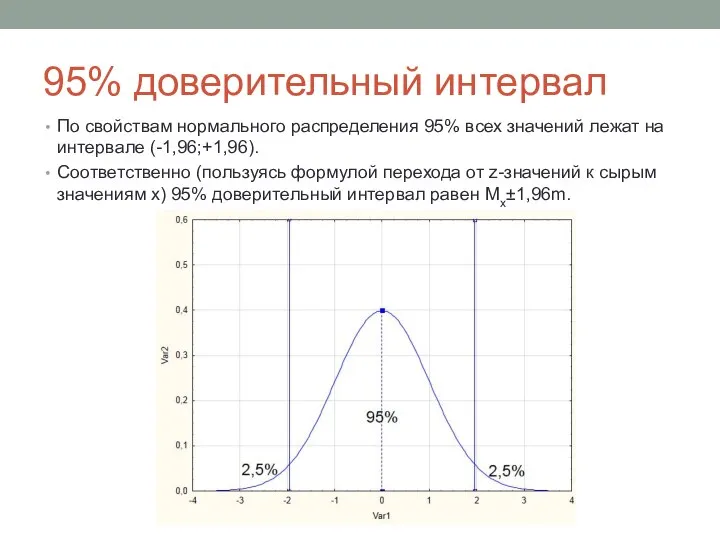
95% доверительный интервал
По свойствам нормального распределения 95% всех значений лежат на интервале (-1,96;+1,96).
Соответственно (пользуясь формулой перехода от z-значений к сырым значениям х) 95% доверительный интервал равен Мх±1,96m.

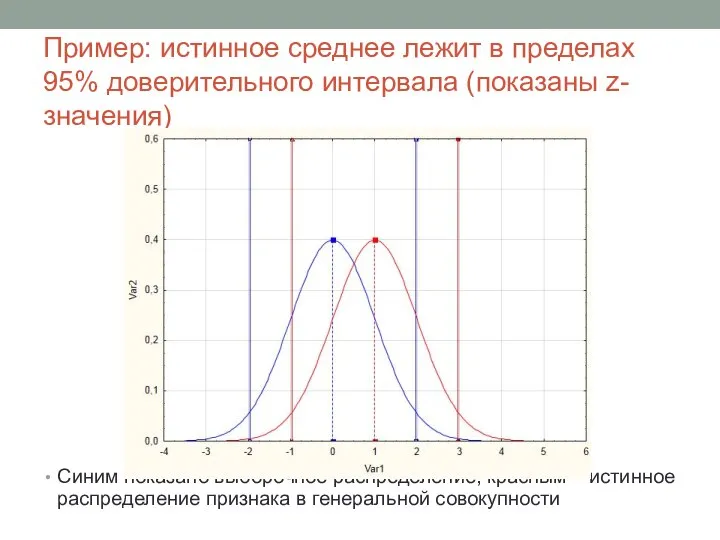
Пример: истинное среднее лежит в пределах 95% доверительного интервала (показаны z-значения)
Синим показано выборочное распределение, красным – истинное распределение признака в генеральной совокупности

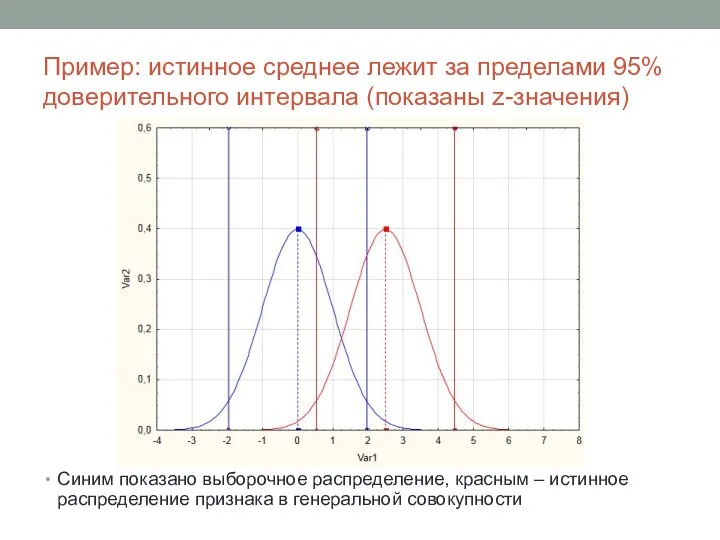
Пример: истинное среднее лежит за пределами 95% доверительного интервала (показаны z-значения)
Синим показано выборочное распределение, красным – истинное распределение признака в генеральной совокупности

Наиболее распространенные доверительные интервалы
95% доверительный интервал равен Мх±1,96m.
99% доверительный интервал примерно соответствует Мх±2,58m (точнее, Мх±2,575m).
90% доверительный интервал примерно соответствует Мх±1,64m.