Содержание
- 2. Кодирование и декодирование Для обмена информацией с другими людьми человек использует естественные языки. Наряду с естественными
- 3. Способы кодирования информации Для кодирования одной и той же информации могут быть использованы разные способы; их
- 4. Способы кодирования информации Выбор способа кодирования информации может быть связан с предполагаемым способом ее обработки. Покажем
- 5. Шифрование сообщения В некоторых случаях возникает потребность засекречивания текста сообщения или документа, для того чтобы его
- 6. Первый телеграф Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в1837 году американцем Сэмюэлем
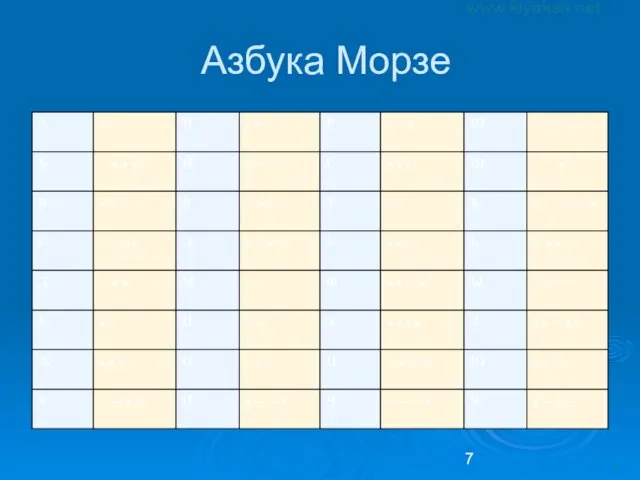
- 7. Азбука Морзе
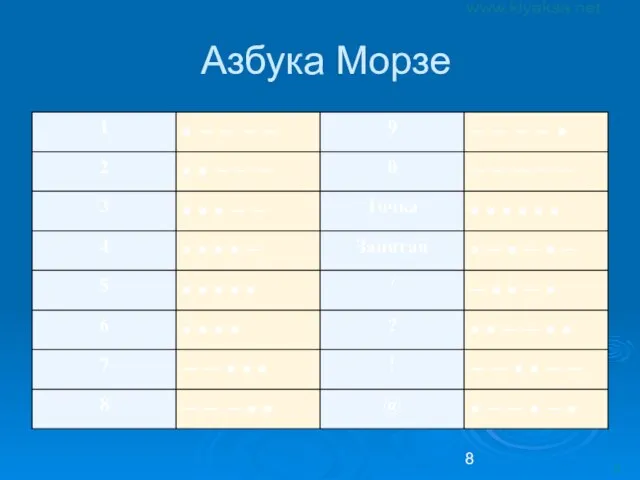
- 8. Азбука Морзе
- 9. Неравномерность кода − • − − • • • − − • • − Характерной особенностью
- 10. Первый беспроводной телеграф (радиоприемник) 7 мая 1895 года российский ученый Александр Степанович Попов на заседании Русского
- 11. Телеграфный аппарат Бодо Равномерный телеграфный код был изобретен французом Жаном Морисом Бодо в конце XIX века.
- 12. Двоичное кодирование в компьютере Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью
- 13. Почему двоичное кодирование С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось
- 14. Двоичное кодирование текстовой информации Начиная с 60-х годов, компьютеры все больше стали использовать для обработки текстовой
- 15. 1 символ – 1 байт (8 бит) Для кодирования одного символа требуется один байт информации. Учитывая,
- 16. Двоичное кодирование текстовой информации Кодирование заключается в том, что каждому символу ставиться в соответствие уникальный двоичный
- 17. Таблица кодировки Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера (коды), называется
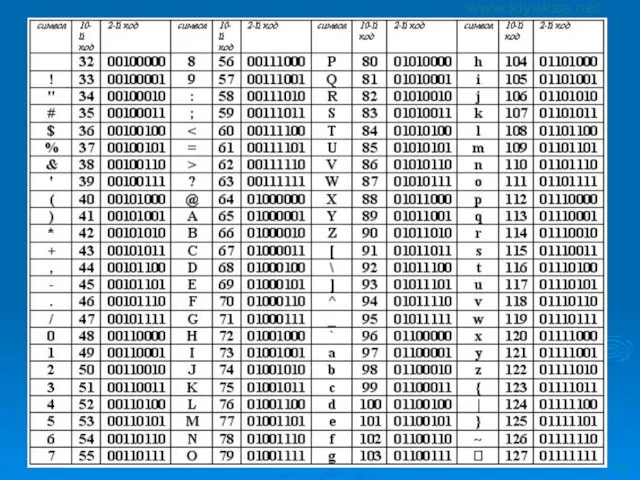
- 18. Таблица кодировки ASCII Стандартной в этой таблице является только первая половина, т.е. символы с номерами от
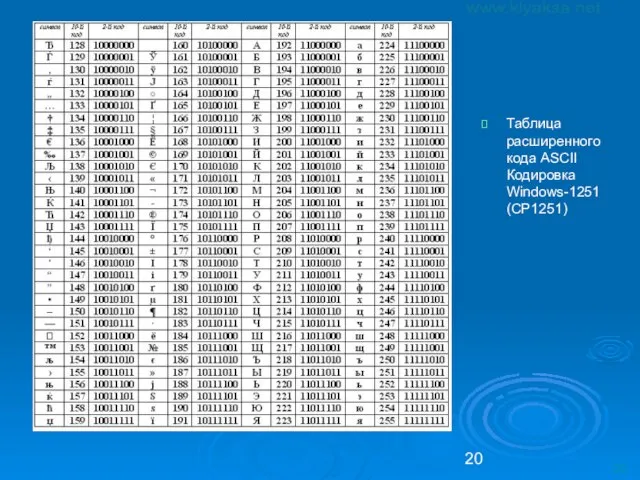
- 20. Таблица расширенного кода ASCII Кодировка Windows-1251 (CP1251)
- 21. Обратите внимание! Цифры кодируются по стандарту ASCII в двух случаях – при вводе-выводе и когда они
- 22. Система счисления Для записи информации о количестве объектов используются числа. Числа записываются с помощью набора специальных
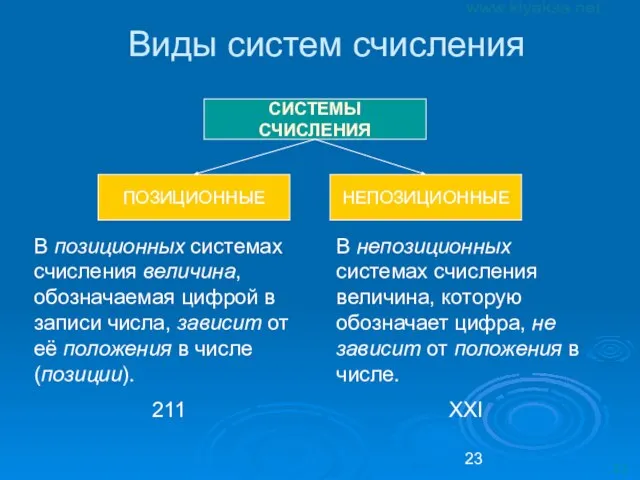
- 23. Виды систем счисления СИСТЕМЫ СЧИСЛЕНИЯ ПОЗИЦИОННЫЕ НЕПОЗИЦИОННЫЕ В непозиционных системах счисления величина, которую обозначает цифра, не
- 24. Непозиционные системы счисления Каноническим примером фактически непозиционной системы счисления является римская, в которой в качестве цифр
- 25. Задание: XIX= MMMD= MCMXCIVII= XXII-V= LXVI:XI= XXIV*VII= 3500 19 1996 17 6 168 CLXVIII
- 26. Позиционные системы счисления В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её
- 27. Развернутой формой числа называется запись: Aq=+-(an-1*qn-1+an-2*qn-2+…+a0*q0+a-1*q-1+ …+a-m*q-m), где А – само число, q-основание, а – цифры
- 28. Первые позиционные системы счисления Самой первой такой системой, когда счетным "прибором" служили пальцы рук, была пятеричная.
- 29. Двенадцатеричная система счисления Следующей после пятеричной возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Некоторые
- 30. Шестидесятеричная система счисления Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация
- 31. Какие позиционные системы счисления используются сейчас? В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная
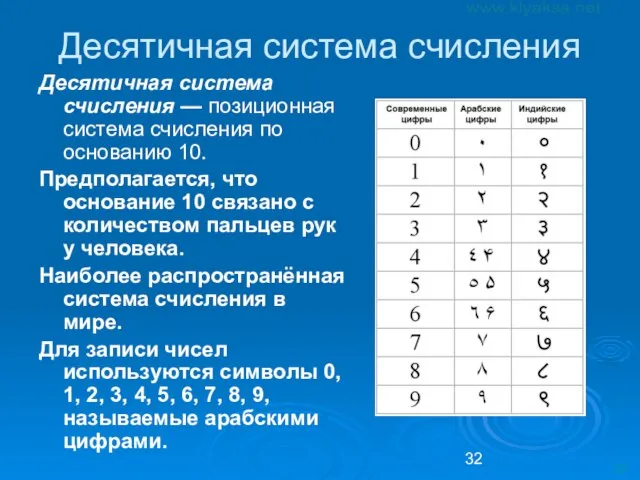
- 32. Десятичная система счисления Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание
- 33. Двоичная система счисления Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0
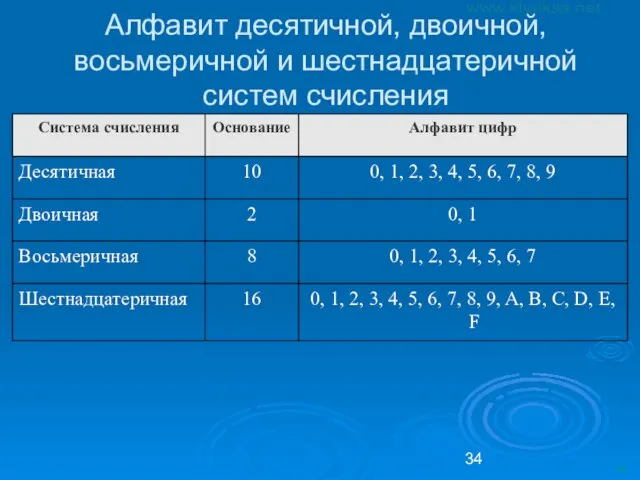
- 34. Алфавит десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
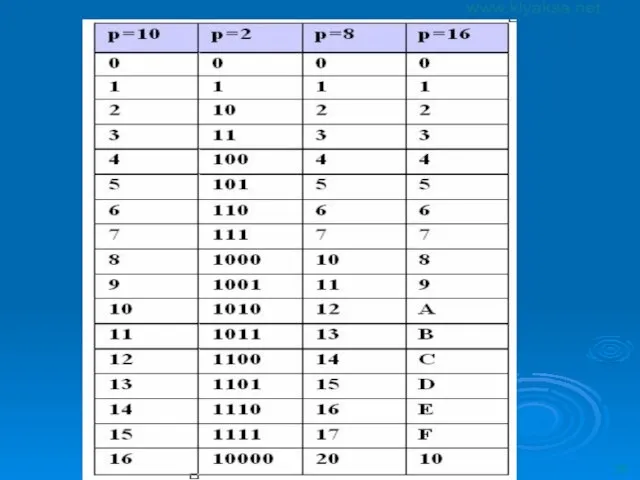
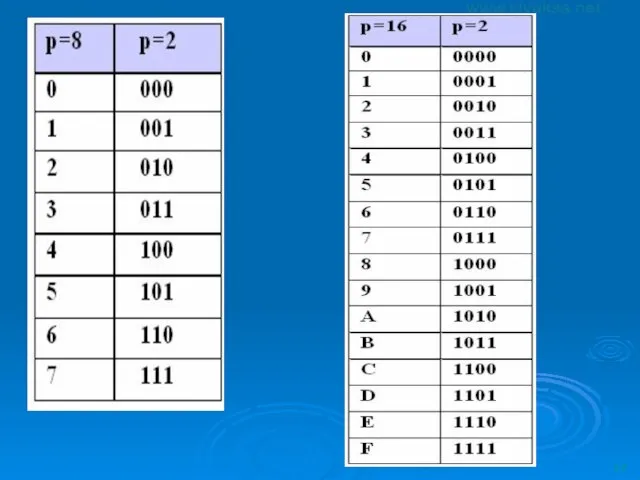
- 35. Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления Количество используемых цифр называется основанием системы счисления и
- 37. Перевод чисел из одной системы счисления в другую Чтобы перевести число из позиционной системы счисления с
- 38. Перевод чисел из одной системы счисления в другую Перевод из десятичной системы счисления в систему счисления
- 39. Перевод десятичных чисел. Перевести дробную часть в десятичную систему счисления и последовательно её умножать на основу
- 40. ? Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления. Ответ:
- 41. ? Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления. Ответ:
- 42. ? Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления. Ответ:
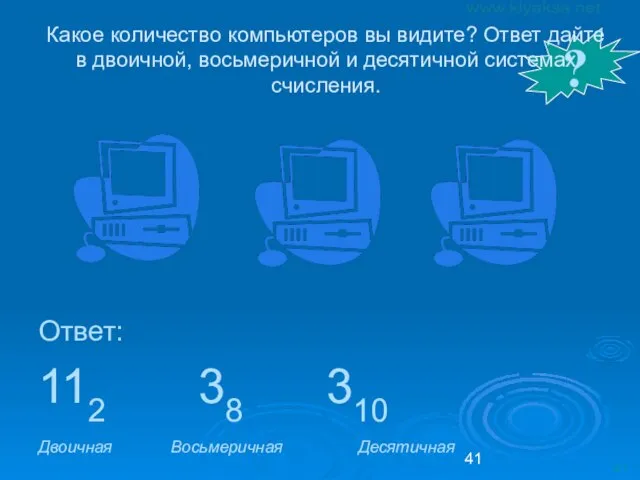
- 43. ? Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления. Ответ:
- 44. ? Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления. Ответ:
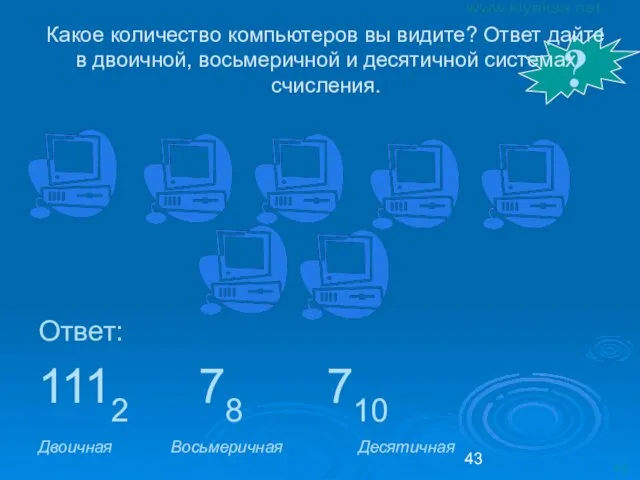
- 45. ? Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления. Ответ:
- 46. Числа в компьютере Числа в компьютере хранятся и обрабатываются в двоичной системе счисления. Последовательность нулей и
- 48. Задания: Прочитайте стихотворение. Переведите встречающиеся в нем числительные из двоичной системы счисления в десятичную. Необыкновенная девчонка
- 49. Вопросы: У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001
- 51. Скачать презентацию





































 Происхождение русского алфавита
Происхождение русского алфавита Урок презентация И.А. Крылов Зеркало и Обезьяна
Урок презентация И.А. Крылов Зеркало и Обезьяна Вариант
Вариант Половое размножение
Половое размножение Sega Retro Mania
Sega Retro Mania Предпринимательская деятельность гражданина
Предпринимательская деятельность гражданина Вопросы современного качества дошкольного образования
Вопросы современного качества дошкольного образования Non conform part N°1. Bonding issue
Non conform part N°1. Bonding issue Сражения Отечественной войны.
Сражения Отечественной войны. Презентация на тему Откуда берётся и куда девается мусор
Презентация на тему Откуда берётся и куда девается мусор  Анализ и совершенствование системы управления персоналом как средство повышения конкурентоспособности организации
Анализ и совершенствование системы управления персоналом как средство повышения конкурентоспособности организации Ch1-LinEquations (1)
Ch1-LinEquations (1) Об особенностях подготовки и проведения государственной итоговой аттестации в 2016 году
Об особенностях подготовки и проведения государственной итоговой аттестации в 2016 году Презентация на тему Глухие и звонкие парные согласные в корне слова
Презентация на тему Глухие и звонкие парные согласные в корне слова Education
Education  Экономика игровых механик для игр в социальных сетях
Экономика игровых механик для игр в социальных сетях Абдулла Алиш
Абдулла Алиш Загрязнение гидросферы
Загрязнение гидросферы Организация образовательного пространства начальной школы и развитие учительского потенциала при переходе на НСОТ
Организация образовательного пространства начальной школы и развитие учительского потенциала при переходе на НСОТ Требования к текстам документов, изготовляемых с помощью технических средств
Требования к текстам документов, изготовляемых с помощью технических средств Нормативно-правовое и технологическое обеспечение проведения государственной итоговОй аттестации в 2011-2012 учебном году
Нормативно-правовое и технологическое обеспечение проведения государственной итоговОй аттестации в 2011-2012 учебном году Титаны эпохи Возрождения
Титаны эпохи Возрождения Возможности сетевого взаимодействия в профессиональном росте педагога
Возможности сетевого взаимодействия в профессиональном росте педагога Правила съемки воды
Правила съемки воды Современные методы лечения острой кровопотери
Современные методы лечения острой кровопотери  Презентация Идеи для календаря
Презентация Идеи для календаря МАРКЕТИНГ ИННОВАЦИЙ
МАРКЕТИНГ ИННОВАЦИЙ Паркеты. Правильные, полуправильные
Паркеты. Правильные, полуправильные