Содержание
- 2. Комбинаторика
- 3. КОМБИНАТОРИКА- раздел математики, в котором изучаются простейшие «соединения», которые можно составить из n предметов, меняя всеми
- 4. Способ схем
- 5. Задача №1 Ужасные грабители Кнопка и Скрепка решили украсть из сейфа золотой ключик Буратино. Для того
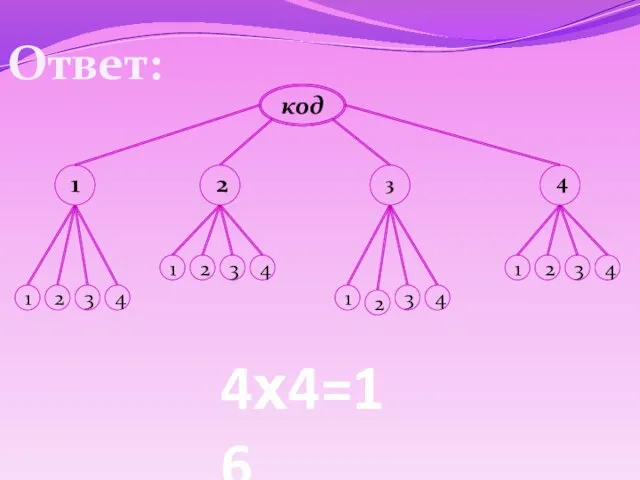
- 6. Ответ: код 1 2 3 4 1 2 3 4 1 2 3 4 1 2
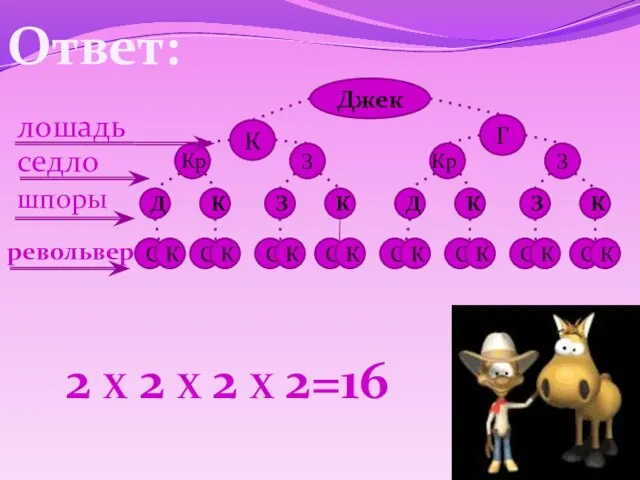
- 7. Задача № 2 У ковбоя Джека две лошади: каурой и гнедой масти, два седла: красное и
- 8. Ответ: Джек К З Д К З К Кр С К С К С К С
- 9. Задача №3 В распоряжении имеется 5 флажков: синий, белый, красный, оранжевый, зелёный. Для передачи некоторого сообщения
- 10. Ответ: 1 способ 2 способ 3 способ 4 способ 5 х 4 х 3=60
- 11. Задача №4 В школьном драмкружке решили ставить гоголевского «Ревизора». И тут начался спор. Всё началось с
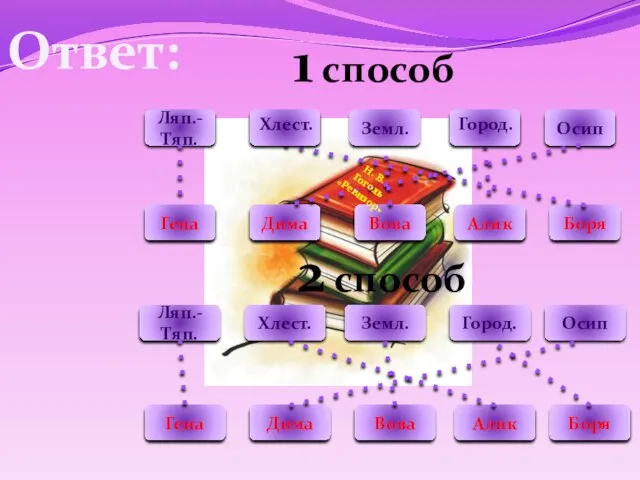
- 12. Ответ: Ляп.-Тяп. Земл. Осип Гена Дима Алик Боря Вова 1 способ 2 способ Ляп.-Тяп. Хлест. Земл.
- 13. Способ умножения
- 14. Задача №1 Решение: У двадцати обезьян 20 х 4 = 80 лап и 20 х 4
- 15. Сколькими способами Кролик может рассадить пять гостей на пяти разноцветных табуретках? Задача №2 Решение: Двух гостей
- 16. В некотором городе у всех велосипедистов были трехзначные номера. Но велосипедисты попросили, чтобы в этих номерах
- 17. Задача №4 К Маше пришли три гостя: Саша, Паша и Даша. Сколькими способами она может рассадить
- 19. Скачать презентацию













 Организация и проведение мероприятий направленных на привлечение детей занятиями лыжным спортом
Организация и проведение мероприятий направленных на привлечение детей занятиями лыжным спортом Елочные игрушки
Елочные игрушки «О совершенствовании государственной политики в области технического регулирования в целях модернизации и технологического раз
«О совершенствовании государственной политики в области технического регулирования в целях модернизации и технологического раз Презентация на тему Суждение как форма мышления
Презентация на тему Суждение как форма мышления Конденсаторы
Конденсаторы Интерактивный кроссворд для обучающихся 6 класса специальной (коррекционной) школы VIII вида «Словарные слова»
Интерактивный кроссворд для обучающихся 6 класса специальной (коррекционной) школы VIII вида «Словарные слова» Мотивація навчання в структурі розвитку особистості
Мотивація навчання в структурі розвитку особистості Обязанности судей перед игрой
Обязанности судей перед игрой Модульные технологии
Модульные технологии Оптимизация. Использование алгоритмов
Оптимизация. Использование алгоритмов Сколько стоит мусор?
Сколько стоит мусор? Презентация problem statement standard
Презентация problem statement standard Презентация на тему Декабристы. Первые русские революционеры (10 класс)
Презентация на тему Декабристы. Первые русские революционеры (10 класс) Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана А.В.Колчак-исследователь Арктики.
А.В.Колчак-исследователь Арктики. Взрывы
Взрывы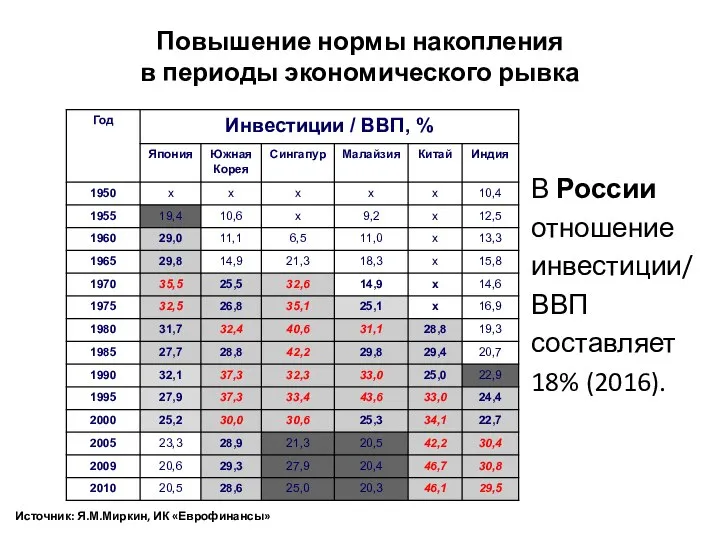 Повышение нормы накопления в периоды экономического рывка
Повышение нормы накопления в периоды экономического рывка Математика в музыке
Математика в музыке Презентация на тему Как написать сочинение
Презентация на тему Как написать сочинение Правильные и неправильные дроби
Правильные и неправильные дроби Новосибирск 2008
Новосибирск 2008 Использование технологии бюджетного управления для управления стоимостью и качеством внутренних услуг
Использование технологии бюджетного управления для управления стоимостью и качеством внутренних услуг Забавы по И. А. Крылову
Забавы по И. А. Крылову Сайт Ремонт.ру. Удобно. Практично. Надёжно
Сайт Ремонт.ру. Удобно. Практично. Надёжно Презентация на тему Логарифмы, логарифмическая функция
Презентация на тему Логарифмы, логарифмическая функция Перспективные направления развития современных технологий (10 класс)
Перспективные направления развития современных технологий (10 класс) Люблю природу русскую. Весна. Ф.И.Тютчев «Зима недаром злится»
Люблю природу русскую. Весна. Ф.И.Тютчев «Зима недаром злится» Презентация на тему ПОЛЕЗНАЯ АЗБУКА ПИТАНИЯ
Презентация на тему ПОЛЕЗНАЯ АЗБУКА ПИТАНИЯ