Содержание
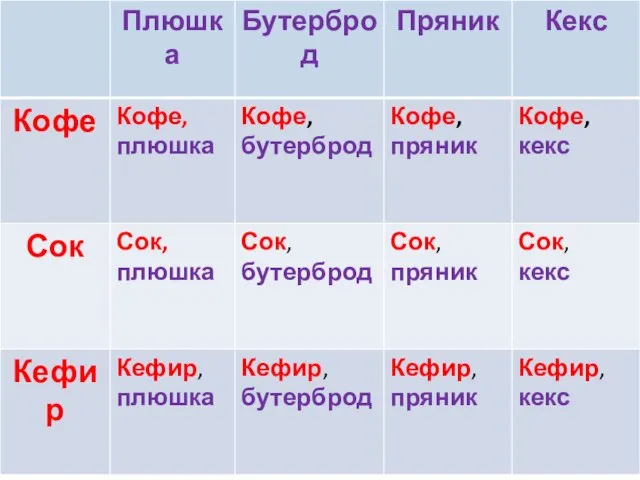
- 2. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе,
- 4. Правило умножения. Для того чтобы найти число всех возможных исходов независимого проведение двух испытаний А и
- 5. Пример 2. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных
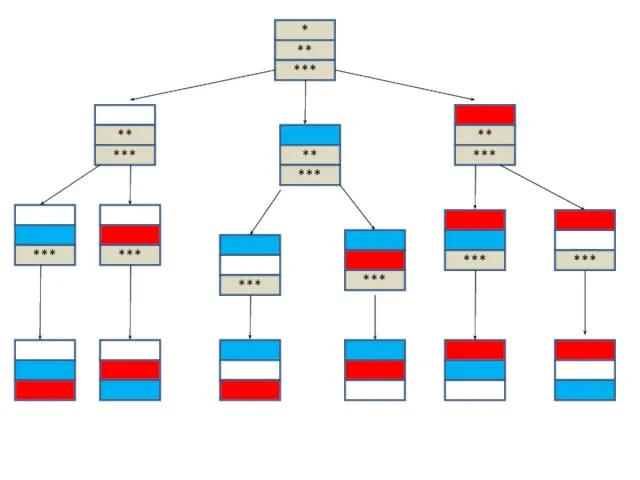
- 6. * ** *** * ** *** ** *** ** *** * *** * *** * ***
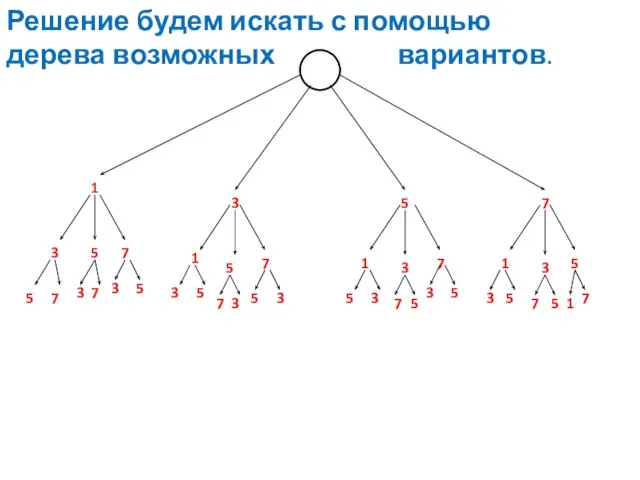
- 7. Сколько трехзначных чисел можно составить из цифр 1,3,5 и 7, используя в записи числа каждую из
- 8. Решение будем искать с помощью дерева возможных вариантов. 1 3 5 7 3 5 7 1
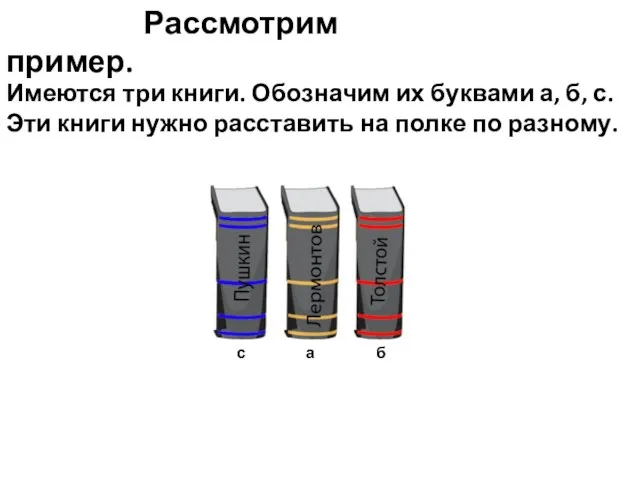
- 9. Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на
- 10. а с б
- 11. б а с
- 12. Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на
- 13. Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на
- 14. Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на
- 15. Перестановкой из n элементов называют каждое расположения этих элементов в определенном порядке. Обозначают Pn = n!
- 16. Задача №1 Сколькими способами 4 человека смогут разместиться на четырехместной скамейке?
- 17. Задача №2 Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из чисел 0,2,4,6?
- 18. Задача №3 Имеются девять различных книг, четыре из которых учебники. Сколькими способами можно расставить эти книги
- 19. Задача № 4 В расписании на понедельник шесть уроков : алгебра, геометрия, биология, история, физкультура, химия.
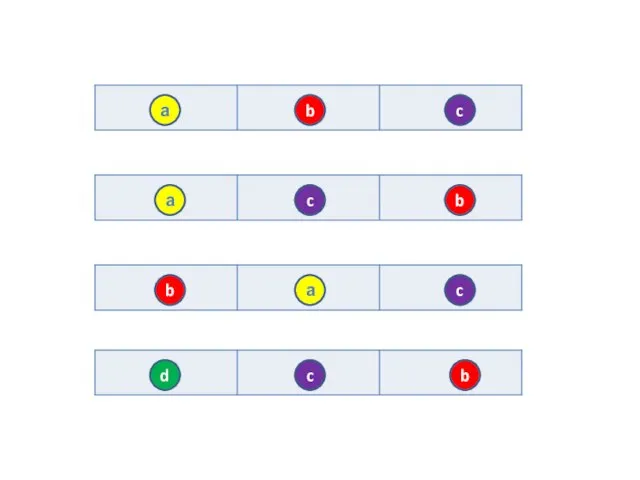
- 20. Пусть имеются 4 шара и 3 пустых ячейки. Обозначили шары буквами a, b, c, d. В
- 21. а b c а c b b а c c b d
- 22. abc, abd, acb, acd, adb, adc, bac, bad, bca, bcd, bda, bdc cab, cad, cba, cbd,
- 23. Размещением из n элементов по k (k в определенном порядке из данных n элементов. A
- 24. A = n*(n-1)(n-2)…(n-(k-1))
- 25. Ann =Pn=n!
- 26. Задача № 5 Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один
- 27. Задача №6 На странице альбома 6 свободных мест для фотографий. Сколько существует способов размещения фотографий в
- 28. Задача №7 Сколько трехзначных чисел ( без повторения цифр в записи числа) можно составить из цифр
- 29. Решение А73-А62= 7*6*5-6*5=6*5(7-1)=6*5*6=180
- 30. Задача №8 Из трехзначных чисел, записанных с помощью цифр 1, 2, 3, 4,5, 6, 7, 8,
- 31. Задача №9 Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отличается
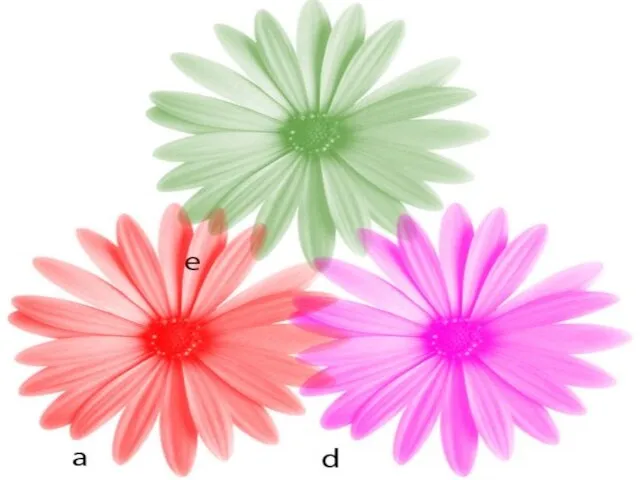
- 39. Если в букет не входит цветок а, а входит b, то можно получить такие букеты:
- 44. Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных
- 45. Cnk=
- 46. Задача № 10 Из 15-ти членов туристической группу надо выбрать трех дежурных. Сколькими способами можно сделать
- 47. Задача №11 Из вазы с фруктами, где лежит 9 яблок и 6 груш, нужно выбрать 3
- 48. Задачи для закрепления
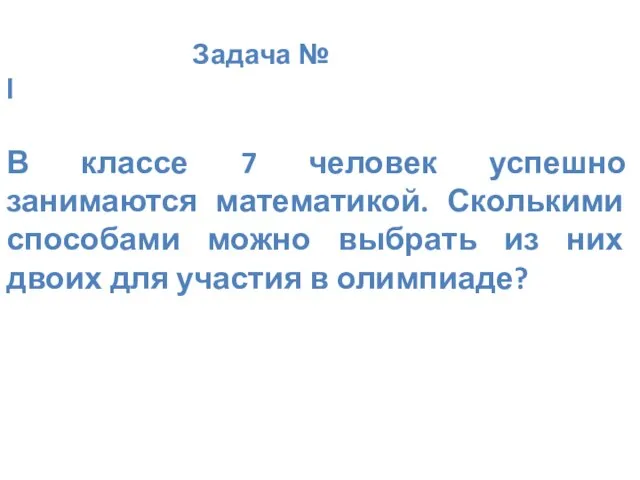
- 49. Задача № I В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них
- 50. Задача № II В лаборатории, в которой работают заведующий и 10 сотрудников, надо отправить в командировку
- 51. Задача № III В классе учатся 16 мальчиков и 12 девочек. Для уборки территории нужно выделить
- 53. Скачать презентацию

















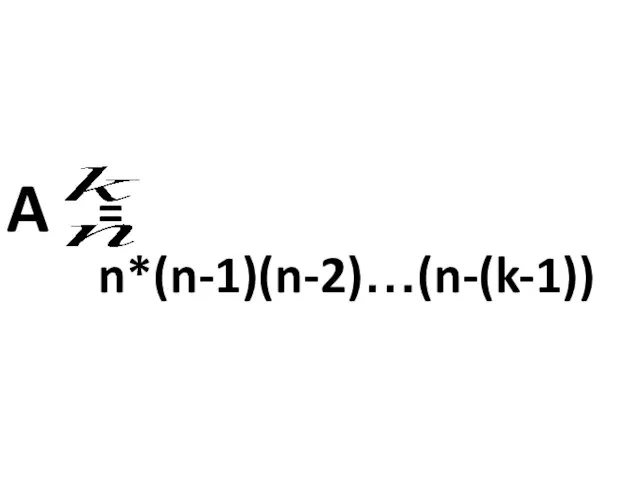
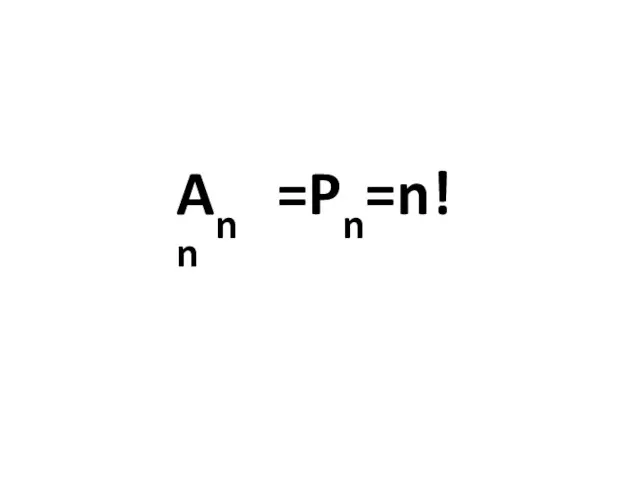


















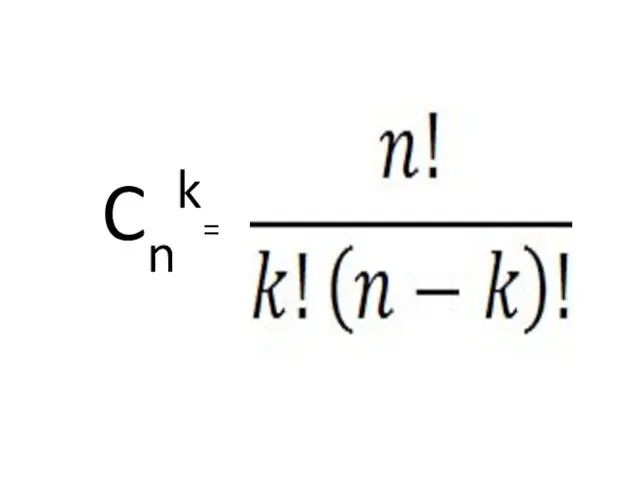





 Стандарты и спецификации в области информационной безопасности
Стандарты и спецификации в области информационной безопасности Получение разрешения на осуществление деятельности по проведению независимой идентификационной экспертизы товаров
Получение разрешения на осуществление деятельности по проведению независимой идентификационной экспертизы товаров С днём рождения, Мамочка
С днём рождения, Мамочка Себестоимость. Формула
Себестоимость. Формула Презентация на тему Все профессии важны (2 класс)
Презентация на тему Все профессии важны (2 класс) Коммерческое предложение по реализации имущества, прав требований. ООО НПП ЗППС БИНАКА
Коммерческое предложение по реализации имущества, прав требований. ООО НПП ЗППС БИНАКА Подходы к менеджменту: системный, ситуационный, процессный
Подходы к менеджменту: системный, ситуационный, процессный ProSpace (Казахстан)
ProSpace (Казахстан) Технология создания gif-анимации в Photoshop или ImageReady
Технология создания gif-анимации в Photoshop или ImageReady Эмпатическое слушание
Эмпатическое слушание vydacha_zadaniy (1) (1)
vydacha_zadaniy (1) (1) Отделка - это завершающая операция при изготовлении изделий
Отделка - это завершающая операция при изготовлении изделий Правотворческая деятельность на муниципальном уровне:
Правотворческая деятельность на муниципальном уровне: Пастернак Борис Леонидович ( 1890 - 1960 )
Пастернак Борис Леонидович ( 1890 - 1960 ) Презентация на тему СИЛА ТРЕНИЯ ПОКОЯ Силы в механике
Презентация на тему СИЛА ТРЕНИЯ ПОКОЯ Силы в механике  Dr.Web Enterprise Suite
Dr.Web Enterprise Suite Социальный контекст инновационного развития
Социальный контекст инновационного развития РМО учителей биологии и экологии
РМО учителей биологии и экологии Differences_between_British_and_American_versions_of_English_2 (2)
Differences_between_British_and_American_versions_of_English_2 (2) Диверсификация профессиональных навыков разработчикаДмитрий Васильев
Диверсификация профессиональных навыков разработчикаДмитрий Васильев Урок технологии
Урок технологии Практика построения системы управления техническим обслуживанием и ремонтами оборудования (ТОиР)(Использование программных инс
Практика построения системы управления техническим обслуживанием и ремонтами оборудования (ТОиР)(Использование программных инс Грузинский Технический Университет. Тбилиси
Грузинский Технический Университет. Тбилиси Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Итоги Декады качества предоставления государственных услуг в сфере социальной поддержки и социального обслуживания населения
Итоги Декады качества предоставления государственных услуг в сфере социальной поддержки и социального обслуживания населения Клітинкові автомати
Клітинкові автомати Универсальная система учёта и паспортизации
Универсальная система учёта и паспортизации Мижоз хар доим хақ, энг ачинарлиси у бу хақида билади
Мижоз хар доим хақ, энг ачинарлиси у бу хақида билади