Комбинаторные задачи (7 класс)

Цель: составить сборник задач по данной теме.
Задачи:
рассмотреть примеры комбинаторных задач
научиться выделять основные типы задач
рассмотреть алгоритмы и схемы для решения задач
составить аналогичные задачи
представить результат своей деятельности, в виде сборника задач

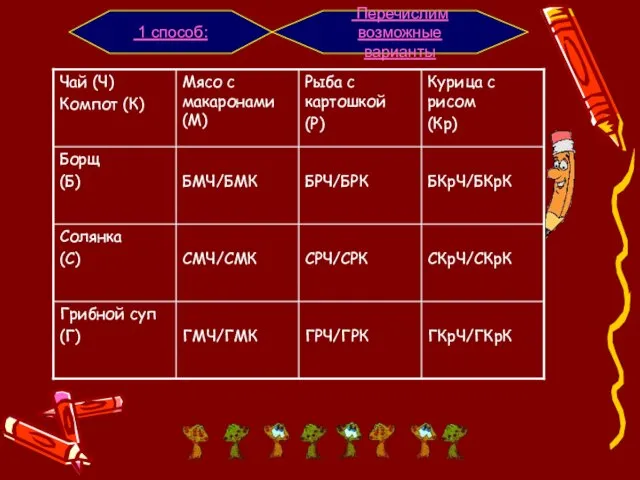
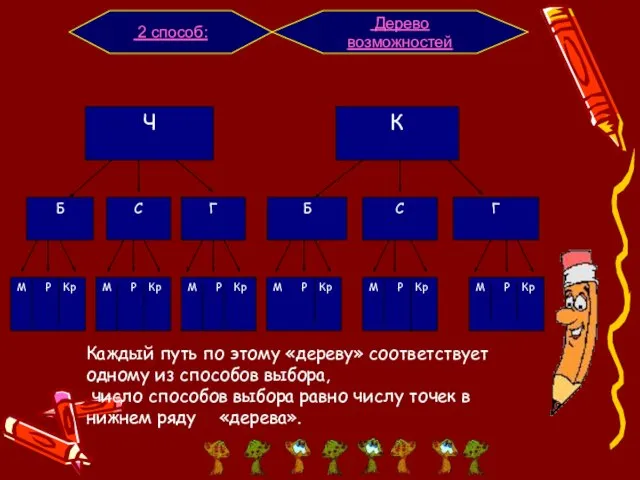
Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей.
Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий, но которые нельзя описать или охарактеризовать с помощью неизменных закономерностей в виде формул, правил, теорем и т.п.
Навыки решения задач используются, как в часы досуга, так и для работы в секретных службах, развития математических способностей. Мы полагаем, что результаты нашей работы вызовут интерес у учащихся и ребят, интересующихся математикой. Поэтому наш сборник можно использовать на уроках, как дидактический материал по теме «Решение задач на перестановки, размещения и сочетания» и упражнения для развития логики и внимания, в виде занимательных квадратов.
Актуальность темы

Задача:
В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе – мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье – чай и компот. Сколько различных обедов можно составить из указанных блюд?
рассмотрим, например, “дерево возможностей”, которое
помогает решать разнообразные задачи,
касающиеся перебора вариантов
происходящих событий.

1 способ:
Перечислим возможные
варианты

Ч
К
Б
С
М Р Кр
Г
Б
С
Г
М Р Кр
М Р Кр
М Р Кр
М Р Кр
М Р Кр
2 способ:
Дерево возможностей
Каждый путь по этому «дереву» соответствует
одному из способов выбора,
число способов выбора равно числу точек в нижнем ряду «дерева».

Правило умножения заключается в том,
что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В,
т.е. в нашей задаче имеется 3 элемента:
первое, можно выбрать 3 раза,
второе – 3 раза и
третье – 2раза,
получаем: 3х3х2=18
3 способ
Правило умножения

В своей работе мы рассмотрели задачи на перестановки, сочетания и размещения.
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Число перестановок из n элементов обозначается символом Рn (Р из n элементов). Например.
Задача: в книжном шкафу на полке стоят 3 книги, эти книги можно переставить по разному:
Каждое из этих расположений называется перестановкой из трех элементов.
Таким образом Р3= 6.
Т.е. Р3= 3*2*1= 6 = 3!
Формула для вычислений: Рn =n!

Размещением из n элементов по k (k меньше или равно n) называется любое множество, состоящее из любых k элементов, взятых в определенном порядке из данных n элементов.
Обозначение: Ank ( читают: «А из n по k).
Задача:
Пусть имеется три шара и две пустых ячейки. В пустые ячейки можно разместить по два шара.
Решение: из трех элементов по два будут наборы (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
Размещения считаются различными, если они отличаются самими элементами или порядком их расположения. Например: (1,2), (2,1), (1,3), (3,1) в нашем примере.
В результате получаем: А32 = 3*2 = 6.
Задача:
Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
Решение: А84= 8*7*6*5 = 1680

Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов.
Обозначение: Cnk (читают С из n по k).
Задача: Пусть имеется три шара разного цвета. Нужно рассмотреть все возможные способы составления шаров, в которых сочетаются два цвета из данных трех.
Решение: из трех элементов (1;2;3) по два будут наборы (1,2),(1,3),(2,3).
В отличии от размещений в сочетаниях не имеет значение, в каком порядке указаны элементы. Два сочетания различны, если отличаются друг от друга хотя бы одним элементом. Например: (1,2),(1,3).
Решение: (2 способ).В нашем примере, в каждом сочетании выполнимы все перестановки. Число таких перестановок равно Р2. В результате получим все возможные комбинации из 3 элементов по 2, которые отличаются либо самими элементами, либо порядком элементов, т.е. все размещения из 3 элементов по 2. Всего мы получим А32 размещений. Значит если количество размещений разделить на количество перестановок, получим количество сочетаний из трех элементов по два. С32=А32/Р2=6:2=3.

Задача: Расположить натуральные числа
от 1 до 9 в магический квадрат 3х 3.
В магическом квадрате 3х 3 магической постоянной 15 должны быть равны сумме трех чисел по 8 направлениям: по 3 строкам, 3 столбцам и 2 диагоналям.
магические
и занимательные квадраты
Проведенное нами простое построение магического квадрата 3х 3 доказывает
его единственность.

"Сборник
задач".

Тема: «Метод перебора».
В школьной столовой было меню: из напитков - кофе, чай; гарнир – картошка, рис, перловка; мясное – курица, котлеты, тефтели. Сколько возможных вариантов обеда можно заказать в школьной столовой? (Архипова Юля 6Б класс)
Художнику надо было нарисовать картины о трех профессиях: продавец, повар и пожарник. Позировать для картины пришли два продавца Оля и Вера; три повара Андрей, Света и Ника; три пожарника – Леша, Миша и Паша. Сколько может получится картин у художника, ели в позировании примут участие все участники? (Искакова Айжан 6В класс)
В магазине продавали из хлебной продукции: кириешки, компашки, хлеб; из колбас – ливерную, докторскую, молочную; из напитков – сок, лимонад. Сколько покупок можно сделать из трех наименований? (Яковлев Константин 6В класс)

Тема: Перестановки, размещения, сочетания.
В спорт зале на полке находилось 7 футбольных мячей. Найти все возможные перестановки?
(Яковлев Константин 6В класс)
Учащиеся шестого класса изучают 12 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 6 различных предметов? (Яковлев Константин 6В класс)
В классе было 13 человек. Сколько возможных вариантов сесть за парты по одному? по два?
(Искакова Айжан 6В класс)
В классе 28 человек, надо выбрать на каждый день двух дежурных. Сколькими способами можно это сделать? (Ворошнина Ольга 6А класс)