Содержание
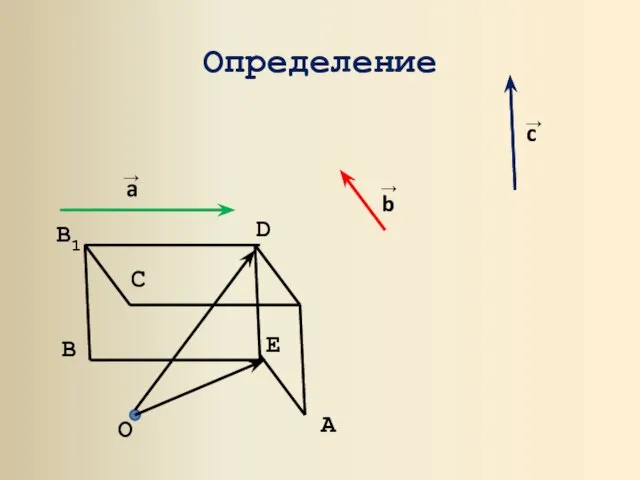
- 2. Определение Векторы называются компланарными, если при откладывании их от одной и той же точки они будут
- 3. Определение O A B B1 D C E
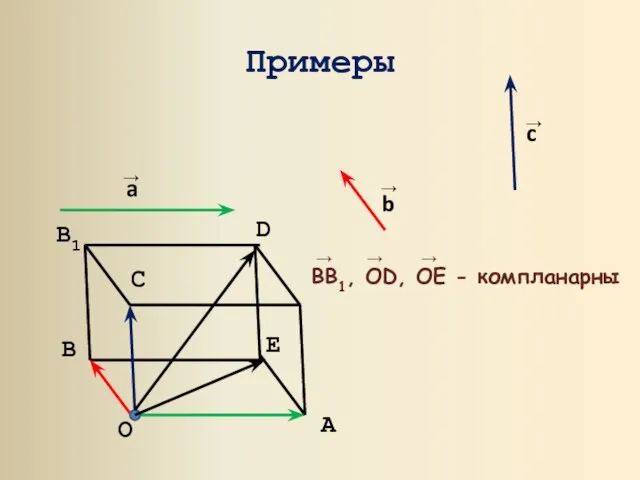
- 4. Примеры O A B B1 D C E
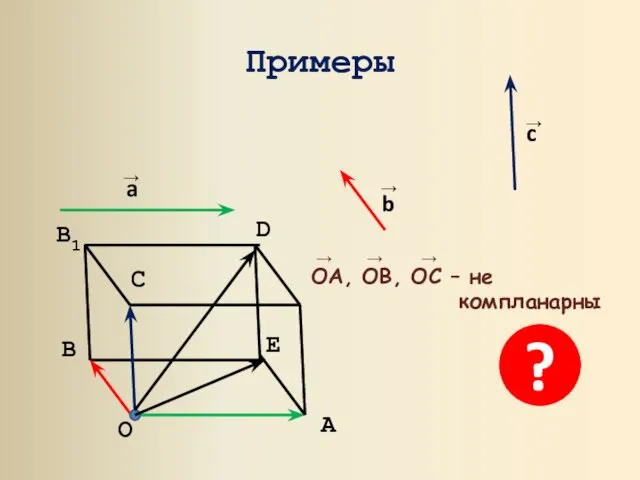
- 5. Примеры O A B B1 D C E ?
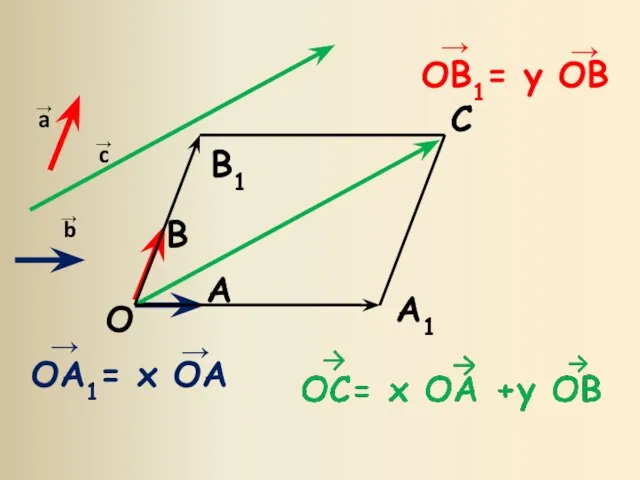
- 6. Если вектор с можно разложить по векторам a и b, т.е. представить в виде с= x
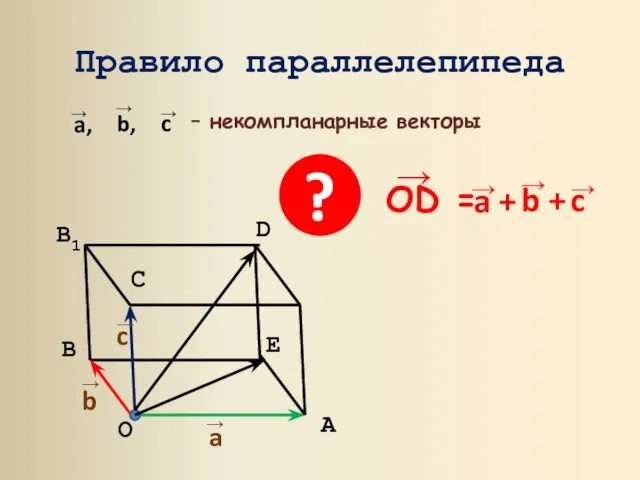
- 8. Правило параллелепипеда O A B B1 D C E ?
- 9. Разложение вектора по трем некомпланарным векторам Если вектор p представлен в виде p= x a +
- 10. Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
- 11. Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
- 13. Скачать презентацию





 Солнечная система
Солнечная система Германия. Школы будущего
Германия. Школы будущего My hobby hand made
My hobby hand made Презентация 4
Презентация 4 Духовная культура. Тест
Духовная культура. Тест «Плохие новости из белковой упаковки» Питер Медавар
«Плохие новости из белковой упаковки» Питер Медавар Умножение и деление ( закрепление)
Умножение и деление ( закрепление) Фотоотчёт по производственной практике
Фотоотчёт по производственной практике Человек в экономических отношениях 7 класс
Человек в экономических отношениях 7 класс Стандарт мерчандайзинга Места реализации «ЭЛЬБОР»
Стандарт мерчандайзинга Места реализации «ЭЛЬБОР» Животные тундры
Животные тундры Научно-практическая конференция «Теория развития: дифференционно-интеграционная парадигма» Москва, МГППУ, 24-25 февраля 2009 г. ОНТО
Научно-практическая конференция «Теория развития: дифференционно-интеграционная парадигма» Москва, МГППУ, 24-25 февраля 2009 г. ОНТО Измерение информационного объема сообщения
Измерение информационного объема сообщения Сальвадор Дали
Сальвадор Дали Парные согласные Б и П,звуки [б], [б’], [п], [п’].Строчная буква б.
Парные согласные Б и П,звуки [б], [б’], [п], [п’].Строчная буква б. День туриста (фотографии)
День туриста (фотографии) Золотая пропорция в архитектуре г.Лангепас
Золотая пропорция в архитектуре г.Лангепас Когда любовь в дефиците
Когда любовь в дефиците Биотические связи в природе
Биотические связи в природе Экономическое мышление
Экономическое мышление Презентация на тему Предложения с обращениями и вводными словами (8 класс)
Презентация на тему Предложения с обращениями и вводными словами (8 класс) Правописание гласных и согласных в корнях слов
Правописание гласных и согласных в корнях слов Управление человеческими ресурсами
Управление человеческими ресурсами Триединая цель урока
Триединая цель урока Петровские реформы и понятие моды
Петровские реформы и понятие моды Совушки
Совушки Первая медицинская помощь при травмах опорно-двигательного аппарата
Первая медицинская помощь при травмах опорно-двигательного аппарата Песня про царя Ивана Васильевича, молодого опричника и удалого купца Калашникова
Песня про царя Ивана Васильевича, молодого опричника и удалого купца Калашникова