ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ

Учитель математики
Маеренкова Вера Васильевна
ПОСТРОЕНИЕ
И ПРЕОБРАЗОВАНИЕ
ГРАФИКОВ
КВАДРАТИЧНОЙ
ФУНКЦИИ

Цели урока:
Образовательные:
экспериментальным путем получить алгоритмы построения графиков функций видов у=а(х-т)2, у=ах2+n, у=а(х-т)2+n , если известен график функции y=ах2;
научиться применять полученные алгоритмы к построению графиков функций.
Развивающие:
способствовать индивидуализации и дифференциации обучения с помощью применения информационно-коммуникационных технологий на уроках;
развивать у учащихся логическое мышление, внимание; формировать потребность в приобретении знаний
Воспитательные:
воспитывать навыки самоконтроля, привычки к рефлексии;
добиваться изменения роли ученика в учебном процессе от пассивного наблюдателя до активного исследователя.

Функция у =ах2, ее свойства и график
D(у)=R;
E(у)=[о;∞);
О(0;0) – вершина параболы;
Х=0 – ось симметрии
О
у
а>0
х
x
y

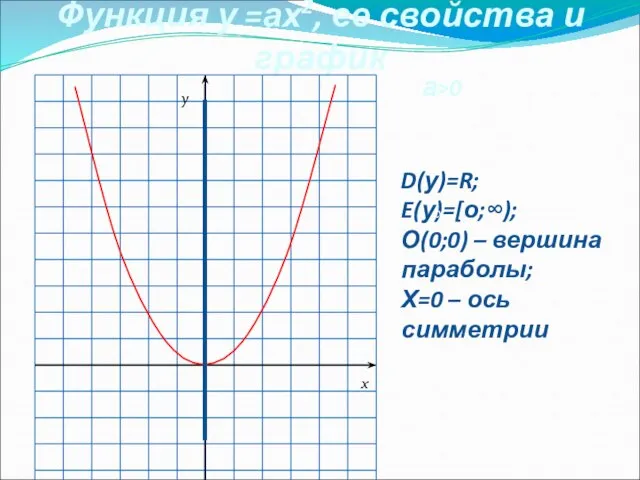
Функция у =ах2, ее свойства и график
а<0
D(у)=R;
E(у)=(-∞;0];
О(0;0) – вершина параболы;
х=0 – ось симметрии
x
y

Функция у =ах2+n, ее свойства
и график
Графиком функции у=ах2+n является парабола, которую можно получить из графика функции у =ах2 с помощью параллельного переноса вдоль оси у на n единиц вверх, если n>0, или на –n единиц вниз, если n<0

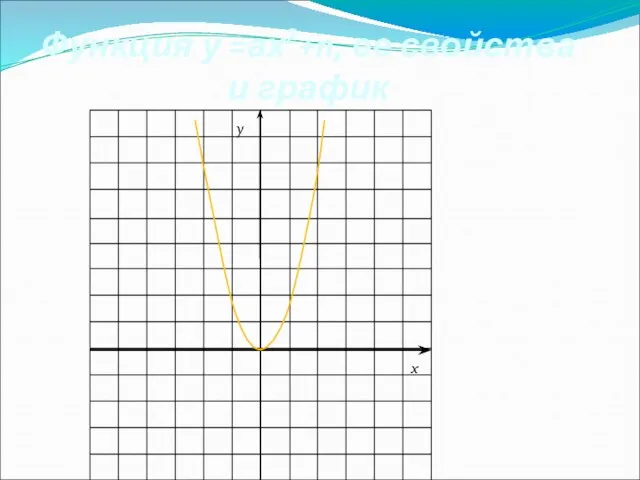
Функция у =ах2+n, ее свойства и график
x
y

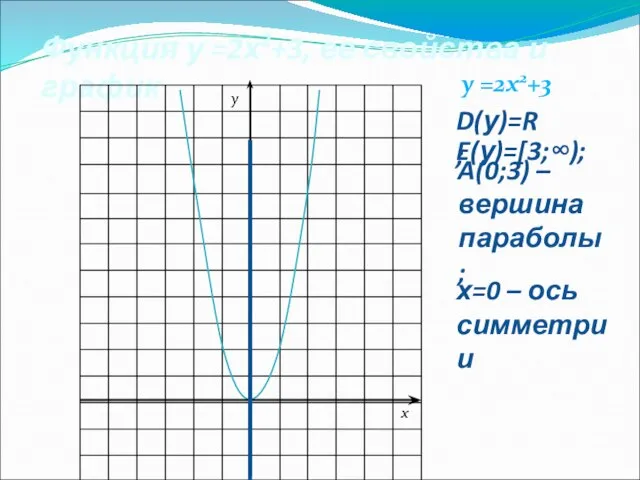
Функция у =2х2+3, ее свойства и график
A(0;3) –
вершина
параболы;
А
О
у
D(у)=R;
E(у)=[3;∞);
х=0 – ось
симметрии
у =2х2+3
x
y

Функция у =ах2+n, ее свойства и график
D(у)=R;
E(у)=(-∞; -3];
В(0;-3) – вершина параболы;
y=-¼x²-3
х=0 – ось
симметрии
x
y

Графиком функции у = а (х - т)2 является парабола, которую можно получить из графика функции у = ах2 с помощью параллельного переноса вдоль оси х на т единиц вправо, если т>0, или на –т единиц влево, если т<0

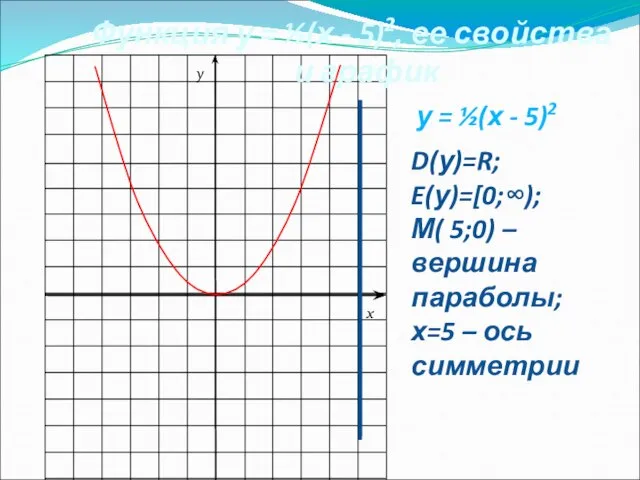
Функция у = ½(х - 5)2, ее свойства
и график
D(у)=R;
E(у)=[0;∞);
М( 5;0) – вершина параболы;
х=5 – ось
симметрии
у = ½(х - 5)2
x
y

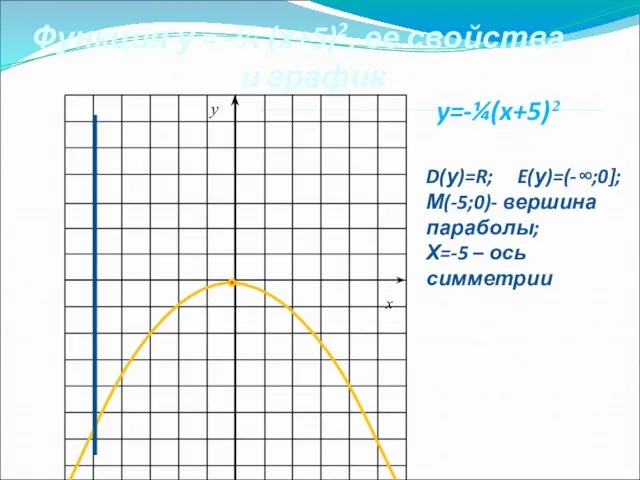
y
x
y=-¼(x+5)²
Функция у = -¼ (х+5)2, ее свойства
и график
D(у)=R; E(у)=(-∞;0];
М(-5;0)- вершина параболы;
Х=-5 – ось симметрии

Графиком функции у = а (х - т)2 + n является парабола, которую можно получить из графика функции у = ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на т единиц вправо, если т>0, или на – т единиц влево, если т<0, и сдвига вдоль оси у на n единиц вверх, если n >0, или на – n единиц вниз, если n <0

y=-¼(x+2)²+4
Функция у=-¼(х+2)2+4, ее свойства и график
D(у)=R;
E(у)=(-∞;4]; М(-2;4)- вершина
параболы;
х=-2 – ось симметрии
x
y

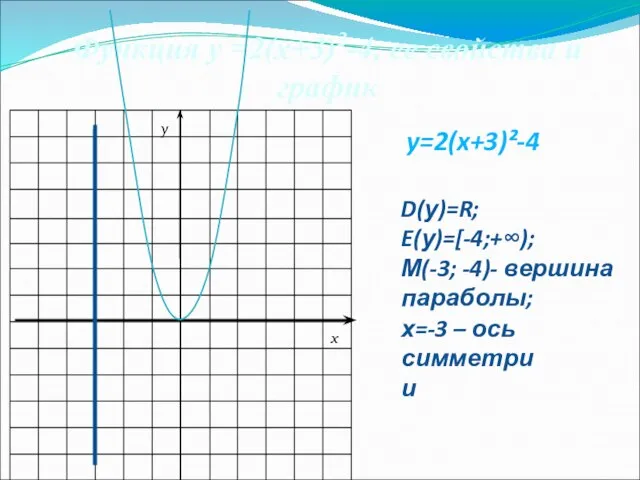
y=2(x+3)²-4
Функция у =2(х+3)2-4, ее свойства и график
D(у)=R;
E(у)=[-4;+∞); М(-3; -4)- вершина параболы;
х=-3 – ось
симметрии
x
y

Квадратичной функцией называется функция, которую можно задать формулой вида
у =ах2 + вх + с,
где х - независимая переменная,
а, в, и с -некоторые числа,
причем а ≠ 0.
Графиком функции является парабола

Графиком функции у=ах2+вх+с
является парабола, вершина которой есть точка (т; n), где
т=-b/2a
n = у(т)

Осью симметрии параболы служит прямая
х = т, параллельная оси у.
При а>0 ветви параболы направлены вверх, а при
а < 0 – вниз

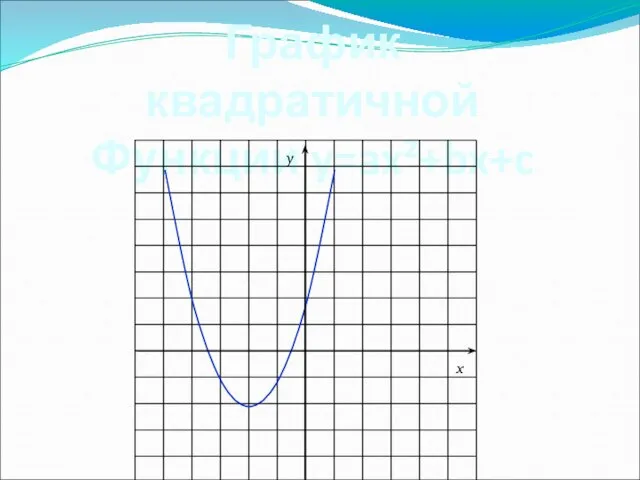
График квадратичной
Функции y=ax²+bx+c
x
y

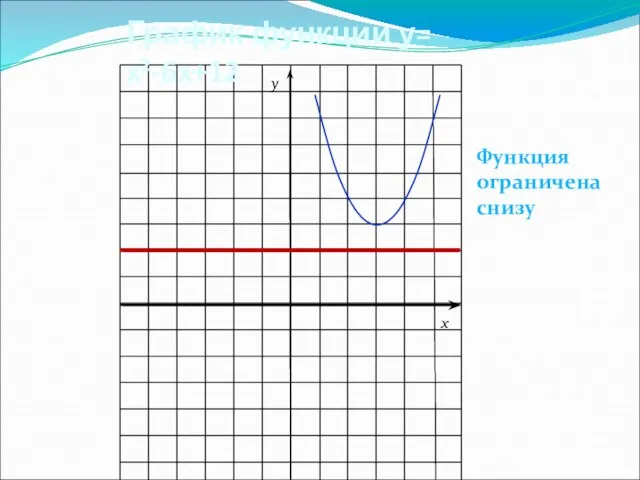
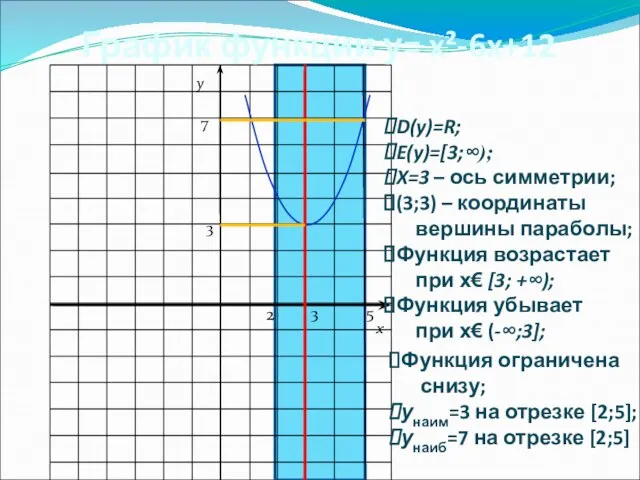
График функции у= x²-6x+12
x
y
Функция ограничена снизу

График функции у= x²-6x+12
D(y)=R;
E(y)=[3;∞);
X=3 – ось симметрии;
(3;3) – координаты
вершины параболы;
Функция возрастает при х€ [3; +∞);
Функция убывает
при х€ (-∞;3];
Функция ограничена
снизу;
унаим=3 на отрезке [2;5];
унаиб=7 на отрезке [2;5]
3
3
7
5
2
x
y

Итог урока
отмечаются лучшие работы;
проводится анализ работ учащихся;
организуется самооценка учениками
своей деятельности;
фиксируется степень соответствия
поставленной цели и результатов
деятельности;
намечаются цели последующей
деятельности;
комментируется домашнее задание.

Домашнее задание
Построить графики функций и
описать их свойства:
y=2x2+4;
y=2(x+3)2-5;
y=1/2(x-6)2;
y=-3 x 2-6x+1.