Комплексный чертеж плоскости

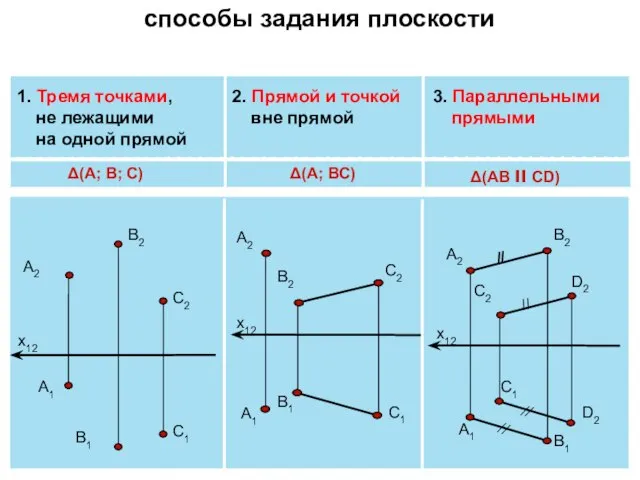
1. Тремя точками,
не лежащими
на одной прямой
2. Прямой и точкой вне прямой
3. Параллельными прямыми
Δ(А; В; С)
Δ(А; ВС)
Δ(АВ ll СD)
способы задания плоскости

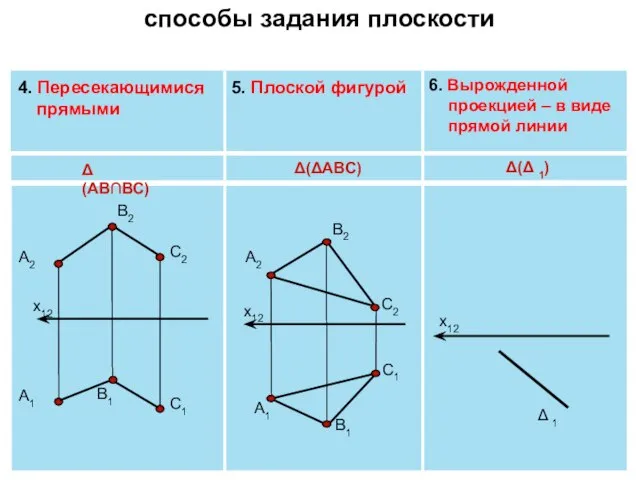
4. Пересекающимися прямыми
5. Плоской фигурой
6. Вырожденной проекцией – в виде прямой линии
х12
Δ(АВ∩ВС)
Δ(ΔАВС)
Δ(Δ 1)
Δ 1
способы задания плоскости

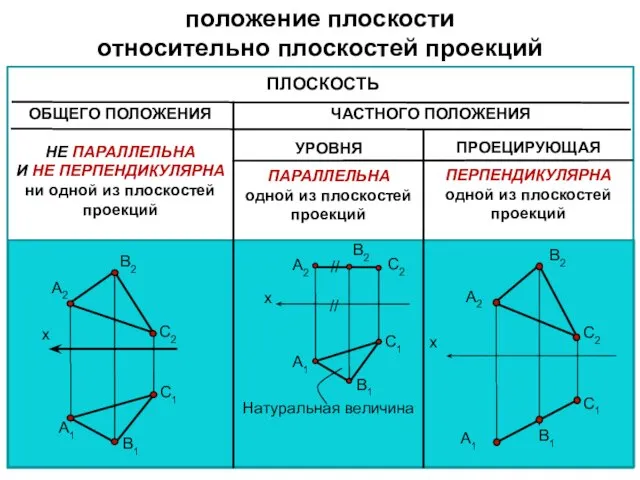
положение плоскости
относительно плоскостей проекций
ПЛОСКОСТЬ
ОБЩЕГО ПОЛОЖЕНИЯ ЧАСТНОГО ПОЛОЖЕНИЯ
УРОВНЯ
ПАРАЛЛЕЛЬНА
одной из плоскостей проекций
ПРОЕЦИРУЮЩАЯ
ПЕРПЕНДИКУЛЯРНА одной из плоскостей проекций
НЕ ПАРАЛЛЕЛЬНА
И НЕ ПЕРПЕНДИКУЛЯРНА
ни одной из плоскостей
проекций

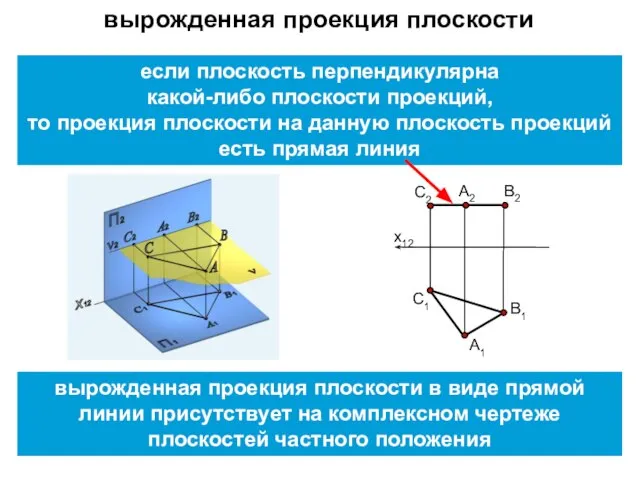
вырожденная проекция плоскости
вырожденная проекция плоскости в виде прямой линии присутствует на комплексном чертеже
плоскостей частного положения
если плоскость перпендикулярна
какой-либо плоскости проекций,
то проекция плоскости на данную плоскость проекций есть прямая линия

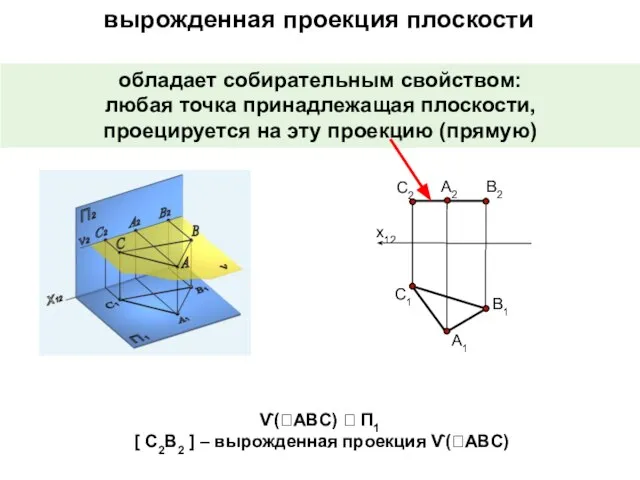
вырожденная проекция плоскости
обладает собирательным свойством:
любая точка принадлежащая плоскости,
проецируется на эту проекцию (прямую)
Ѵ(ABC)  П1
[ C2B2 ] – вырожденная проекция Ѵ(ABC)

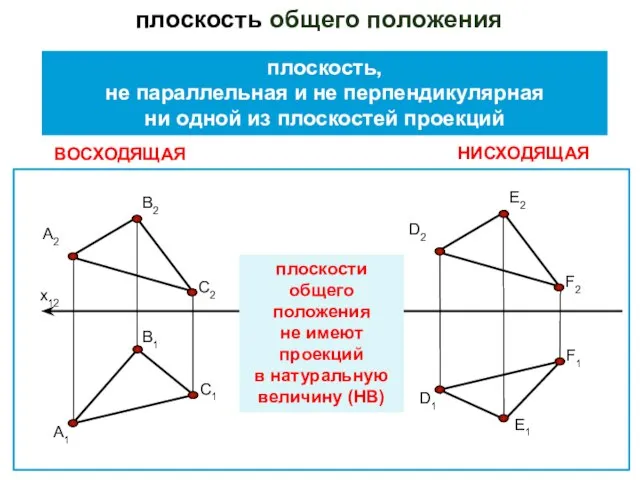
плоскость общего положения
ВОСХОДЯЩАЯ
НИСХОДЯЩАЯ
плоскость,
не параллельная и не перпендикулярная
ни одной из плоскостей проекций
плоскости общего положения
не имеют проекций
в натуральную величину (НВ)

ПЛОСКОСТИ
ЧАСТНОГО ПОЛОЖЕНИЯ

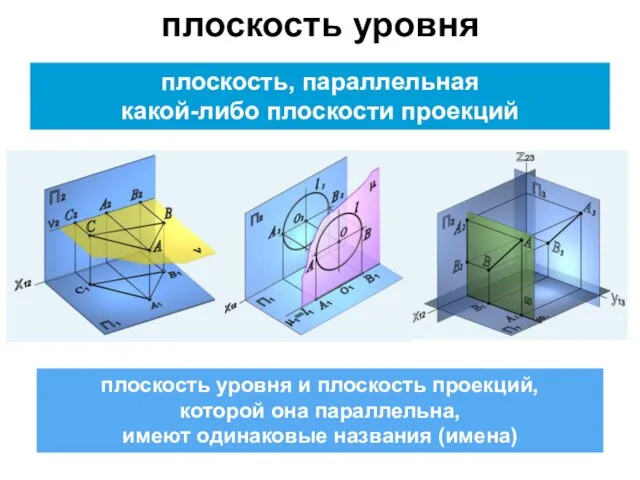
плоскость, параллельная
какой-либо плоскости проекций
плоскость уровня
плоскость уровня и плоскость проекций,
которой она параллельна,
имеют одинаковые названия (имена)

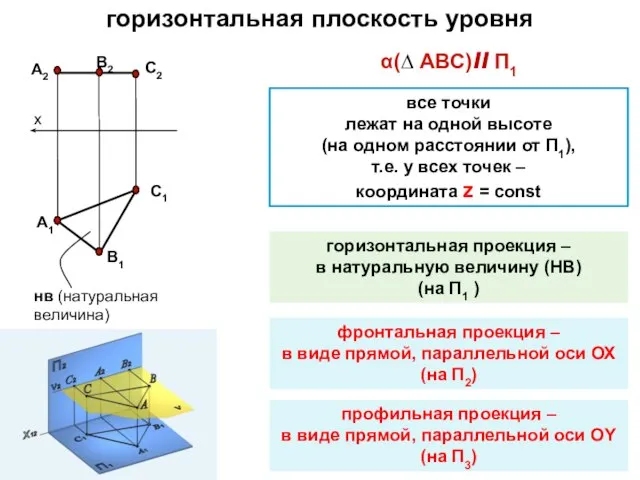
α(∆ АВС)ll П1
горизонтальная плоскость уровня
все точки
лежат на одной высоте
(на одном расстоянии от П1),
т.е. у всех точек –
координата z = const
горизонтальная проекция –
в натуральную величину (НВ)
(на П1 )
фронтальная проекция –
в виде прямой, параллельной оси ОХ
(на П2)
профильная проекция –
в виде прямой, параллельной оси ОY
(на П3)

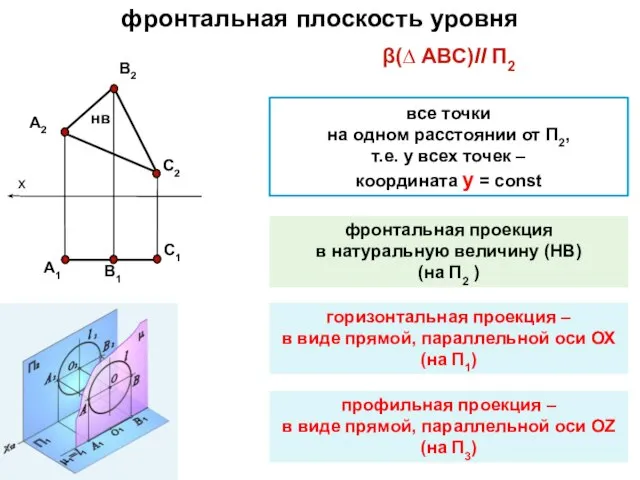
β(∆ АВС)ll П2
фронтальная плоскость уровня
х
все точки
на одном расстоянии от П2,
т.е. у всех точек –
координата y = const
фронтальная проекция
в натуральную величину (НВ)
(на П2 )
горизонтальная проекция –
в виде прямой, параллельной оси ОХ
(на П1)
профильная проекция –
в виде прямой, параллельной оси ОZ
(на П3)

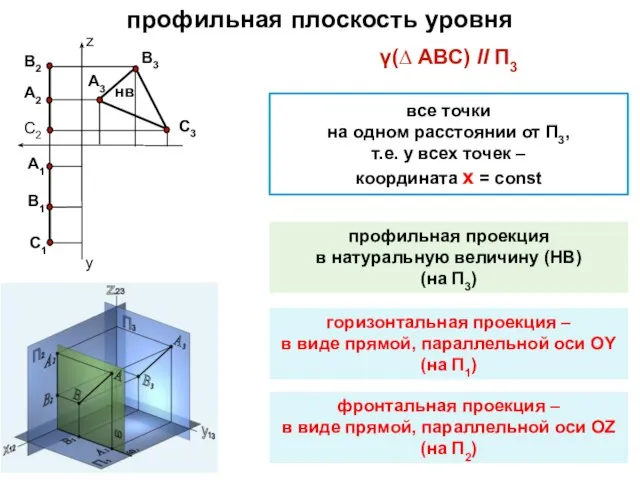
γ(∆ АВС) ll П3
профильная плоскость уровня
все точки
на одном расстоянии от П3, т.е. у всех точек –
координата х = const
профильная проекция
в натуральную величину (НВ)
(на П3)
горизонтальная проекция –
в виде прямой, параллельной оси ОY
(на П1)
фронтальная проекция –
в виде прямой, параллельной оси ОZ
(на П2)

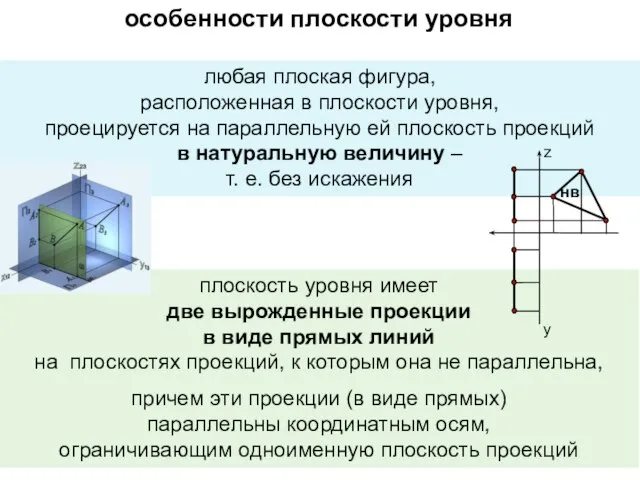
особенности плоскости уровня
любая плоская фигура,
расположенная в плоскости уровня,
проецируется на параллельную ей плоскость проекций
в натуральную величину –
т. е. без искажения
плоскость уровня имеет
две вырожденные проекции
в виде прямых линий
на плоскостях проекций, к которым она не параллельна,
причем эти проекции (в виде прямых)
параллельны координатным осям,
ограничивающим одноименную плоскость проекций

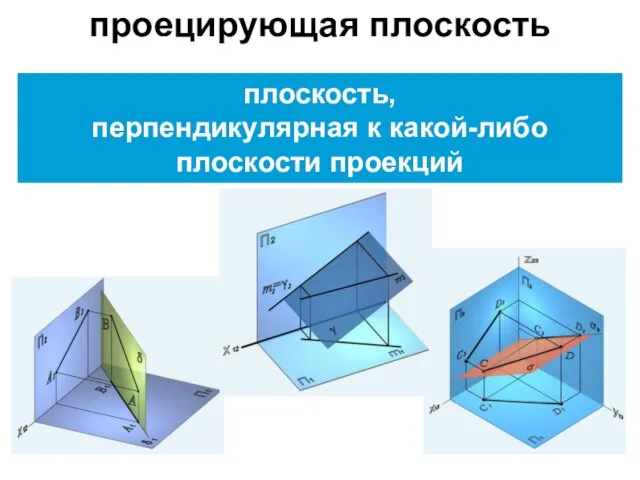
плоскость,
перпендикулярная к какой-либо плоскости проекций
проецирующая плоскость

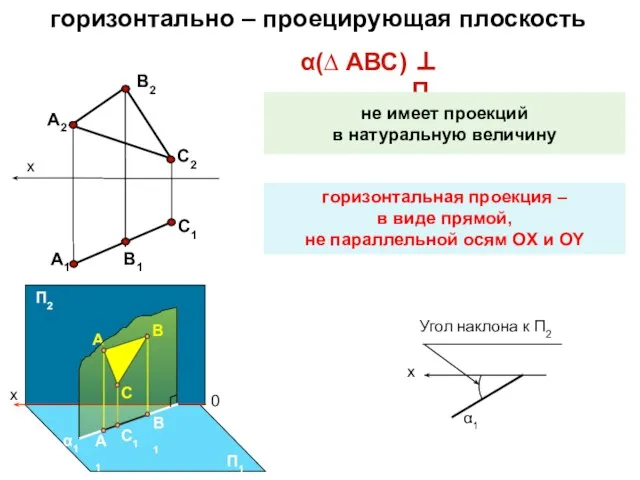
α(∆ АВС) ⊥ П1
горизонтально – проецирующая плоскость
не имеет проекций
в натуральную величину
горизонтальная проекция –
в виде прямой,
не параллельной осям OX и ОY

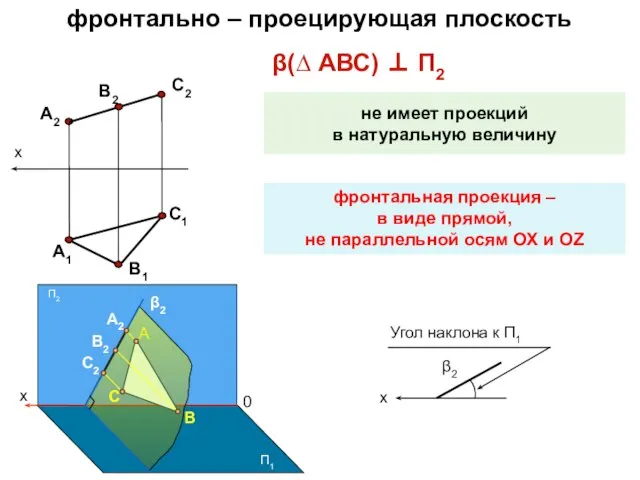
β(∆ АВС) ⊥ П2
фронтально – проецирующая плоскость
не имеет проекций
в натуральную величину
фронтальная проекция –
в виде прямой,
не параллельной осям OX и ОZ

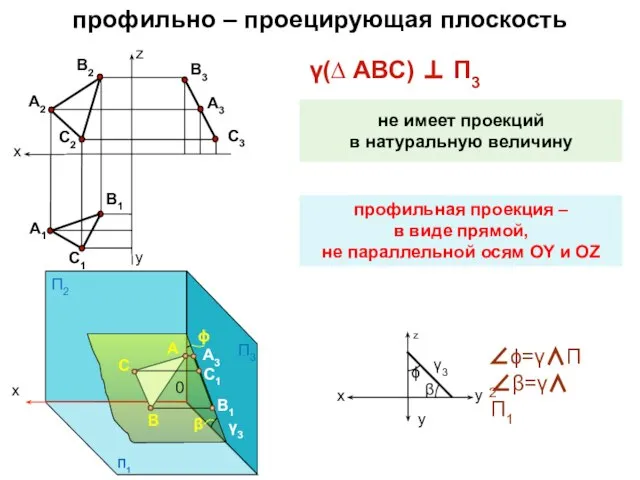
профильно – проецирующая плоскость
γ(∆ АВС) ⊥ П3
не имеет проекций
в натуральную величину
профильная проекция –
в виде прямой,
не параллельной осям OY и ОZ

особенности проецирующей плоскости
углы наклона проецирующей плоскости
к плоскостям проекций
проецируются в натуральную величину
на одноименной плоскости проекций
не имеет проекций
в натуральную величину
проецирующая плоскость имеет
одну вырожденную проекцию
в виде прямой линий
на плоскости проекций, к которой она перпендикулярна,
причем эта проекция (в виде прямой)
не параллельна координатным осям,
ограничивающим одноименную плоскость проекций

ПРИНАДЛЕЖНОСТЬ
ТОЧКИ и ПРЯМОЙ
ПЛОСКОСТИ

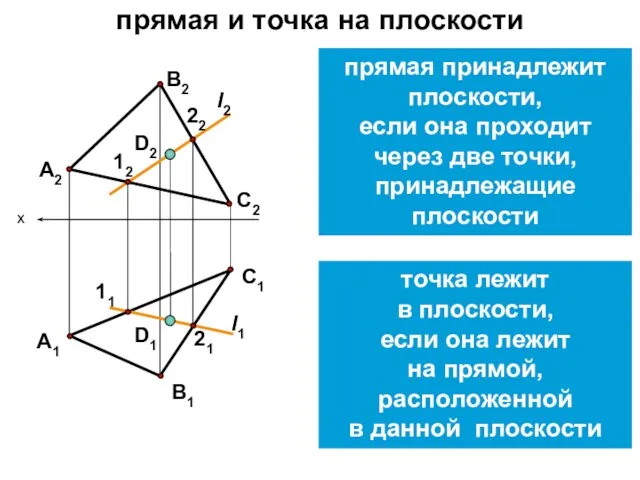
прямая и точка на плоскости
прямая принадлежит плоскости,
если она проходит через две точки, принадлежащие плоскости
точка лежит
в плоскости,
если она лежит
на прямой, расположенной
в данной плоскости

ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ

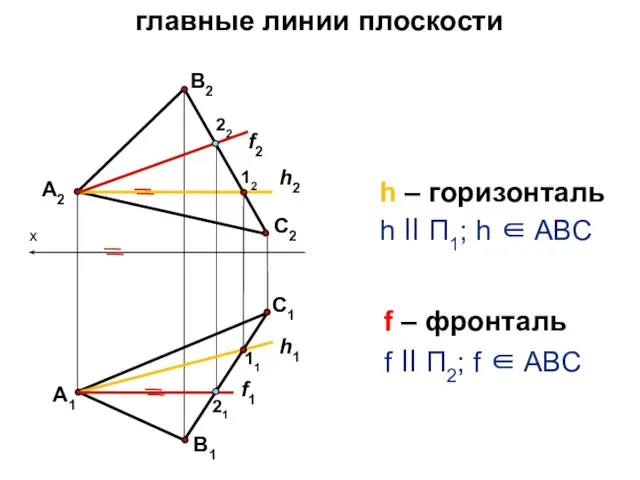
главные линии плоскости
h ll П1; h ∈ ABC
f ll П2; f ∈ ABC
х
А2
В2
С2
С1
А1
В1
h2
h1
12
22
11
21
f2
f1
//
h – горизонталь
f – фронталь
//
//

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ПРЯМОЙ И ПЛОСКОСТИ

а. Прямая принадлежит плоскости
б. Прямая параллельна плоскости
в. Прямая пересекает плоскость (частный случай – перпендикулярна плоскости)
варианты взаимного расположения
прямой и плоскости

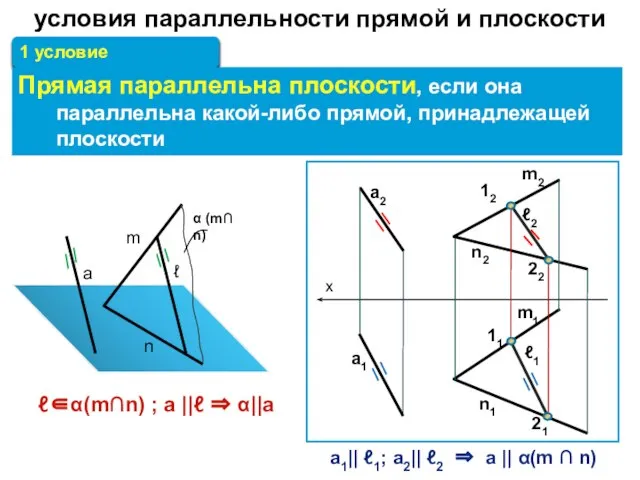
1 условие
Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей плоскости
ℓ∈α(m∩n) ; а ||ℓ ⇒ α||а
а1|| ℓ1; а2|| ℓ2 ⇒ а || α(m ∩ n)
условия параллельности прямой и плоскости

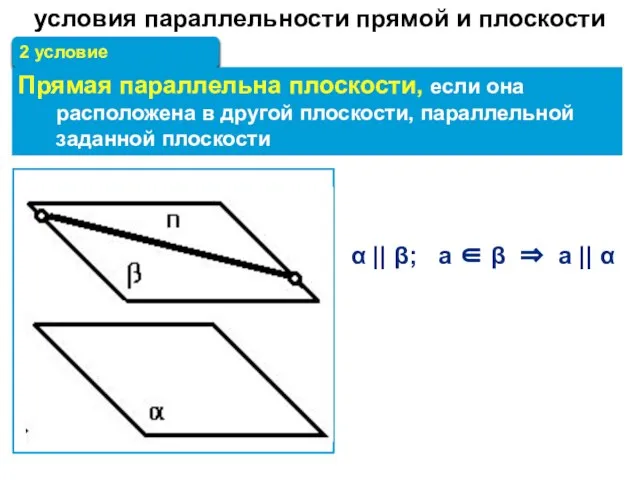
2 условие
Прямая параллельна плоскости, если она расположена в другой плоскости, параллельной заданной плоскости
условия параллельности прямой и плоскости
α || β; а ∈ β ⇒ а || α

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПЛОСКОСТЕЙ

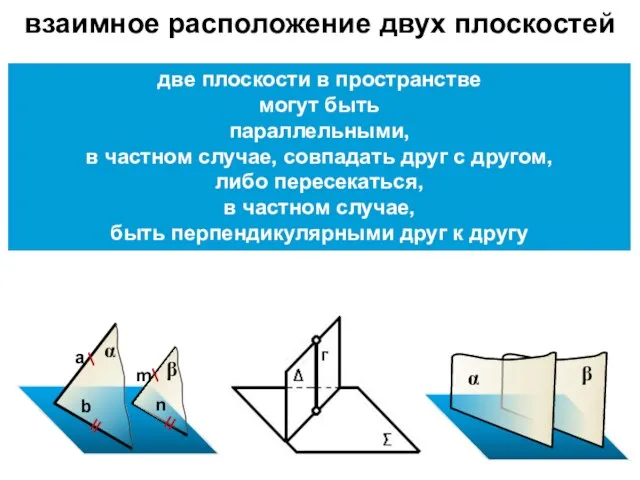
две плоскости в пространстве
могут быть
параллельными,
в частном случае, совпадать друг с другом,
либо пересекаться,
в частном случае,
быть перпендикулярными друг к другу
взаимное расположение двух плоскостей

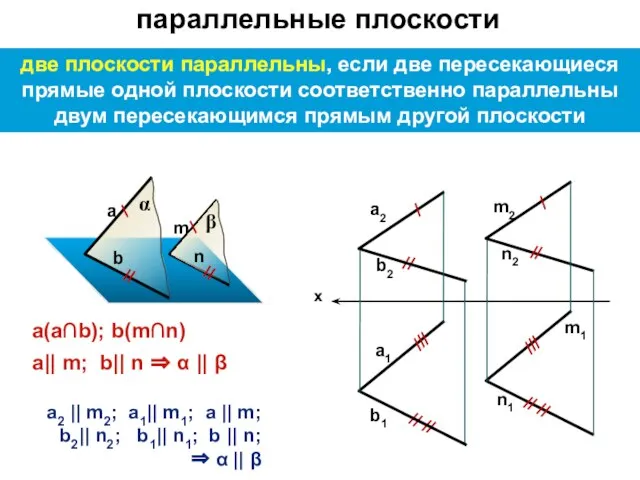
две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости
а2 || m2; a1|| m1; a || m;
b2|| n2; b1|| n1; b || n;
⇒ α || β
a(а∩b); b(m∩n)
а|| m; b|| n ⇒ α || β
параллельные плоскости