Содержание
- 2. На прошлой лекции Цифровая обработка сигналов Сигналы и системы Свертка Преобразование Фурье Спектр, высокие и низкие
- 3. На лекции Информация в изображении Предобработка изображения Удаление шума в цветных изображениях Удаление шума в бинарных
- 4. Обработка и анализ изображений Обработка изображений Image processing Компьютерное (машинное) зрение Computer (machine) vision Компьютерная графика
- 5. Изображение Изображение оптическое – картина, получаемая в результате прохождения через оптическую систему лучей, распространяющихся от объекта,
- 6. Компьютерное зрение Цель Принятие решений о реальных физических объектах и сценах, основываясь на воспринимаемых изображениях. Метод
- 7. Информация, содержащаяся в изображении Полезная информация Информация низкого уровня Области однородные по некому признаку Границы однородных
- 8. Предобработка изображения Подготовка изображения к анализу Подавление и устранение шума Упрощение изображения например, бинаризация Усиление и
- 9. Предобработка изображения Подавление и устранение шума Причины возникновения шума: Несовершенство измерительных приборов Хранение и передача изображений
- 10. Устранение шума в полутоновых и цветных изображениях Пример: изображение с равномерным шумом. noise(i,j) – нормально распределенная
- 11. Усреднение
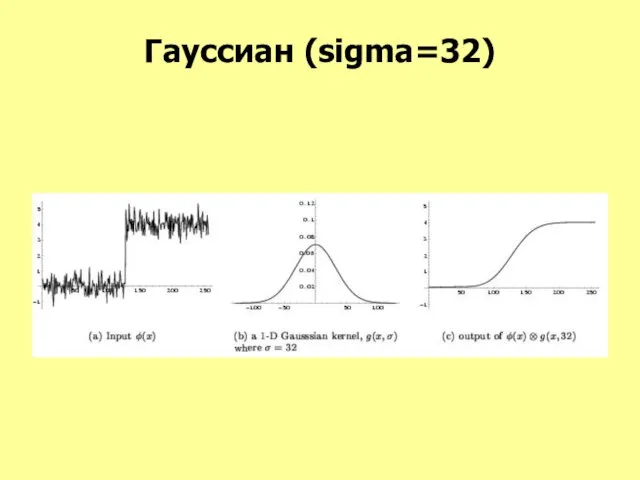
- 12. Гауссиан (sigma=32)
- 13. Размытие
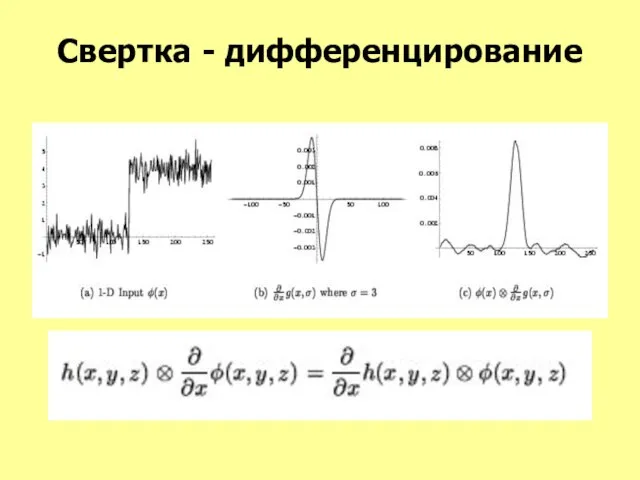
- 14. Свертка - дифференцирование
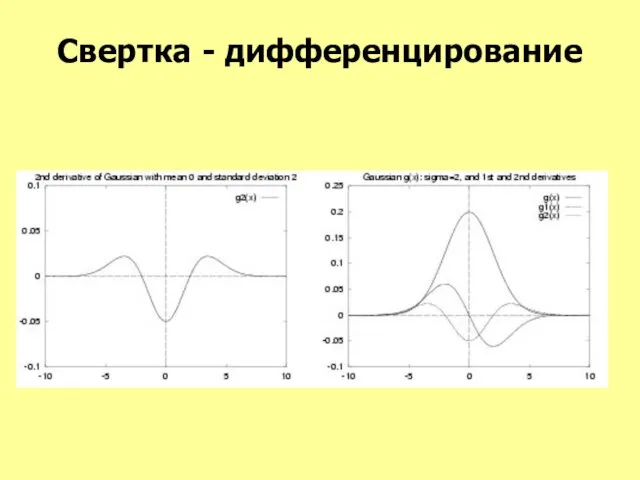
- 15. Свертка - дифференцирование
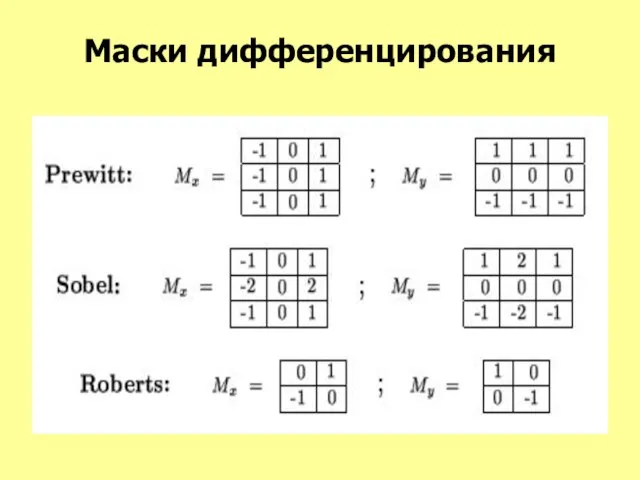
- 16. Маски дифференцирования
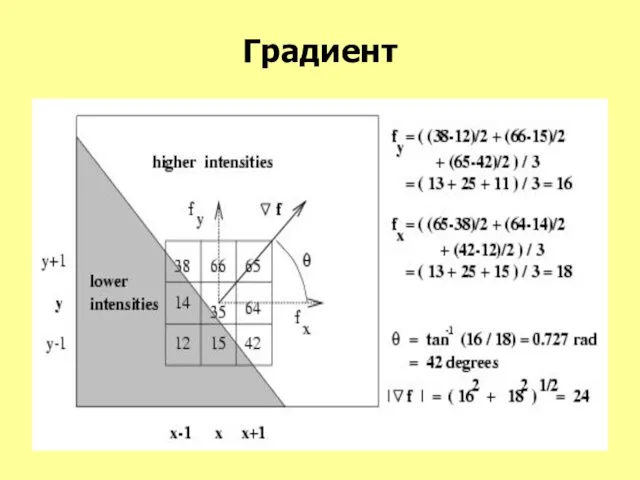
- 17. Градиент
- 18. Попикселная обработка Out[x, y] = f (In[x,y])
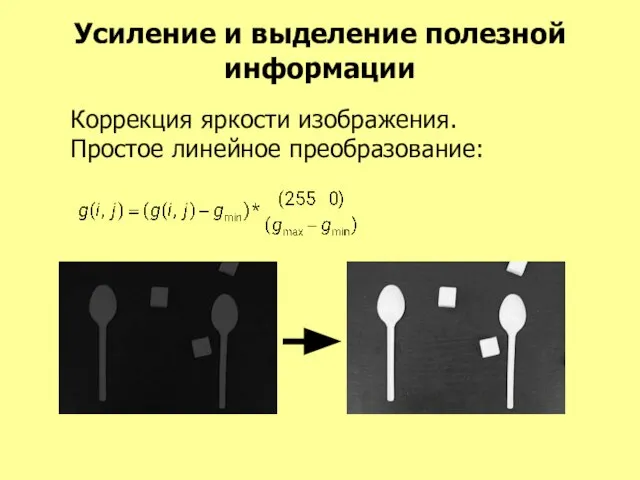
- 19. Усиление и выделение полезной информации Коррекция яркости изображения. Простое линейное преобразование:
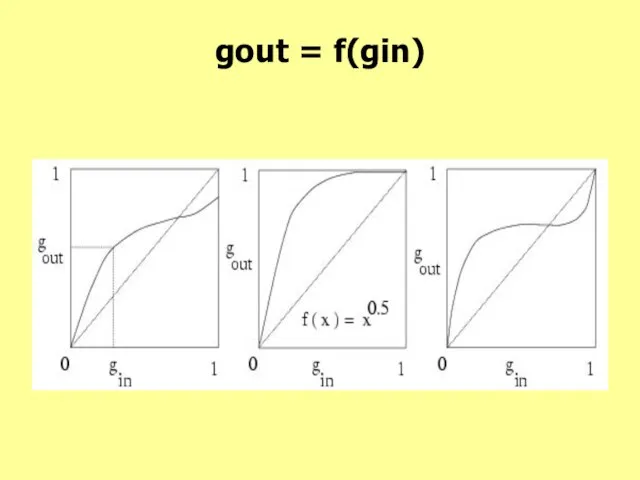
- 20. gout = f(gin)
- 21. gout = f(gin)
- 22. Выравнивание гистограмм Используются все n уровней серого цвета На каждый уровень попадает примерно одинаковое количество пикселей:
- 23. Выравнивание гистограмм
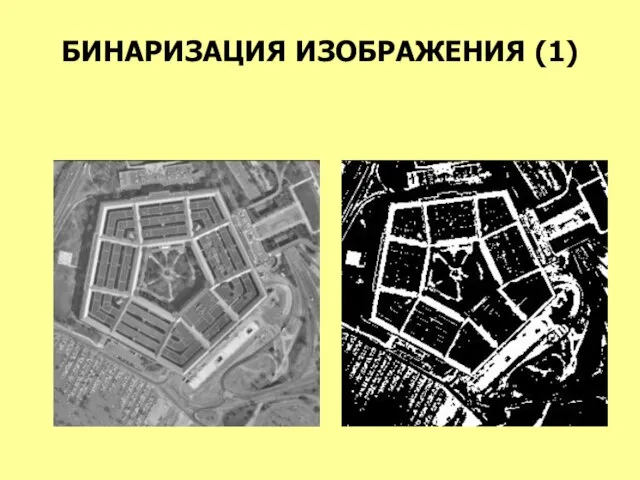
- 24. БИНАРИЗАЦИЯ ИЗОБРАЖЕНИЯ (1)
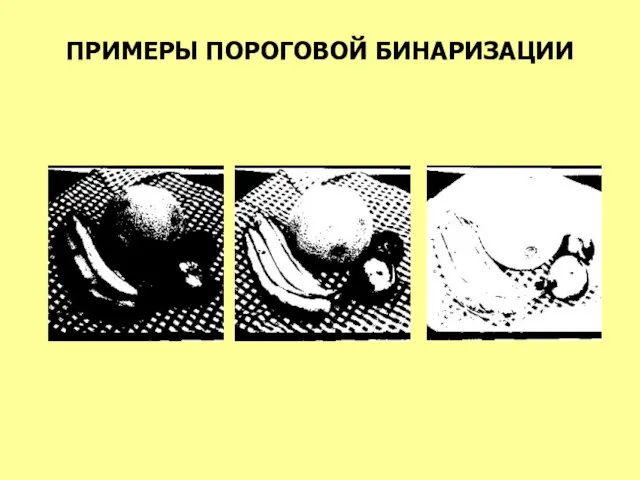
- 25. ПРИМЕРЫ ПОРОГОВОЙ БИНАРИЗАЦИИ
- 26. Подавление и устранение шума Устранение шума в бинарных изображениях Широко известный способ - устранение шума с
- 27. Устранение шума типа «соль и перец» Задача – избавиться от одиночных темных пикселей в светлых областях
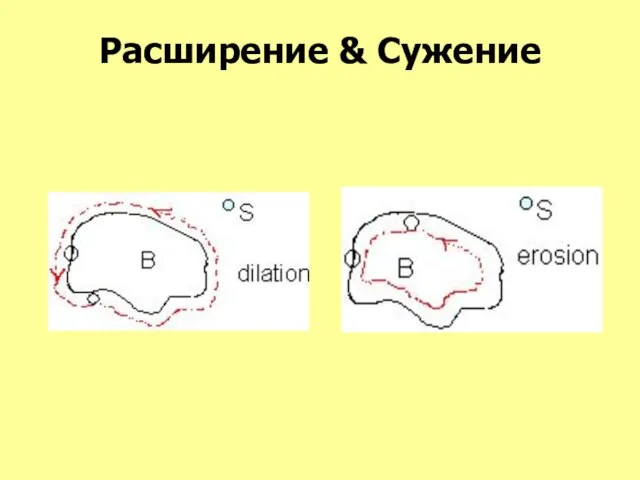
- 28. МОРФОЛОГИЧЕСКИЕ ФИЛЬТРЫ Сужение (Эрозия, Erosion) Расширение (Dilation) Закрытие (Closing) Раскрытие (Opening)
- 29. Морфологические операции
- 30. Расширение & Сужение
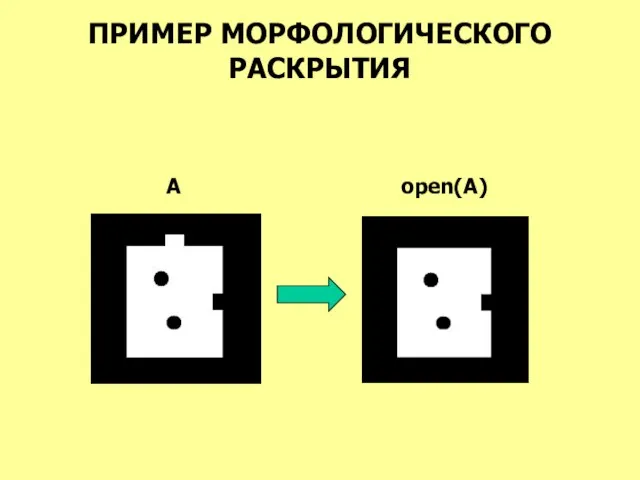
- 31. ПРИМЕР МОРФОЛОГИЧЕСКОГО РАСКРЫТИЯ A open(A)
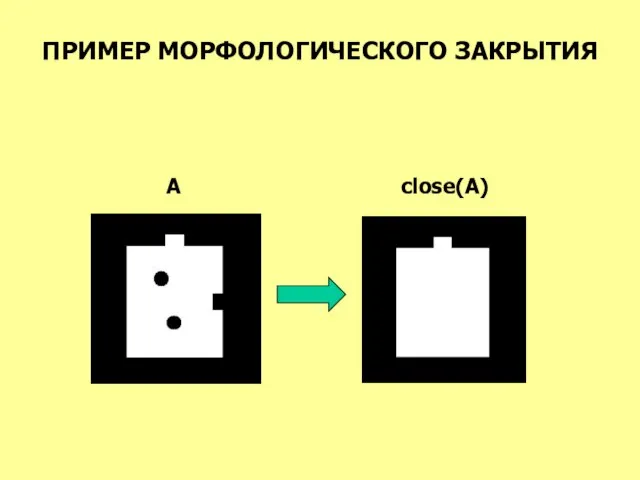
- 32. ПРИМЕР МОРФОЛОГИЧЕСКОГО ЗАКРЫТИЯ A close(A)
- 33. Морфологические операции
- 34. Устранение шума в бинарных изображениях Пример бинарного изображению с сильным шумом
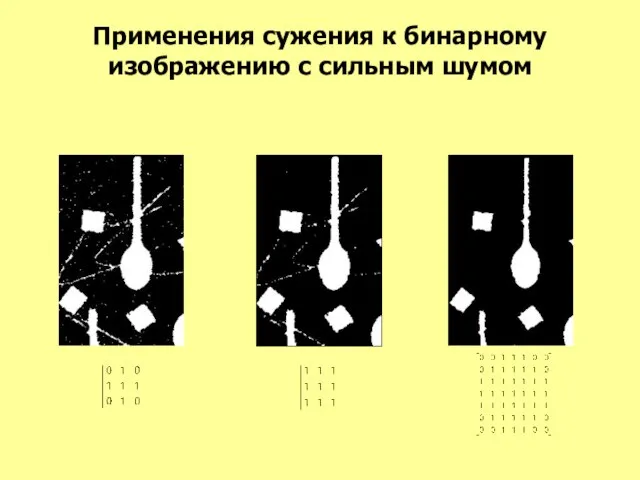
- 35. Применения сужения к бинарному изображению с сильным шумом
- 36. Устранение шума в бинарных изображениях Пример бинарного изображению с дефектами распознаваемых объектов
- 37. Не лучший пример для морфологии Не во всех случаях математическая морфология так легко убирает дефекты, как
- 38. Применения операции открытия
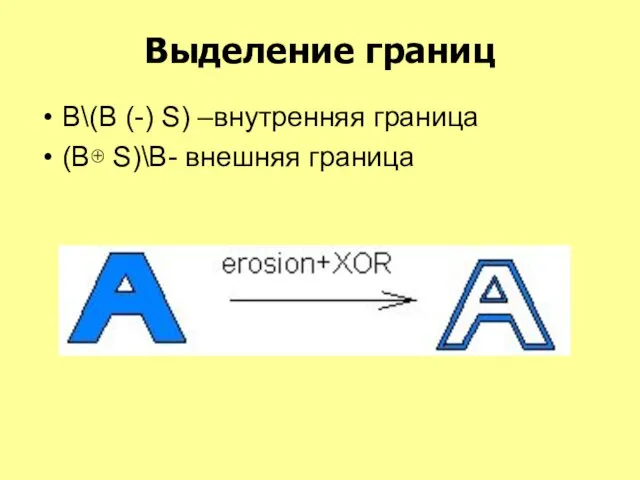
- 39. Выделение границ В\(B (-) S) –внутренняя граница (В⊕ S)\B- внешняя граница
- 40. ПРИМЕР ОКОНТУРИВАНИЯ ОБЪЕКТА
- 41. МОРФОЛОГИЧЕСКАЯ СКЕЛЕТИЗАЦИЯ Операция скелетонизации Операция де-скелетонизации
- 42. МОРФОЛОГИЧЕСКАЯ СКЕЛЕТИЗАЦИЯ
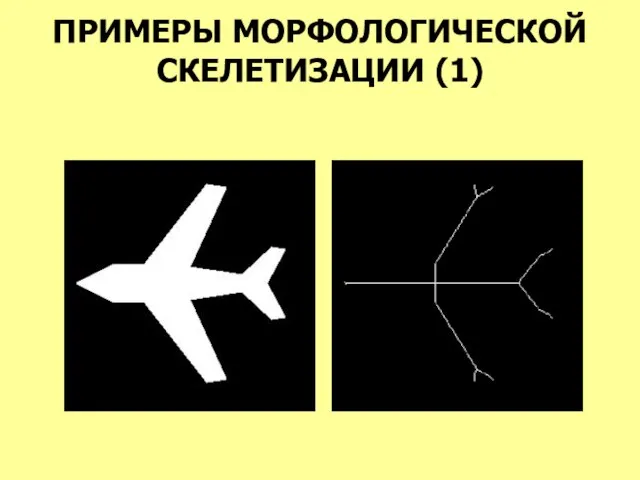
- 43. ПРИМЕРЫ МОРФОЛОГИЧЕСКОЙ СКЕЛЕТИЗАЦИИ (1)
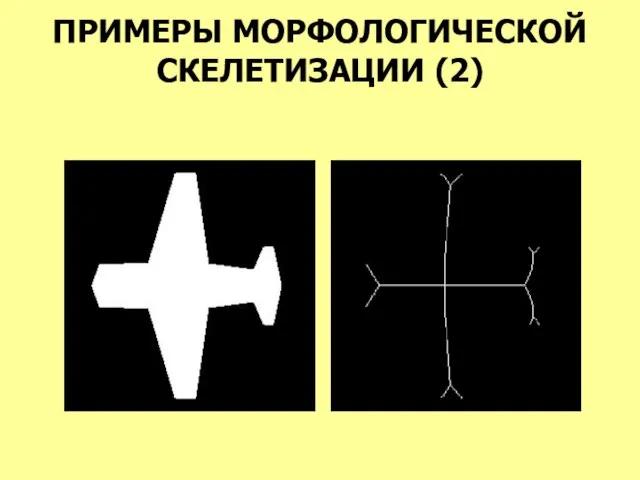
- 44. ПРИМЕРЫ МОРФОЛОГИЧЕСКОЙ СКЕЛЕТИЗАЦИИ (2)
- 45. Медианный фильтр Выбор медианы среди значений яркости пикселов в некоторой окрестности. Определение медианы: Медианный фильтр радиусом
- 46. Применение медианного фильтра Результат применения медианного фильтра с радиусом 5 пикселов Результат применения медианного фильтра с
- 47. Очистка изображения с помощью медианного фильтра Фильтр с радиусом 3x3
- 48. Очистка изображения с помощью медианного фильтра Фильтр с радиусом 3x3
- 49. Быстрая реализация медианного фильтра Медианный фильтр считается дольше, чем операция свертки, поскольку требует частичной сортировки массива
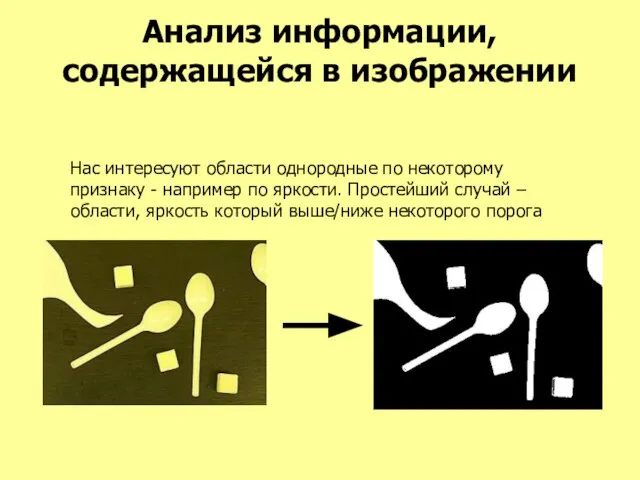
- 50. Анализ информации, содержащейся в изображении Нас интересуют области однородные по некоторому признаку - например по яркости.
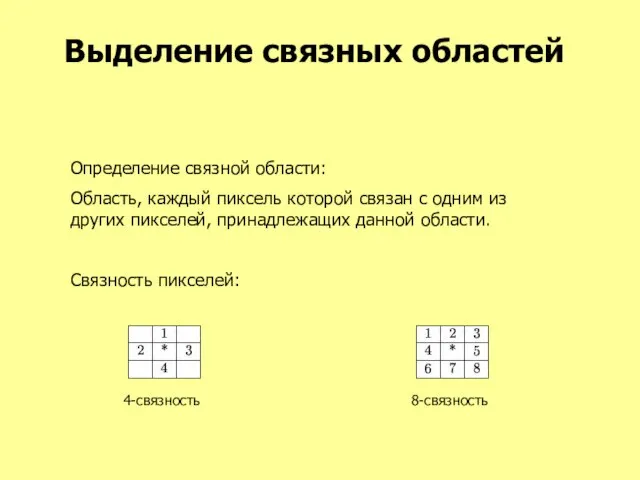
- 51. Выделение связных областей Определение связной области: Область, каждый пиксель которой связан с одним из других пикселей,
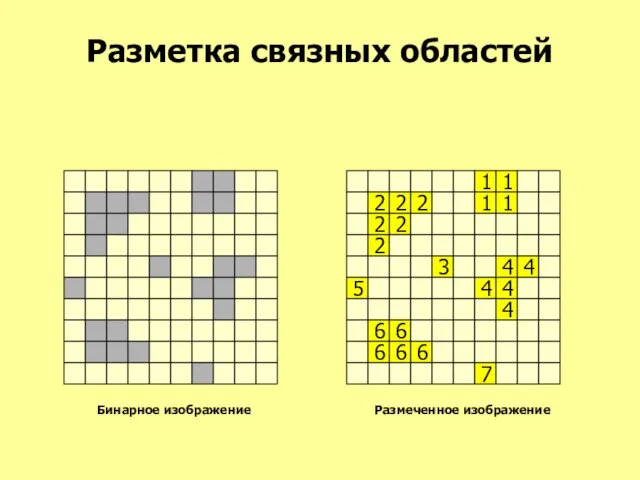
- 52. Разметка связных областей 1 1 2 2 2 1 1 2 2 2 3 4 4
- 53. Рекурсивная разметка связных областей (1) void Labeling(BIT* img[], int* labels[]) { // labels должна быть обнулена
- 54. Рекурсивная разметка связных областей (2) void Fill(BIT* img[], int* labels[], int x, int y, int L)
- 55. Разметка связных областей путем последовательного сканирования Последовательно, сканируем бинарное изображение сверху вниз, слева направо: if A
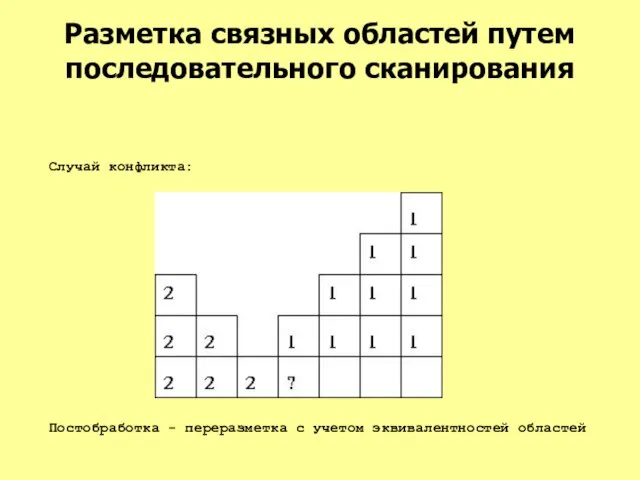
- 56. Разметка связных областей путем последовательного сканирования Случай конфликта: Постобработка - переразметка с учетом эквивалентностей областей
- 57. Анализ формы связных областей Для каждой области можно подсчитать некий набор простейших числовых характеристик: Площадь Периметр
- 58. Анализ формы связных областей Площадь – количество пикселей в области; Периметр – количество пикселей принадлежащих границе
- 59. Подсчет периметра области Пиксель лежит на границе области, если он сам принадлежит области и хотя бы
- 60. Пример периметров области Область Внутренняя граница Внешняя граница
- 61. Статистические моменты области Дискретный центральный момент mij области определяется следующим образом: n – общее количество пикселей
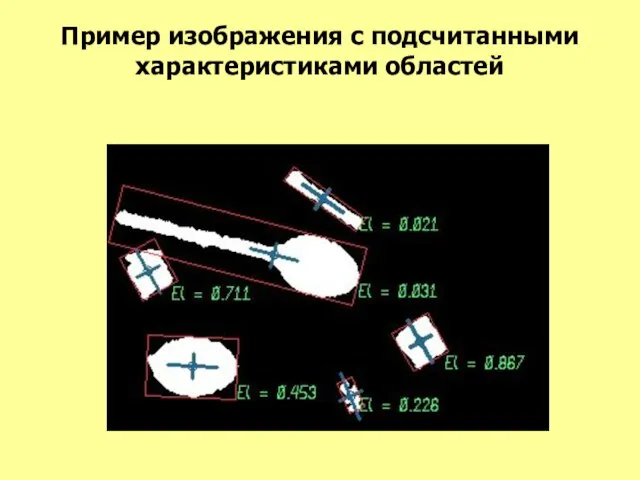
- 62. Инвариантные характеристики области Для распознавания нас интересуют характеристики инвариантные по отношению к масштабированию, переносу, повороту: Удлиненность,
- 63. Ориентация главной оси инерции Не является инвариантной к повороту, но в ряде случаев предоставляет полезную информацию
- 64. Пример изображения с подсчитанными характеристиками областей
- 65. Другие инвариантные характеристики области
- 66. Пример изображения для обработки
- 67. Литература http://graphics.cs.msu.su/ru/ library/cv/cv_intro.html http://graphics.cs.msu.su/ courses/cg2000b/notes/lect_1.doc
- 69. Скачать презентацию











![Попикселная обработка Out[x, y] = f (In[x,y])](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/368767/slide-17.jpg)




















![Рекурсивная разметка связных областей (1) void Labeling(BIT* img[], int* labels[]) { //](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/368767/slide-52.jpg)
![Рекурсивная разметка связных областей (2) void Fill(BIT* img[], int* labels[], int x,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/368767/slide-53.jpg)











 Живая и неживая природа.
Живая и неживая природа. Занятость и безработица
Занятость и безработица Ортологическая разминка
Ортологическая разминка Стратегический анализ внешней среды организации
Стратегический анализ внешней среды организации Салонные женские стрижки
Салонные женские стрижки Пермский филиал ГУ ВШЭ Архипов Валерий Михайлович, зам. директора ПФ ГУ-ВШЭ, доцент каф.фин.менеджмента ПФ ГУ-ВШЭ. Ведерников Серге
Пермский филиал ГУ ВШЭ Архипов Валерий Михайлович, зам. директора ПФ ГУ-ВШЭ, доцент каф.фин.менеджмента ПФ ГУ-ВШЭ. Ведерников Серге Фотоэффект (11 класс)
Фотоэффект (11 класс) Что такое мастер-класс?
Что такое мастер-класс? ВЫСТУПЛЕНИЕ РУКОВОДИТЕЛЯ ГМО Белковой Елены Александровны
ВЫСТУПЛЕНИЕ РУКОВОДИТЕЛЯ ГМО Белковой Елены Александровны Выбор и обоснование выбора материала для ________________. Образец презентации по материаловедению
Выбор и обоснование выбора материала для ________________. Образец презентации по материаловедению Оценка и развитие бизнеса
Оценка и развитие бизнеса Ambient Media Что это такое? Что это такое? Ambient против классик и Ambient против классик и Эффективност ь Эффективност ь For ex. For ex. Вывод ы Вывод
Ambient Media Что это такое? Что это такое? Ambient против классик и Ambient против классик и Эффективност ь Эффективност ь For ex. For ex. Вывод ы Вывод Оценка движимого имущества. Практика решения задач
Оценка движимого имущества. Практика решения задач Разделы информатики, используемые в олимпиадных задачах
Разделы информатики, используемые в олимпиадных задачах РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК
РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК В объятьях двух морей новый
В объятьях двух морей новый Итоги 2009 – 2010 учебного года в 1 – 4 классахПедсовет 30.08 .2010г.
Итоги 2009 – 2010 учебного года в 1 – 4 классахПедсовет 30.08 .2010г.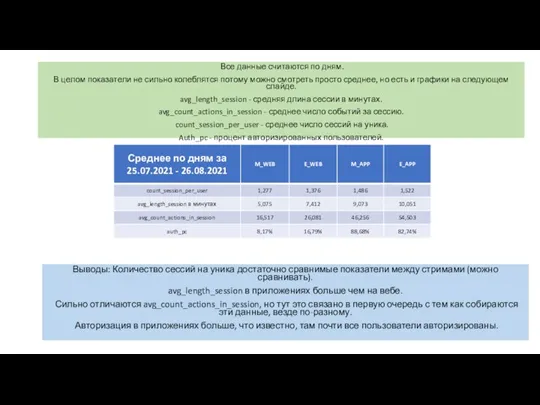 Количество сессий на уника
Количество сессий на уника Сказка о стране чисел
Сказка о стране чисел Актуальные проблемы литературы ХХ века и современной литературы
Актуальные проблемы литературы ХХ века и современной литературы Брейн-ринг Волшебные сказки
Брейн-ринг Волшебные сказки Стили в архитектуре
Стили в архитектуре O
O Мисс Филология
Мисс Филология Презентація Івкової Ольги ФГН-1,філологія, група 2
Презентація Івкової Ольги ФГН-1,філологія, група 2 Humor in advertising
Humor in advertising Презентация на тему Что мы знаем о тексте 5 класс
Презентация на тему Что мы знаем о тексте 5 класс Приготовление рабочих растворов
Приготовление рабочих растворов