Содержание
- 2. А1. Многовитковый плоский контур содержит N = 1000 витков тонкого провода. Контур квадратного сечения со стороной
- 3. Дано: e = q = 1,6⋅10-19 Кл m = 9,11⋅10-31 кг рm /L - ? А2.
- 4. А3. По тонкому стержню длиной l = 1 м равномерно распределен заряд q = 0,24 мКл.
- 5. А4. Из проволоки длиной l = 20 см сделаны квадратный и круговой контуры. Найти вращающие моменты
- 6. А5. (В.11.61) На расстоянии а = 20 см от длинного прямолинейного вертикального проводника на длинной упругой
- 7. 6. Квадратная рамка с площадью S = 10−4 м2 содержит N = 400 витков тонкого провода.
- 8. А7. Квадратная рамка со стороной длиной а = 1 см, содержащая N = 200 витков тонкого
- 9. А8. (В.11.60) Катушка гальванометра, состоящая из N = 400 витков тонкой проволоки, намотанной на прямоугольный каркас
- 10. Дано: a = 2 cм b = 1 cм N = 1000 H = 100 A/м
- 11. A10. Однородный медный диск А радиусом R = 5 см помещен в магнитное поле с индукцией
- 13. Скачать презентацию
Слайд 2А1. Многовитковый плоский контур содержит N = 1000 витков тонкого провода. Контур
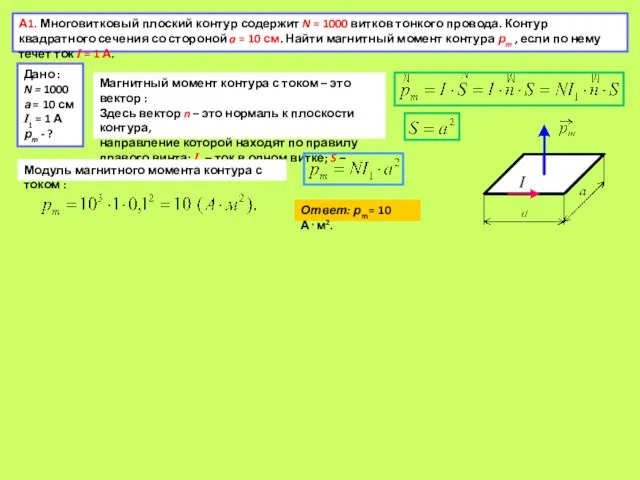
А1. Многовитковый плоский контур содержит N = 1000 витков тонкого провода. Контур
Дано :
N = 1000
а = 10 см
I1 = 1 А
рm - ?
Ответ: рm = 10 А⋅м2.
Магнитный момент контура с током – это вектор :
Здесь вектор n – это нормаль к плоскости контура,
направление которой находят по правилу правого винта; I1 – ток в одном витке; S – площадь витка.
Модуль магнитного момента контура с током :
Слайд 3Дано:
e = q = 1,6⋅10-19 Кл
m = 9,11⋅10-31 кг
рm /L - ?
Дано:
e = q = 1,6⋅10-19 Кл
m = 9,11⋅10-31 кг
рm /L - ?

А2. (Ч.22.18) Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Найти отношение магнитного момента рm эквивалентного кругового тока к моменту импульса L орбитального движения электрона. Указать направления векторов магнитного момента и момента импульса .
Знак минус «–» показывает, что векторы магнитного и механического моментов направлены в противоположные стороны.
Магнитный момент контура с током :
Направление вектора нормали n к плоскости контура
находится по правилу правого винта; S – площадь витка.
Модуль магнитного момента контура с током :
Движение электрона по круговой орбите представим как контурный ток с величиной :
(1)
(2)
Подставим (1) в (2) и получим окончательную формулу для магнитного момента :
Момент импульса электрона, движущегося по окружности относительно центра орбиты (направление вектора находится по правилу правого винта):
(3)
(4)
(5)
Найдем
отношение:
Слайд 4А3. По тонкому стержню длиной l = 1 м равномерно распределен заряд
А3. По тонкому стержню длиной l = 1 м равномерно распределен заряд

Дано:
q = 0,24 мКл
l = 1 м
= 100 рад/c
Рm - ?
Ответ: рm = 10–3 А⋅м2
Вращение распределенного по стержню заряда представим совокупностью круговых токов, имеющих радиус траектории r, изменяющийся от нуля до l/2.
Элементарный заряд dq, сосредоточенный на отрезке dl :
Круговой ток, образованный вращающимся с угловой скоростью ω зарядом dq :
Магнитный момент, созданный вращающимся элементарным током :
Модуль магнитного момента вращающегося элементарного тока :
Результирующий (суммарный) модуль магнитного момента всего вращающегося стержня :
Слайд 5А4. Из проволоки длиной l = 20 см сделаны квадратный и круговой
А4. Из проволоки длиной l = 20 см сделаны квадратный и круговой

Дано:
l = 0,2 м
В = 0,1 Тл
I = 2 А
= 45°
М1, М2 - ?
Механический вращающий момент сил М, действующий на рамку стоком I, помещенную в магнитное поле с индукцией В :
(вектор М перпендикулярен векторам В и рm , т.е. М⊥В и М⊥ рm)
Модуль вращающего момента сил :
(β - угол между векторами рm и В)
Углы α и β дополняют друг друга до прямого угла (α + β = 90о), поэтому модуль момента сил (2) перепишется в виде :
Площади квадратного контура и круглого контуров равной длины:
(1)
(2)
(3)
(4)
Подставим (4) в (3) :
Слайд 6А5. (В.11.61) На расстоянии а = 20 см от длинного прямолинейного вертикального
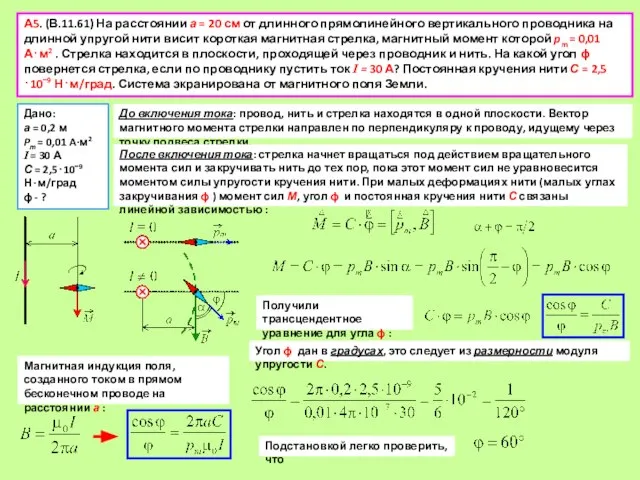
А5. (В.11.61) На расстоянии а = 20 см от длинного прямолинейного вертикального
Дано:
а = 0,2 м
Pm = 0,01 A∙м2
I = 30 А
С = 2,5⋅10−9
Н⋅м/град
ϕ - ?
До включения тока: провод, нить и стрелка находятся в одной плоскости. Вектор магнитного момента стрелки направлен по перпендикуляру к проводу, идущему через точку подвеса стрелки.
После включения тока: стрелка начнет вращаться под действием вращательного момента сил и закручивать нить до тех пор, пока этот момент сил не уравновесится моментом силы упругости кручения нити. При малых деформациях нити (малых углах закручивания ϕ ) момент сил М, угол ϕ и постоянная кручения нити С связаны линейной зависимостью :
Получили трансцендентное уравнение для угла ϕ :
Магнитная индукция поля, созданного током в прямом бесконечном проводе на расстоянии а :
Угол ϕ дан в градусах, это следует из размерности модуля упругости С.
Подстановкой легко проверить, что
Слайд 76. Квадратная рамка с площадью S = 10−4 м2 содержит N =
6. Квадратная рамка с площадью S = 10−4 м2 содержит N =

Дано:
S = 10−4 м2
N = 400
В = 0,03 Тл
I = 1 А
С = 10⋅10−6 Н⋅м/град
ϕ - ?
До включения тока: плоскость рамки параллельна вектору магнитной индукции. Вектор магнитного момента рамки перпендикулярен плоскости рамки согласно правилу правого винта.
После включения тока: рамка начнет вращаться под действием вращательного момента сил, действующих со стороны магнитного поля, и будет закручивать нить до тех пор, пока этот момент сил не уравновесится моментом силы упругости кручения нити. При малых деформациях нити (малых углах закручивания ϕ ) момент сил М, угол ϕ и постоянная кручения нити С связаны линейной зависимостью :
Получаем трансцендентное уравнение для угла ϕ :
Угол ϕ дан в градусах, это следует из размерности модуля упругости С.
Подстановкой легко проверить, что
Слайд 8А7. Квадратная рамка со стороной длиной а = 1 см, содержащая N
А7. Квадратная рамка со стороной длиной а = 1 см, содержащая N

Дано:
а = 1 cм
N = 200
В = 0,03 Тл
I = 1 А
С = 10⋅10−6 Н⋅м/град
ϕ -?
До включения тока: плоскость рамки перпендикулярна вектору магнитной индукции, а также - вектору магнитного момента рамки по правилу правого винта. Вектор магнитного момента рамки с током направлен навстречу вектору магнитной индукции (неустойчивое равновесие рамки).
После включения тока: рамка начнет вращаться под действием вращательного момента сил, действующих со стороны магнитного поля, и будет закручивать нить до тех пор, пока этот момент сил не уравновесится моментом силы упругости кручения нити. При малых деформациях нити (малых углах закручивания ϕ ) момент сил М, угол ϕ и постоянная кручения нити С связаны линейной зависимостью :
Получаем трансцендентное уравнение для угла ϕ :
Угол ϕ дан в градусах, это следует из размерности модуля упругости С.
Подстановкой легко проверить, что
Слайд 9А8. (В.11.60) Катушка гальванометра, состоящая из N = 400 витков тонкой проволоки,
А8. (В.11.60) Катушка гальванометра, состоящая из N = 400 витков тонкой проволоки,

Дано:
N = 400
а = 3 см
b= 2 см
В = 0,1 Тл
I = 0,1 А
ϕ1 = 0
ϕ 2 = 60°
М1, М2 - ?
Получаем окончательное выражение для модуля вращательного момента сил, действующих на рамку со стороны магнитного поля :
Вращающийся момент сил М, действующий на катушку:
Углы ϕ и α дополняют друг друга до прямого угла :
Магнитный момент рамки с током и ее площадь :
Перейдем к модулю вращательного момента сил, действующих на рамку с током со стороны магнитного поля :
Слайд 10Дано:
a = 2 cм
b = 1 cм
N = 1000
H = 100
Дано:
a = 2 cм
b = 1 cм
N = 1000
H = 100

С = 10−8 Н⋅м/град
= 0,5°
μ = 1
I - ?
A9. Катушка гальванометра, состоящая из N = 1000 витков проволоки, подвешена на упругой длинной нити в магнитном поле напряженностью Н = 100 А/м так, что ее плоскость параллельна направлению магнитного поля. Длина рамки катушки а = 2 см и ширина b = 1 см. Какой ток I течет по обмотке катушки, если катушка повернулась на угол ϕ = 0,5°? Постоянная кручения материала нити С = 10−8 Н⋅м/град.
Углы ϕ и α дополняют друг друга до прямого угла. Магнитный момент рамки с током pm и ее площадь S:
Окончательная формула для модуля вращательного момента сил, действующих на рамку со стороны магнитного поля :
Модуль вращательного момента сил, действующих на рамку с током со стороны магнитного поля :
До включения тока: плоскость рамки параллельна вектору магнитной индукции. Вектор магнитного момента рамки перпендикулярен плоскости рамки (правило правого винта).
После включения тока: рамка вращается под действием момента сил со стороны магнитного поля до тех пор, пока этот момент сил не уравновесит момент силы упругости кручения нити.
При малых деформациях нити (малые углы закручивания ϕ) момент сил М, угол ϕ и постоянная кручения нити С связаны линейной зависимостью :
Связь индукции и напряженности магнитного поля :
Учтем малость угла ϕ (cos 0,5° ≅ 1) и найдем ток :
Слайд 11A10. Однородный медный диск А радиусом R = 5 см помещен в
A10. Однородный медный диск А радиусом R = 5 см помещен в

(a, b – скользящие контакты). Найти вращающий момент, действующий на диск, и мощность такого двигателя.
Дано:
R = 5 cм
B = 0,2 Тл
I = 5 А
М - ? P - ?
Ток между контактами (a, b) примем линейным, поскольку ток течет по пути наименьшего сопротивления. Точка b диска закреплена, точка a диска вращается в направлении вектора линейной скорости v. Сила dF со стороны магнитного поля, действующая на элемент dr токопроводящего участка ab диска (α = π/2 - угол между векторами dr и В):
Вращающий момент, действующий на элемент dr участка ab, находящийся на расстоянии r от оси вращения ( β = π/2 - угол между векторами r и dF ) :
Вращающий момент, действующий на весь токопроводящий участок ab диска:
Приращение потока магнитного поля через поверхность, описываемую радиусом диска ab за один оборот :
Частота f и угловая скорость ω вращения диска :
Число оборотов диска за время t :
Общее изменение потока за время t :
Работа, совершаемая за время t :
Мощность двигателя :
- Не дана угловая скорость ω вращения.
 МОУ «Вейделевская СОШ»
МОУ «Вейделевская СОШ» 20140210_prezentatsiya1_2
20140210_prezentatsiya1_2 КОНЦЕПЦИЯ ДЕМОНСТРАЦИОННЫХ ПРОЕКТОВ по внедрению на местном уровне комплексного подхода к управлению жилищным фондом
КОНЦЕПЦИЯ ДЕМОНСТРАЦИОННЫХ ПРОЕКТОВ по внедрению на местном уровне комплексного подхода к управлению жилищным фондом Транспортировка документов организаций, как государственных, так и частных
Транспортировка документов организаций, как государственных, так и частных Презентация на тему Сибирь. Тайга (3 класс)
Презентация на тему Сибирь. Тайга (3 класс) Chef's eleven
Chef's eleven Песочная терапия как одна из технологий здоровьесбережения в работе логопеда
Песочная терапия как одна из технологий здоровьесбережения в работе логопеда Интервью с предпринимателем
Интервью с предпринимателем Респираторы
Респираторы Urok_5_Domashniy_skot
Urok_5_Domashniy_skot Системы охлаждения турбины
Системы охлаждения турбины Прабабушкины игры. Игра в лодыжки
Прабабушкины игры. Игра в лодыжки Легкая промышленность
Легкая промышленность Детская школа искусств в структуре жилого многофункционального комплекса
Детская школа искусств в структуре жилого многофункционального комплекса Система межведомственного электронного взаимодействия как важнейший фактор построения электронного правительства в Красноярск
Система межведомственного электронного взаимодействия как важнейший фактор построения электронного правительства в Красноярск Государственная собственность: О чем говорят опросы? и Какие направления важны для КУ? Т.Г. Долгопятова Институт анализа предпр
Государственная собственность: О чем говорят опросы? и Какие направления важны для КУ? Т.Г. Долгопятова Институт анализа предпр Опыт развития поликультурного образования в России: характерные черты, принципы, особенности
Опыт развития поликультурного образования в России: характерные черты, принципы, особенности Пюре моментального приготовления в стаканчиках Июль 2011.
Пюре моментального приготовления в стаканчиках Июль 2011. Вещество, образованное атомами разных химических элементов называют…
Вещество, образованное атомами разных химических элементов называют… Использование наглядности на уроках русского языка
Использование наглядности на уроках русского языка Динамика развития коммуникативной компетентности студентов-филологов в классическом университете
Динамика развития коммуникативной компетентности студентов-филологов в классическом университете ОБЛАКА
ОБЛАКА Несклоняемые имена существительные и их род
Несклоняемые имена существительные и их род Импульс потенциаль ная путь тяготения механика Кинематика Движение без анализа причин Динамика Причины движения скорость переме
Импульс потенциаль ная путь тяготения механика Кинематика Движение без анализа причин Динамика Причины движения скорость переме Супрематизм Казимира Малевича
Супрематизм Казимира Малевича Достижение цели – семь шагов, позволяющих ускорить процесс
Достижение цели – семь шагов, позволяющих ускорить процесс Мы идем в поход
Мы идем в поход Лицензированная школа маникюра Ladoni
Лицензированная школа маникюра Ladoni