Содержание
- 2. Примеры Менеджер интересуется, зависит ли объем продаж в этом месяце от объема рекламы в этом же
- 3. Постановка проблемы Наша цель – научиться отвечать на четыре вопроса: Вопрос 1. Существует ли связь между
- 4. Методы Корреляция – статистический метод, позволяющий определить, существует ли зависимость между переменными и на сколько она
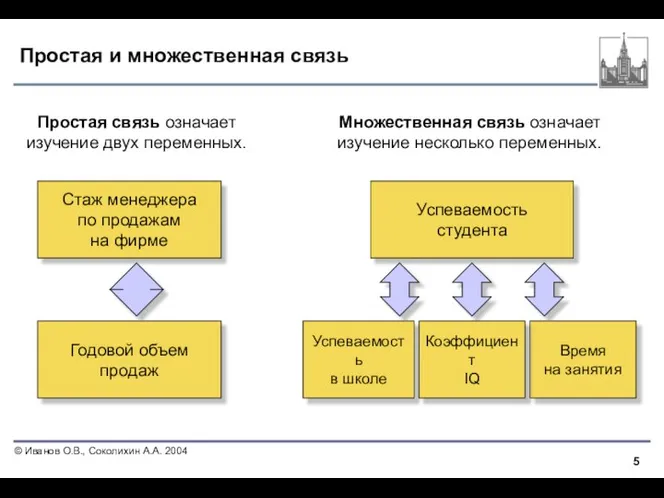
- 5. Простая и множественная связь Множественная связь означает изучение несколько переменных. Простая связь означает изучение двух переменных.
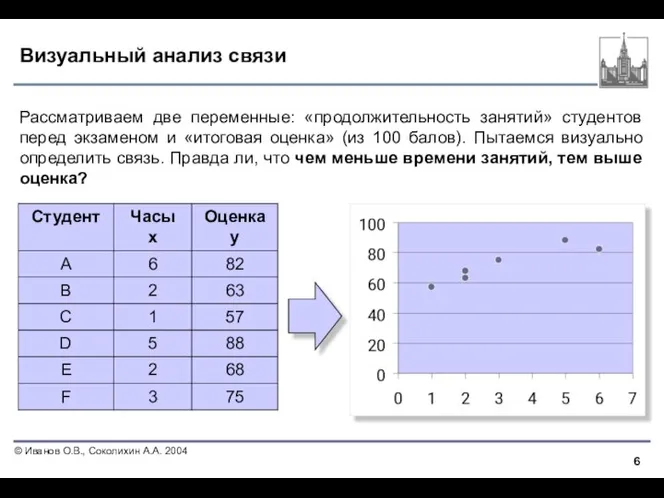
- 6. Визуальный анализ связи Рассматриваем две переменные: «продолжительность занятий» студентов перед экзаменом и «итоговая оценка» (из 100
- 7. Независимая и зависимая переменные Независимая переменная – это та переменная в регрессии, которую можно изменять. В
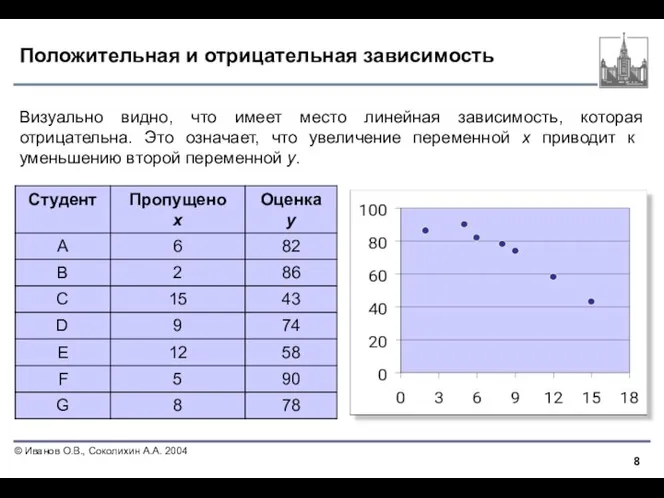
- 8. Положительная и отрицательная зависимость Визуально видно, что имеет место линейная зависимость, которая отрицательна. Это означает, что
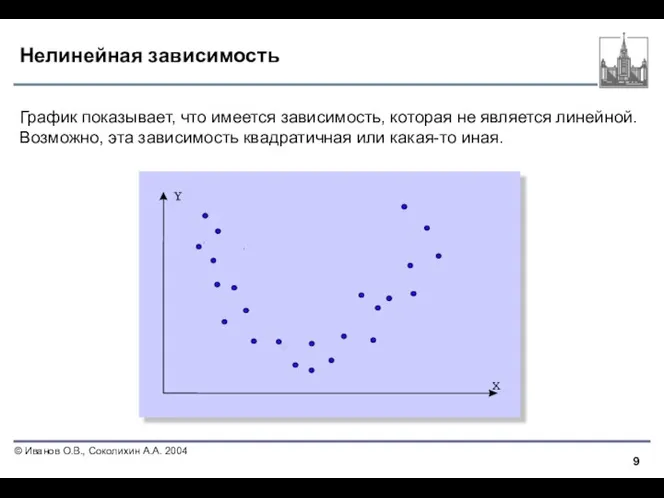
- 9. Нелинейная зависимость График показывает, что имеется зависимость, которая не является линейной. Возможно, эта зависимость квадратичная или
- 10. Отсутствие зависимости График сообщает нам об отсутствии зависимости продолжительности занятий в неделю от количества выпиваемого пива
- 11. * 12.1. Корреляция Связь между двумя переменными
- 12. Коэффициент корреляции Коэффициент корреляции измеряет силу и направление связи между двумя переменными. Обозначения: Выборочный коэффициент корреляции
- 13. Значения коэффициента корреляции Коэффициент корреляции изменяется на отрезке от –1 до +1. Если между переменными существует
- 14. Формула для вычисления r Коэффициент корреляции вычисляется по формуле: Это, так называемый, коэффициент корреляции Пирсона, равный
- 15. Вторая формула для вычисления r После несложных преобразований, из первой формулы можно получить другую формулу для
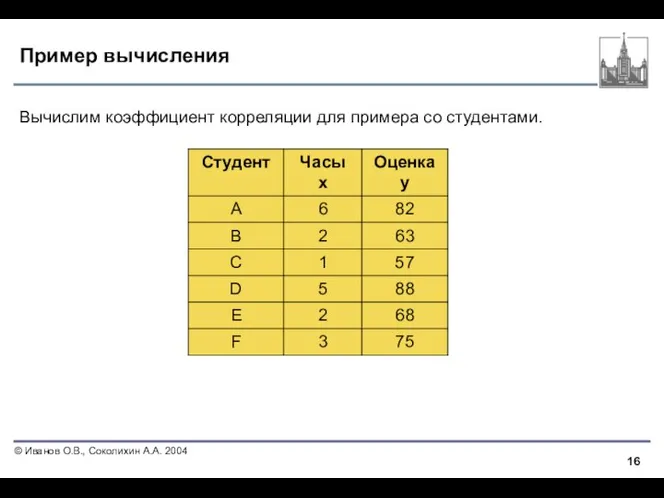
- 16. Пример вычисления Вычислим коэффициент корреляции для примера со студентами.
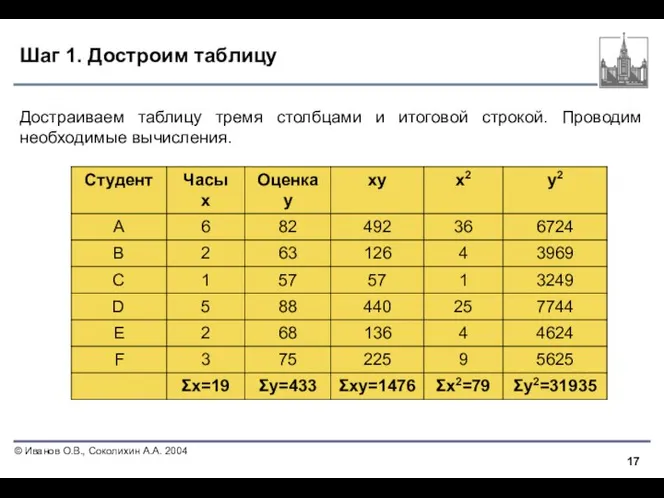
- 17. Шаг 1. Достроим таблицу Достраиваем таблицу тремя столбцами и итоговой строкой. Проводим необходимые вычисления.
- 18. Шаги 2-3. Подставим в формулу, получим ответ Подставим данные в формулу и найдем r : Ответ.
- 19. * 12.2. Значимость коэффициента корреляции Проверка гипотезы
- 20. Постановка проблемы Коэффициент корреляции генеральной совокупности ρ – это корреляция, вычисленная с использованием всевозможных пар значений
- 21. Последовательность действий Чтобы принять верное решение, воспользуемся процедурой проверки гипотезы. Она включает традиционные пять шагов: Шаг
- 22. Гипотезы Гипотезы сформулированы следующим образом. Основная гипотеза Н0: ρ = 0 Альтернативная гипотеза Н1: ρ ≠
- 23. Статистика и критическая область Для проверки гипотезы используется t-критерий с df = n – 2 степенями
- 24. Пример Задача. Рассчитан коэффициент корреляции и его значение оказалось равно 0,897. Выборка содержала 6 пар. На
- 25. Решение Шаг 4. Сравниваем значение статистики с критической областью. Нулевую гипотезу отвергаем, так как значение критерия
- 26. Корреляция и причинная связь Когда проверка гипотезы показывает, что существует значимая линейная связь между переменными, исследователи
- 27. Пять видов связи между переменными 1. Прямая причинно-следственная связь между переменными (х определяет у). Наличие воды
- 28. * 12.3. Регрессия
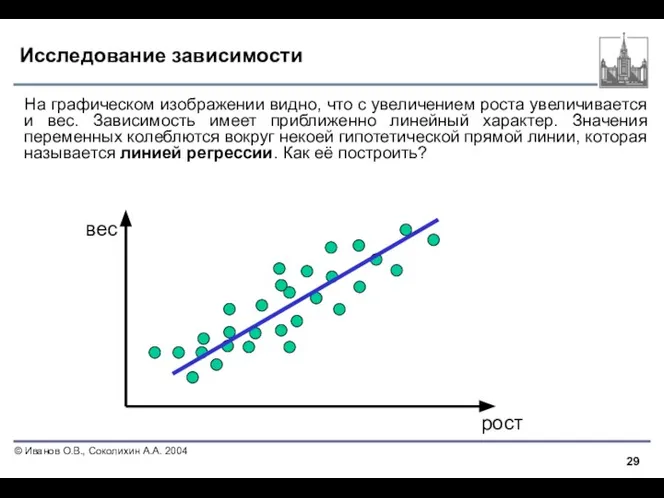
- 29. Исследование зависимости На графическом изображении видно, что с увеличением роста увеличивается и вес. Зависимость имеет приближенно
- 30. Какая прямая наилучшая? Наши данные представляют собой пары (x, y). Тем самым, для каждого x имеется
- 31. Сумма квадратов разностей минимальна… Расстояние между этими значениями должно быть минимально.
- 32. Ищем коэффициенты уравнения y = ax + b В каком случае расстояние минимально? Сумма зависит только
- 33. Коэффициенты a и b Два уравнения, которые мы получим после нахождения двух частных производных, представляют систему
- 34. Формулы для вычислений в таблице Для табличный вычислений более удобны следующие формулы:
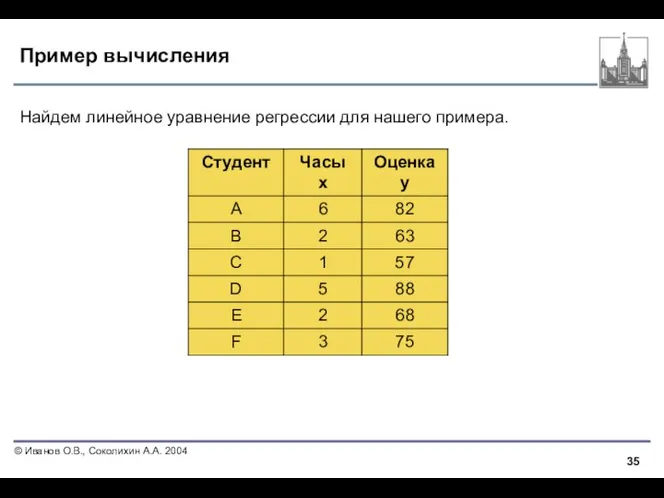
- 35. Пример вычисления Найдем линейное уравнение регрессии для нашего примера.
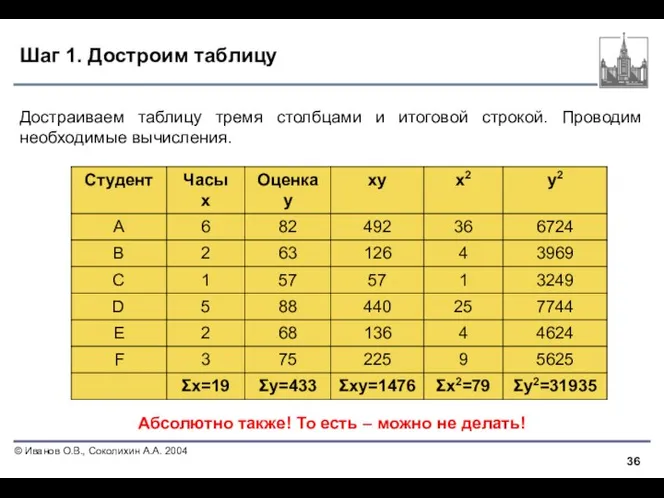
- 36. Шаг 1. Достроим таблицу Достраиваем таблицу тремя столбцами и итоговой строкой. Проводим необходимые вычисления. Абсолютно также!
- 37. Шаги 2-3. Подставим в формулы, получим ответ Подставим полученные в таблице значения в формулы для a
- 38. Интерпретация 1. Увеличение времени подготовки на 1 час приводит к улучшению результата на 5,6 балла. 2.
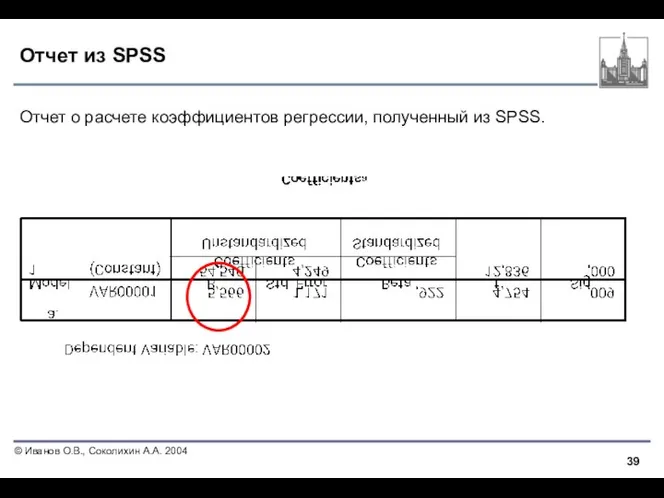
- 39. Отчет из SPSS Отчет о расчете коэффициентов регрессии, полученный из SPSS.
- 40. Будьте осторожны с прогнозами! Когда прогнозы распространяются за пределы исследуемых данных, интерпретировать результаты необходимо с особой
- 41. * 12.4. Надежность прогноза
- 42. Регрессионное исследование Уже научились: Шаг 1. Графически изобразить пары значений (x, y). Шаг 2. Если визуально
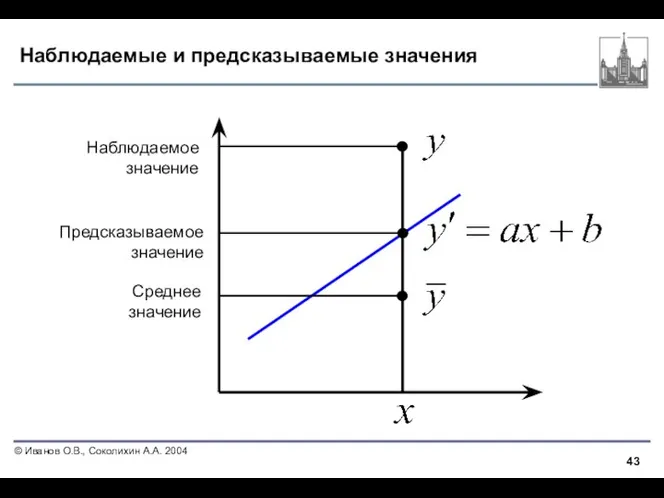
- 43. Наблюдаемые и предсказываемые значения Наблюдаемое значение Предсказываемое значение Среднее значение
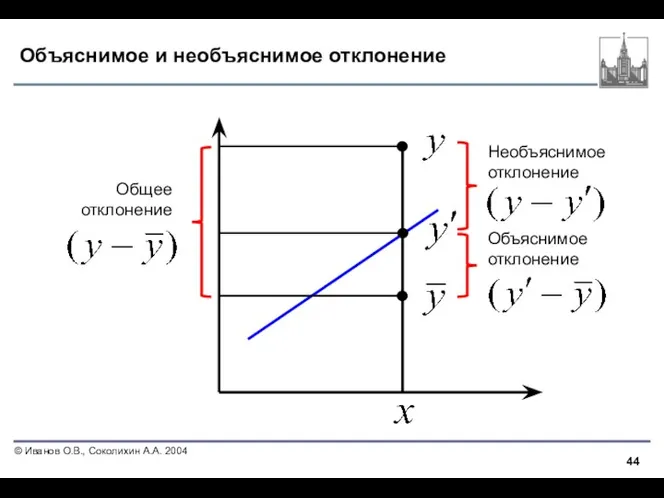
- 44. Объяснимое и необъяснимое отклонение Необъяснимое отклонение Объяснимое отклонение Общее отклонение
- 45. Вариация в регрессионной модели Общее отклонение есть сумма объяснимой и необъяснимой вариации: Общая вариация Объяснимая вариация
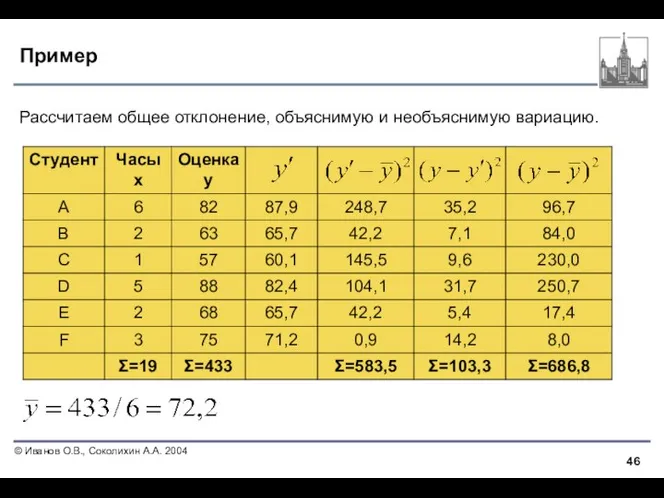
- 46. Пример Рассчитаем общее отклонение, объяснимую и необъяснимую вариацию.
- 47. Коэффициент детерминации Коэффициент детерминации вычисляется как отношение объяснимой вариации к общей вариации: Коэффициент детерминации – это
- 48. Пример Вычислим на основе результатов, полученных в таблице:
- 49. Интерпретация коэффициента детерминации Значение коэффициента детерминации можно получить, если возвести в квадрат коэффициент корреляции. Если r
- 50. Стандартная ошибка оценки Стандартная ошибка оценки – это стандартное отклонение наблюдаемых значений у от предсказываемых значений
- 51. Пример Рассчитаем стандартную ошибку оценки в нашем примере:
- 52. Вторая формула для стандартной ошибки Стандартную ошибку можно также вычислять по формуле: Эта формула более пригодна
- 53. Интервал предсказания Когда конкретное значение х подставляется в уравнение регрессии, мы получаем предсказанное значение у′, которое
- 54. Пример Сколько баллов получит студент, занимавшийся 4 часа? Решение. Шаг 1. Провели необходимые вычисления в таблице
- 55. Пример Шаг 6. Подставили в формулу интервала: Ответ. Прогнозируемое значение баллов, которое может получить студент при
- 56. Задание на 5 минут Можно ли при помощи χ2 критерия проверить гипотезу о том, является ли
- 57. Задачи 12-1. Исследователь хочет определить, существует ли связь между возрастом человека и тем, сколько часов в
- 58. Задачи 12-2. Президент ассоциации выпускников знаменитого колледжа хочет определить, есть ли какая либо взаимосвязь между размерами
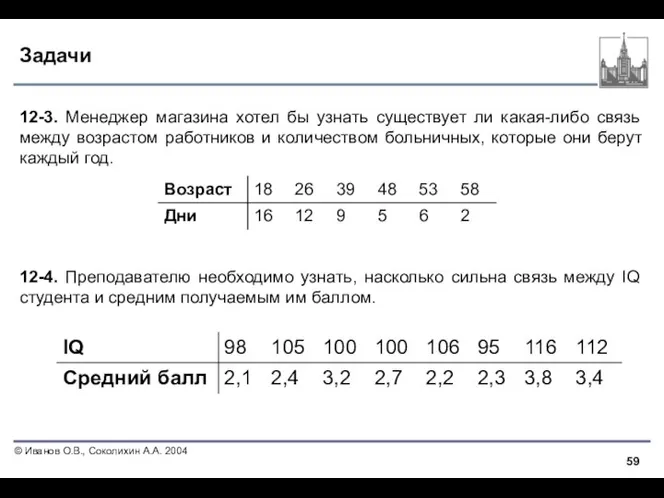
- 59. Задачи 12-3. Менеджер магазина хотел бы узнать существует ли какая-либо связь между возрастом работников и количеством
- 60. Задачи 12-5. Исследователь хочет определить, есть ли связь между тем, сколько лет уже прослужила копировальная машина,
- 61. Задачи 12-6. Вычислите значение r для следующих данных и проверьте гипотезу Н0: ρ = 0 Нарисуйте
- 62. Задачи В задачах 12-7 по 12-10 проведите регрессионный анализ: а) Нарисуйте график. б) Вычислите значение коэффициента
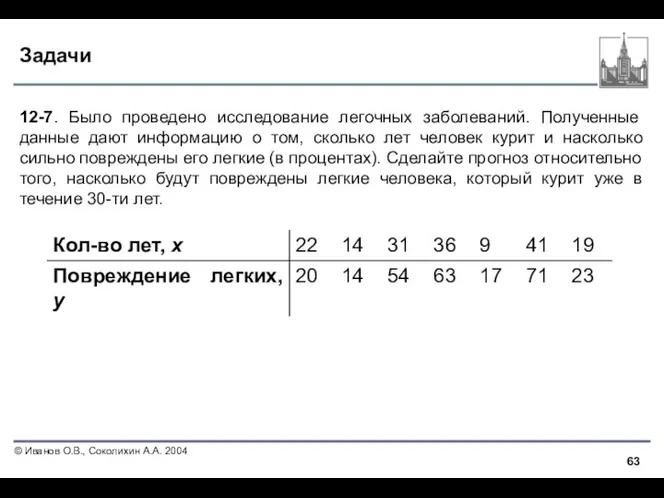
- 63. Задачи 12-7. Было проведено исследование легочных заболеваний. Полученные данные дают информацию о том, сколько лет человек
- 64. Задачи 12-8. Преподаватель статистики заинтересован в том, чтобы узнать силу связи между баллами, полученными на выпускных
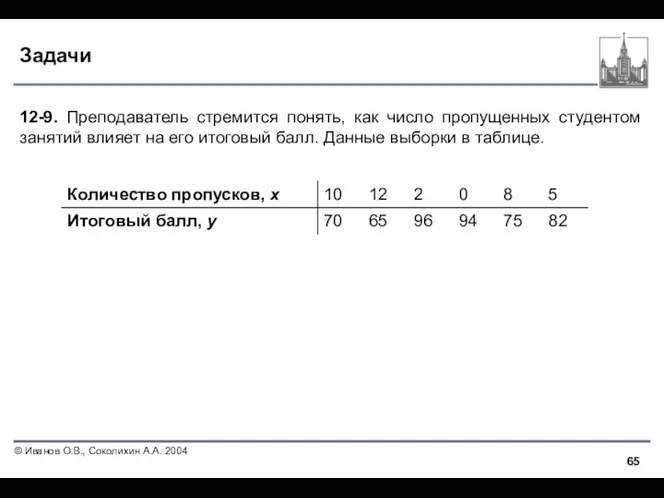
- 65. Задачи 12-9. Преподаватель стремится понять, как число пропущенных студентом занятий влияет на его итоговый балл. Данные
- 66. Задачи 12-10. Было проведено исследование, нацеленное на то чтобы выявить, как зависит от ежемесячного дохода человека
- 68. Скачать презентацию

















































 Презентация на тему Электролиты
Презентация на тему Электролиты Поздравляем вас, наши любимые мужчины!
Поздравляем вас, наши любимые мужчины! Баш3орт милли аштары
Баш3орт милли аштары История ислама
История ислама «Товаропроводящая цепочка фармацевтических препаратов. Где тонко, там и рвется (а где тонко?)».
«Товаропроводящая цепочка фармацевтических препаратов. Где тонко, там и рвется (а где тонко?)». Основные концепции культуры
Основные концепции культуры Декоративно- прикладное творчество народов Поволжья
Декоративно- прикладное творчество народов Поволжья Синхронный электродвигатель
Синхронный электродвигатель Мероприятия по энергосбережению в электрических сетях электроосвещения объектов капитального строительства
Мероприятия по энергосбережению в электрических сетях электроосвещения объектов капитального строительства КОНСТРУИРОВАНИЕ
КОНСТРУИРОВАНИЕ Зона смешанных и широколиственных лесов 8 класс
Зона смешанных и широколиственных лесов 8 класс Выставка марийских национальных костюмов
Выставка марийских национальных костюмов Особенности празднования Нового года в России
Особенности празднования Нового года в России Детская площадка
Детская площадка The system of State bodies of India
The system of State bodies of India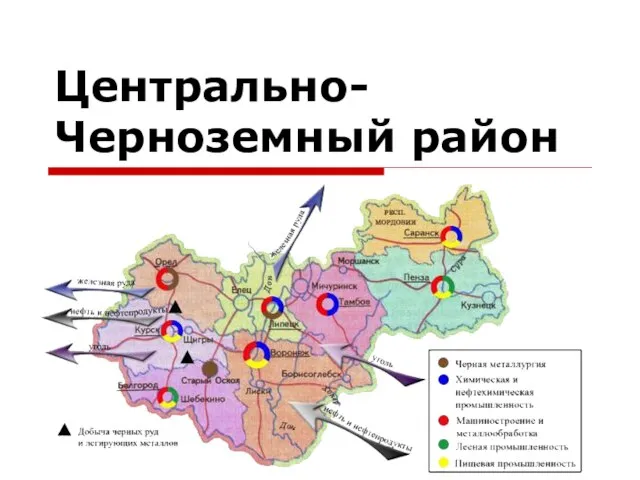 Центрально-Черноземный район
Центрально-Черноземный район Повторение. Чтение текста с изученными буквами
Повторение. Чтение текста с изученными буквами Конституционное право. Своя игра
Конституционное право. Своя игра Холодная прокатка труб (ХПТ).Краснов Денис
Холодная прокатка труб (ХПТ).Краснов Денис От кого же, мы всё же произошли?
От кого же, мы всё же произошли? Презентация_32
Презентация_32 Государственное общеобразовательное учреждение средняя общеобразовательная школа № 28 Василеостровского района
Государственное общеобразовательное учреждение средняя общеобразовательная школа № 28 Василеостровского района Туесок из стружки с геометрической резьбой
Туесок из стружки с геометрической резьбой Бизнес Мечты!
Бизнес Мечты! Typológia 3 - Letiská
Typológia 3 - Letiská Готовимся к
Готовимся к Апельсиновое настроение. Рисуем апельсины. Декоративный натюрморт в технике масляной живописи
Апельсиновое настроение. Рисуем апельсины. Декоративный натюрморт в технике масляной живописи Выпуск Эльгяйской СОШ 1972 года
Выпуск Эльгяйской СОШ 1972 года