Общие теоремы динамики

Цель урока:
Обеспечение усвоения понятий импульса силы, количества движения, кинетической энергии, механической системы, внутренних и внешних сил системы.
Способствовать формированию представлений об основных уравнениях динамики.
Способствовать формированию умений определять параметры движения с помощью теорем динамики.

Любое взаимодействие тел, приводящее к какому-либо изменению движения, длится в течение некоторого времени.
Векторная мера действия силы Fdt, равная произведению силы на элементарный промежуток времени ее действия, называется элементарным импульсом силы.
Направление вектора импульса совпадает с направлением вектора силы.
Единица импульса в СИ — Н·с:
1 Н · с = 1 кг · м/с2 · 1 с = 1 кг · м/с
При F= const импульс силы за время Δt=t2—t1 равен
F Δt

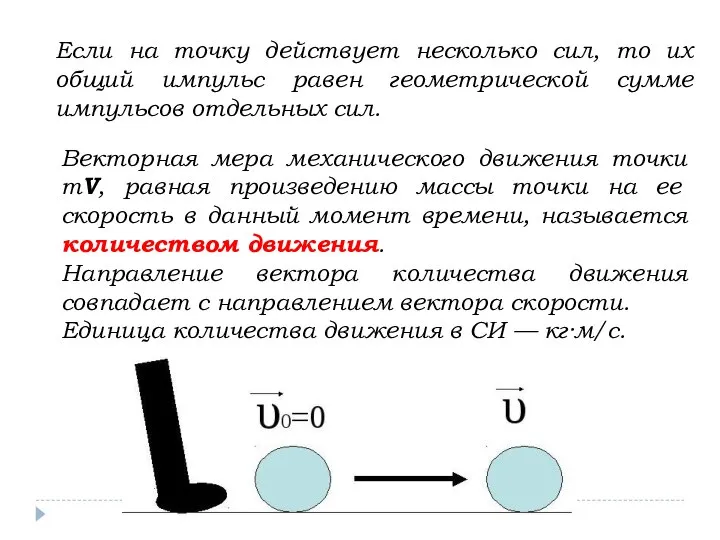
Если на точку действует несколько сил, то их общий импульс равен геометрической сумме импульсов отдельных сил.
Векторная мера механического движения точки mV, равная произведению массы точки на ее скорость в данный момент времени, называется количеством движения.
Направление вектора количества движения совпадает с направлением вектора скорости.
Единица количества движения в СИ — кг·м/с.

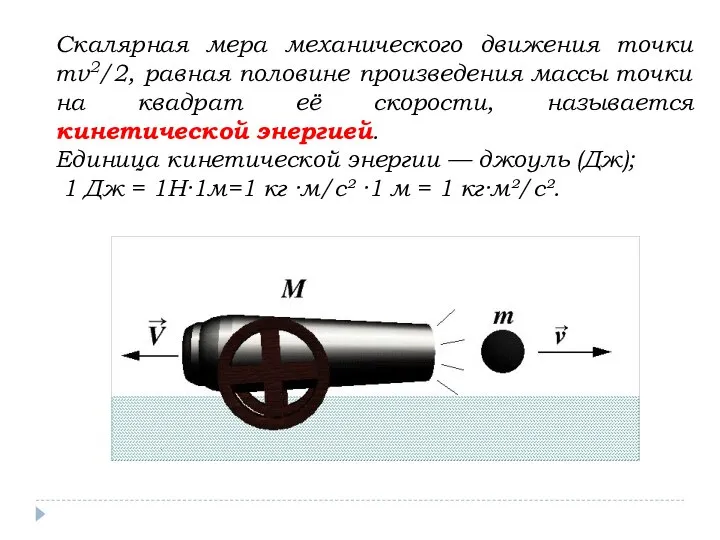
Скалярная мера механического движения точки mv2/2, равная половине произведения массы точки на квадрат её скорости, называется кинетической энергией.
Единица кинетической энергии — джоуль (Дж);
1 Дж = 1Н·1м=1 кг ·м/с² ·1 м = 1 кг·м²/с².

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
Пусть на точку массой m действует система постоянных сил, равнодействующая которых FΣ.
Согласно основному закону динамики:
FΣ = та
Учитывая время действия сил, умножим обе части равенства на продолжительность их действия Δt:
FΣ Δt = та Δt
a = (V2—V1)/(Δt)

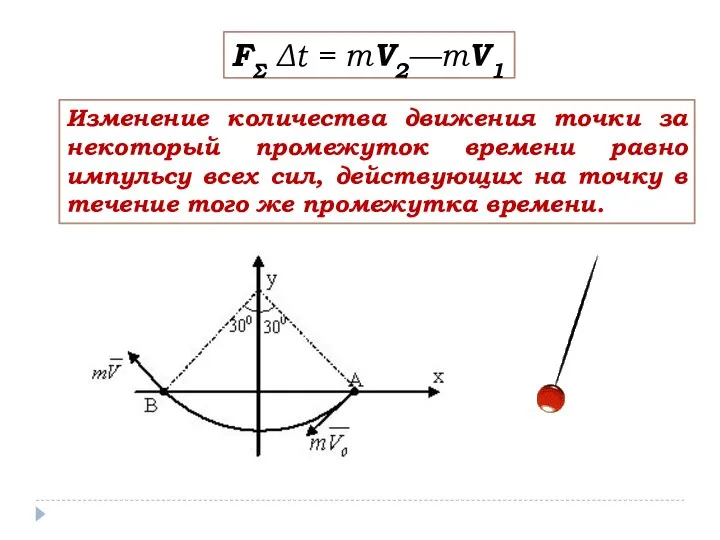
FΣ Δt = mV2—mV1
Изменение количества движения точки за некоторый промежуток времени равно импульсу всех сил, действующих на точку в течение того же промежутка времени.

Пример1. Шофер автомобиля, движущегося со скоростью 60 км/ч, выключил двигатель и начал торможение. Через сколько времени автомобиль остановится, если сила торможения составляет 0,8 от силы тяжести автомобиля?
Решение.
Приняв автомобиль за материальную точку, отметим буквой А место начала торможения (скорость автомобиля V1=60км/ч=16,7м/с), а буквой В—место остановки автомобиля (V2=0).
При движении автомобиля между точками А и В в течение Δt на него действует тормозящая сила Fтр = Rf , равная Rf =0,8 G=0,8 mg.

Rf Δt = —mV1
Спроецировав обе части равенства на ось, проходящую через точки А и В, получим:
— Rf Δt =— mV1
Δt=mV1/Rf=mV1/(0,8mg)=16,7/(0,8·9,8)= = 2,13 с
Автомобиль остановится через 2,13 с.

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
Пусть, как и в предыдущем случае, на точку действует система постоянных сил, равнодействующая которых FΣ, и ради упрощения рассуждений допустим, что силы действуют вдоль одной прямой.
Тогда основному закону динамики в векторной форме эквивалентно равенство:
FΣ = та
Умножим обе части этого равенства на перемещение точки ΔS:
FΣ ΔS = ma ΔS

При действии постоянных сил на прямолинейном пути:
a = (V2— V1)/Δt
ΔS = Vср Δt = (V2 + V1) Δt/2
FΣ ΔS = m[(V2— V1)/Δt][(V2 + V1)/Δt]/2
FΣ ΔS = WΣ = ΣWk
ΣWk = mV²2/2 — mV²1/2
Изменение кинетической энергии точки на некотором пути равно сумме работ всех действующих на точку сил на том же пути.

Если точка движется равномерно, т. е. V1=V2, и изменение кинетической энергии mV²2/2—mV²1/2=0, то
ΣWk =0
Если V1>V2, то изменение кинетической энергии mV²2/2—mV²1/2>0, т. е. кинетическая энергия точки возрастает и, значит, работа движущих сил больше работ сил сопротивления.
Если V1

Пример 2. По условию примера 1 определить длину тормозного пути AB=S автомобиля.
Решение.
В соответствии с исходными данными уравнение кинетической энергии примет вид:
— Rf S = — mV²2/2
Отсюда, имея в виду, что Rf =0,8 mg, получим
S=mV²2/(2·0,8mg)=16,72/(2·0,8·9,8)≈17м
Тормозной путь составит 17 м.

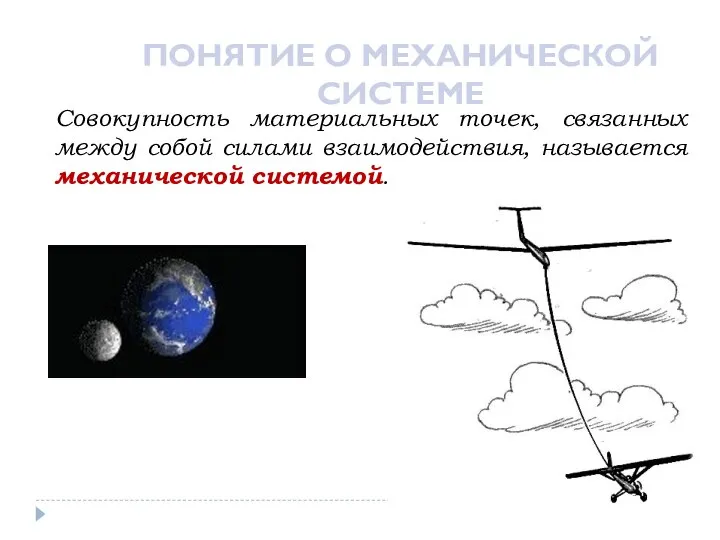
ПОНЯТИЕ О МЕХАНИЧЕСКОЙ СИСТЕМЕ
Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.

Любое материальное тело рассматривается в механике как механическая система, образуемая совокупностью материальных точек.
Абсолютно твердое тело называется неизменяемой механической системой, так как расстояние между материальными точками остается неизменным.
Механические системы, расстояния между точками которых могут меняться, называются изменяемыми. К ним относятся любые машины или механизмы.

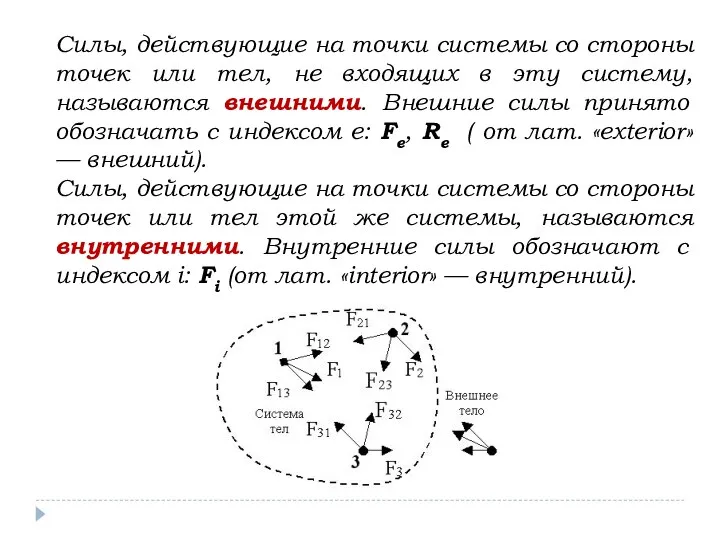
Силы, действующие на точки системы со стороны точек или тел, не входящих в эту систему, называются внешними. Внешние силы принято обозначать с индексом е: Fe, Re ( от лат. «exterior» — внешний).
Силы, действующие на точки системы со стороны точек или тел этой же системы, называются внутренними. Внутренние силы обозначают с индексом i: Fi (от лат. «interior» — внутренний).

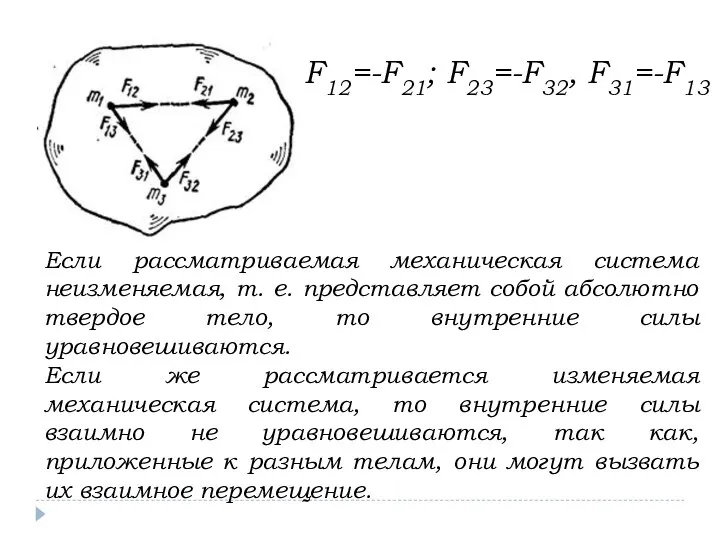
F12=-F21; F23=-F32, F31=-F13
Если рассматриваемая механическая система неизменяемая, т. е. представляет собой абсолютно твердое тело, то внутренние силы уравновешиваются.
Если же рассматривается изменяемая механическая система, то внутренние силы взаимно не уравновешиваются, так как, приложенные к разным телам, они могут вызвать их взаимное перемещение.