Содержание
- 2. Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил
- 3. Фракталы получают с помощью некоторой ломаной. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется
- 4. Рассмотрим одну из таких фрактальных кривых - кривую Коха. Построение кривой начинается с отрезка единичной длины
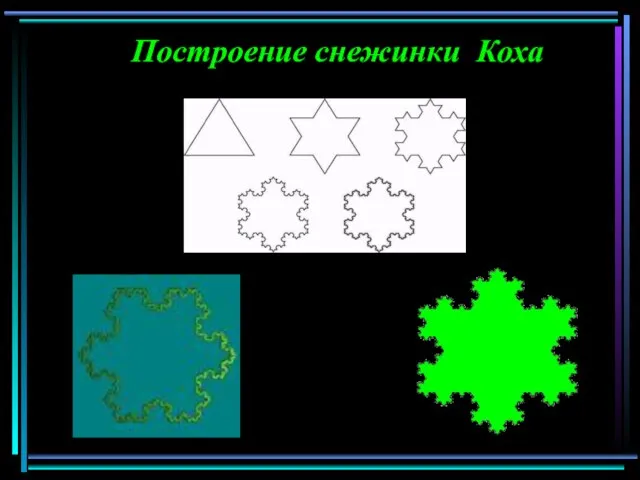
- 5. Построение снежинки Коха
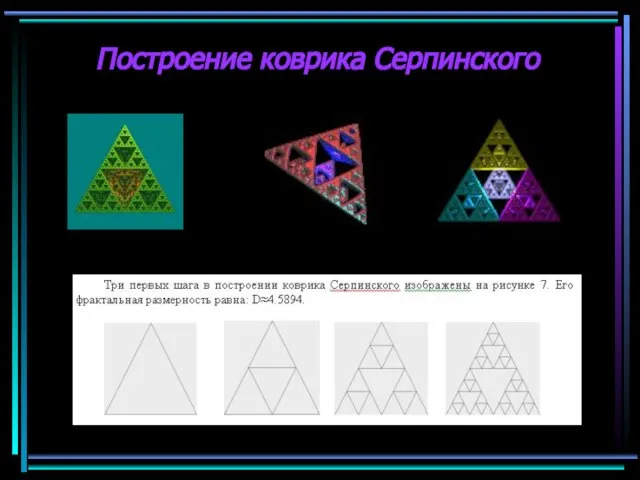
- 6. Построение коврика Серпинского
- 7. Мы привыкли изображать объекты окружающего нас мира как сплошные тела с четко обозначенными границами. Но далеко
- 8. Когда-то создание правдоподобного пейзажа с помощью компьютера было чрезвычайно трудным делом. Но, начиная с 1980г., все
- 9. Бенуа Мандельброт родился в Варшаве в 1924 году. Окончил Парижский университет Сорбонну. Работает в области экономики,
- 10. Парадоксальная сущность природы фракталов состоит в том, что, благодаря своему бесконечно сложному строению фрактальные "кружева" имеют
- 11. Характерным свойством множеств Мандельброта и Жюлиа является самоподобие их отдельных деталей на разных масштабных уровнях рассмотрения.
- 12. Фрактальные деревья
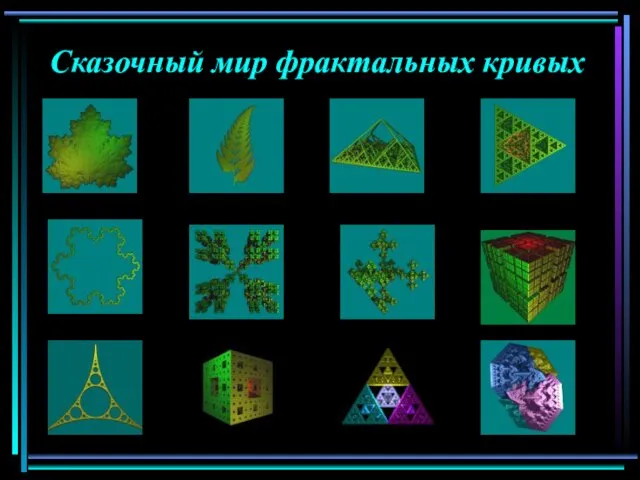
- 13. Сказочный мир фрактальных кривых
- 14. Сказочный мир фрактальных кривых
- 15. Сказочный мир фрактальных кривых
- 16. Кубик Серпинского, известный также как губка Менгера. Состоит из двадцати точно таких же кубиков, только маленьких,
- 17. Гармония рождается из хаоса
- 20. Скачать презентацию














 Новый менеджер в сформировавшейся команде – методы безболезненного внедрения Вершинина Екатерина
Новый менеджер в сформировавшейся команде – методы безболезненного внедрения Вершинина Екатерина SPE Outstanding Student Chapter and Gold Award Criteria
SPE Outstanding Student Chapter and Gold Award Criteria Предлог
Предлог Презентация на тему Физминутка для глаз
Презентация на тему Физминутка для глаз  Теплота згоряння палива. Розрахунок кількості теплоти внаслідок згоряння палива
Теплота згоряння палива. Розрахунок кількості теплоти внаслідок згоряння палива Вакцины от ВПЧ. Конкурентная борьба и стратегия работы врача женской консультации.Нужна ли нам государственная программа вакцина
Вакцины от ВПЧ. Конкурентная борьба и стратегия работы врача женской консультации.Нужна ли нам государственная программа вакцина Египетские пирамиды в Гизе
Египетские пирамиды в Гизе О дисциплинах цикла ГСЭ
О дисциплинах цикла ГСЭ Проект для сотрудников (шаблон)
Проект для сотрудников (шаблон) «Работа учреждения в рамках реализации закона 83-ФЗ»
«Работа учреждения в рамках реализации закона 83-ФЗ» Карикатурный портрет
Карикатурный портрет Am, is or are
Am, is or are ДОКЛАД: М.М. ТУЛЯГАНОВОЙ ОСОБЕННОСТИ НЕФОРМАЛЬНОЙ ЭКОНОМИКИ В РЕСПУБЛИКЕ УЗБЕКИСТАН
ДОКЛАД: М.М. ТУЛЯГАНОВОЙ ОСОБЕННОСТИ НЕФОРМАЛЬНОЙ ЭКОНОМИКИ В РЕСПУБЛИКЕ УЗБЕКИСТАН Кленовый лист, кленовый лист, ты мне среди зимы приснись
Кленовый лист, кленовый лист, ты мне среди зимы приснись Путешествия в сказку
Путешествия в сказку Визитная карточка школы
Визитная карточка школы ОПЕРАТИВНАЯ ПОЛИГРАФИЯ
ОПЕРАТИВНАЯ ПОЛИГРАФИЯ Учебный проектОсновные темы рассказа А.И. Куприна «Белый пудель»
Учебный проектОсновные темы рассказа А.И. Куприна «Белый пудель» London. Sightseeing of London
London. Sightseeing of London Документы и сведения, представляемые таможенным органам при прибытии на таможенную территорию Подготовили: студентки 3-го курса
Документы и сведения, представляемые таможенным органам при прибытии на таможенную территорию Подготовили: студентки 3-го курса  Логічні одиниці інформаціи
Логічні одиниці інформаціи Основы ЭКГ
Основы ЭКГ Английская монархия от завоевания до парламента
Английская монархия от завоевания до парламента Налоги. Объект налогообложения
Налоги. Объект налогообложения Освещение. Свет и тень. Правила распределения светотени в натюрморте
Освещение. Свет и тень. Правила распределения светотени в натюрморте Презентация "Художественный образ в произведениях музыки и изобразительного искусства" - скачать презентации по МХК
Презентация "Художественный образ в произведениях музыки и изобразительного искусства" - скачать презентации по МХК Учитель начальных классов высшей категории МОУ «СОШ №6» г. Бузулука Оренбургской области
Учитель начальных классов высшей категории МОУ «СОШ №6» г. Бузулука Оренбургской области Организация и планирование закупок. Тема 2
Организация и планирование закупок. Тема 2