Кривые и поверхности высших порядков

Кривые высших порядков: постановка задачи
Задача: построить параметрическую кривую “повторяющую” заданную ломаную (на плоскости или в пространстве)
- контрольные точки
Для рисования кривая обычно разбивается на M точек
- базисные функции (обычно полиномы некоторой степени)

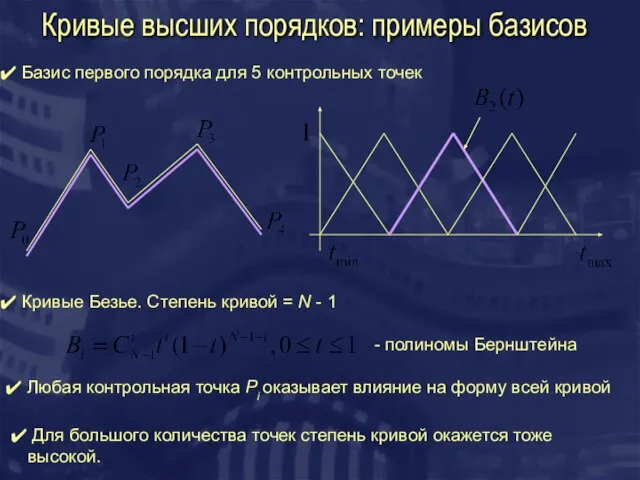
Кривые высших порядков: примеры базисов
Базис первого порядка для 5 контрольных точек Кривые Безье. Степень кривой = N - 1
Любая контрольная точка Pi оказывает влияние на форму всей кривой
Для большого количества точек степень кривой окажется тоже высокой.
- полиномы Бернштейна

Кривые высших порядков: B-сплайны
Задача: построить параметрическую кривую, форма которой изменяется локально при изменении одной из контрольных точек.
Базисные функции рассчитываются по рекуррентным формулам Кокса-де Бура.
p - степень B-сплайна.

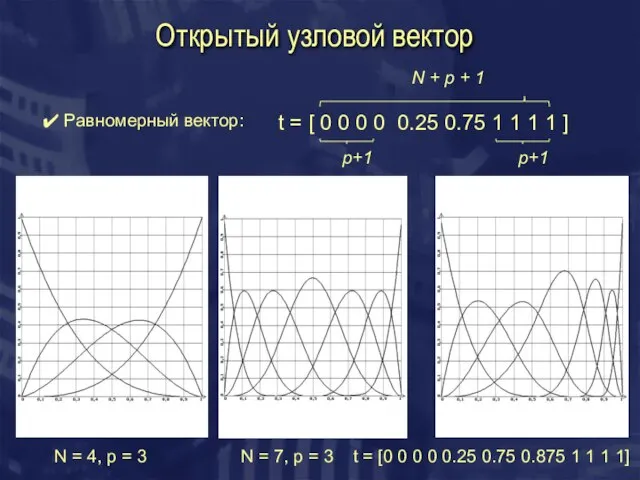
Открытый узловой вектор
Равномерный вектор:
t = [ 0 0 0 0 0.25 0.75 1 1 1 1 ]
p+1
p+1
N + p + 1
N = 4, p = 3
N = 7, p = 3
t = [0 0 0 0 0.25 0.75 0.875 1 1 1 1]

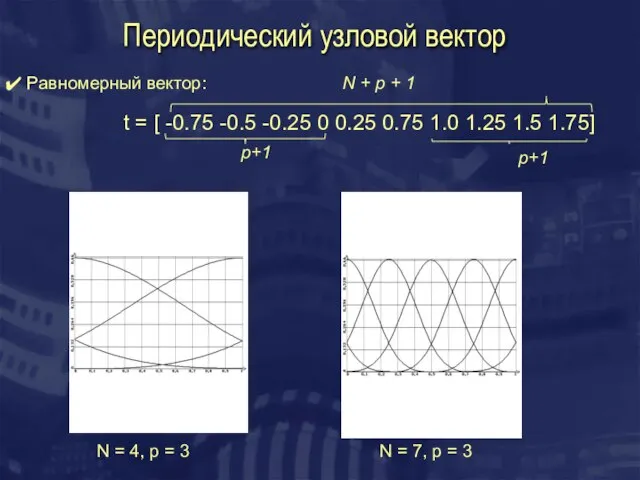
Периодический узловой вектор
Равномерный вектор:
t = [ -0.75 -0.5 -0.25 0 0.25 0.75 1.0 1.25 1.5 1.75]
p+1
p+1
N + p + 1
N = 4, p = 3
N = 7, p = 3

Повторяющиеся узлы
t = [ 0 0 0 0 0.5 0.5 0.5 1 1 1 1 ]
N = 7, p = 3

Расчет производных
Коэффициенты при степенях постоянны на каждом из интервалов узлового вектора: Формулы для вычисления получаются из формул Кокса-де-Бура

Рациональные сплайны
Рациональный сплайн является проекцией обычного сплайна из пространства более высокой размерности (см. однородные координаты)
w > 0 является веcом вершины. Чем больше вес, тем большее влияние вершина оказывает на форму кривой.
Формулы для пересчета нормалей оказываются неверными.

B-Spline поверхности
Поверхность строится на основе двух наборов базисных функций
Край поверхности является В-сплайном, который определяют граничные контрольные точки (для открытого базиса)

Литература
Роджерс Д., Адамc Дж. Математические основы машинной графики.
vprat. ifrance.com - статься про NURBS
Копия этой статьи на сайте cg.cs.msu.su
www.google.com :)

Вспомогательная библиотека GLU
Входит в состав OpenGL и основана на командах OpenGL Функции GLU можно разделить на четыре класса
Вспомогательные функции (gluPerspective, gluLookAt, …)
Функции для рисования базовых геометрических объектов: сферы, цилиндра, круга и сектора круга.
Функции для разбиения невыпуклых многоугольников
Функции для работы с кривыми и поверхностями NURBS

Рисование геометрических объектов (1/2)
Перед началом рисования необходимо создать объект GLUQuadricObj, хранящий режимы рисования объектов GLU
GLUquadricObj *obj = gluNewQuadric();
Для управления режимами рисования предназначены следующие функции:
gluQuadricDrawStyle Каркасный или сплошной режим рисования
gluQuadricOrientation Направление нормалей
gluQuadricNormals Режим расчета нормалей
gluQuadricTexture Рассчитывать или нет текстурные координаты
gluQuadricNormals(obj, GL_FLAT);

Рисование геометрических объектов (2/2)
disk
partial disk
sphere
Для рисования объектов предназначены функции gluSphere, gluCylinder, gluDisk и gluPartialDisk.
gluSphere(obj, 1.0, 20, 10);
Когда объект не нужен, память можно освободить
gluDeleteQuadric(obj);

Рисование кривых и поверхностей NURBS (1/2)
Перед началом рисования кривой или поверхности NURBS необходимо создать объект для хранения режимов построения NURBS
GLUnurbsObj *obj = new gluNewNurbsRenderer();
При помощи функции gluNurbsProperty можно задать режим разбиения, режим рисования и режимы отсечения кривых и поверхностей.
Предусмотрены следующие режимы разбиения кривых и поверхностей:
1. Постоянный шаг по параметрам u и v
2. Адаптивное разбиение в зависимости от длины кривой/площади поверхности на экране.
3. Адаптивное разбиение в зависимости от ошибки аппроксимации

Рисование кривых и поверхностей NURBS (2/2)
Рисование кривой NURBS
Между командами gluBeginCurve и gluEndCurve вызываются команды gluNurbsCurve для задания массивов контрольных точек, а также нормалей, цветов и текстурных координат вершин.
Рисование поверхности NURBS
Между командами gluBeginSurface и gluEndSurface вызываются команды gluNurbsSurface для задания массивов контрольных точек, а также нормалей, цветов и текстурных координат вершин.

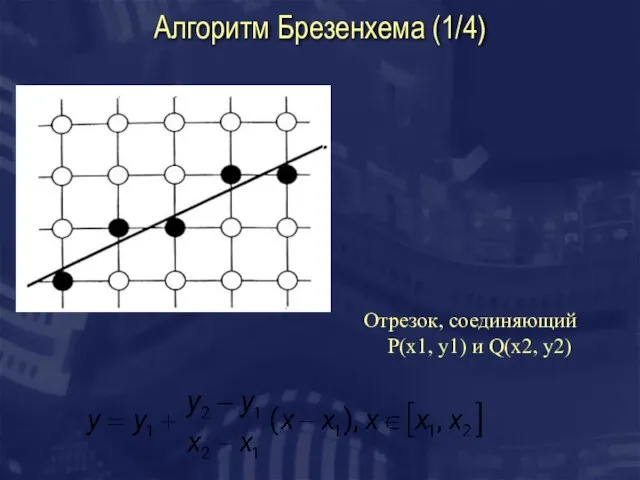
Алгоритм Брезенхема (1/4)
Отрезок, соединяющий P(x1, y1) и Q(x2, y2)

Алгоритм Брезенхема (2/4)
F(x,y) = 0 -- точка на отрезке
F(x,y) < 0 -- точка выше
F(x,y) > 0 -- точка ниже
Точка P определена, тогда координаты срединной точки
и значение функции в этой точке

Алгоритм Брезенхема (3/4)
Если d < 0, то выбирается Е и
Если d ≥ 0, то выбирается NE
В начальной точке

Алгоритм Брезенхема (4/4)
Одна неприятность -- деление на 2
Чтобы избежать вещественной арифметики, сделаем преобразование
d0 = 10 - 7 = 3 > 0 (NE)
d1 = 3 - 4 = -1 < 0 (E)
d2 = -1 + 10 = 9 (NE)
d3 = 9 - 4 = 5 (NE)
d4 = 5 - 4 = 1 (NE)
d5 = 1 - 4 = -3 (E)
d6 = -3 + 10 = 7 (NE)

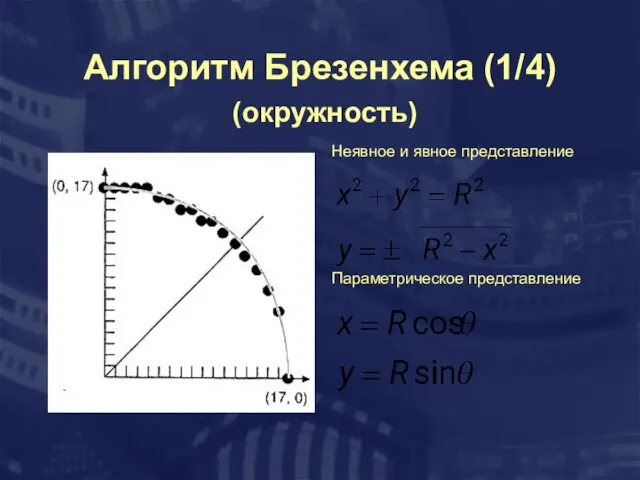
Алгоритм Брезенхема (1/4)
(окружность)
Неявное и явное представление
Параметрическое представление

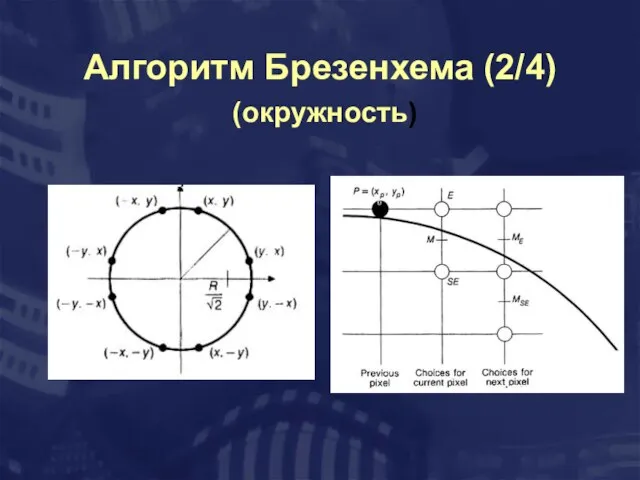
Алгоритм Брезенхема (2/4)
(окружность)

Алгоритм Брезенхема (3/4)
(окружность)
Для точки P c коорд.
Для пиксела Е:
Для пиксела SE: