Слайд 2Общее значение.
Аксиомами называются утверждения, содержащиеся в формулировках основных свойств простейших фигур. Слово

«аксиома» происходит от греческого слова «аксиос» и означает «утверждение, не вызывающее сомнений».
Слайд 3Аксиома №1
Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и

точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Слайд 4Пример к аксиоме №1
Задание: Могут ли две прямые иметь две точки пересечения?
Решение:

Если бы две прямые имели две точки пересечения, то через эти точки проходили бы две прямые. А это невозможно, т.к. через две точки можно провести только одну прямую.
Ответ: две прямые не могут иметь две точки пересечения.
Слайд 5Аксиома №2
Из трех точек на прямой одна и только одна лежит между

двумя другими.
Слайд 6Аксиома №3
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме

длин частей, на которые он разбивается любой его точкой.
Слайд 7Пример к аксиоме №3
Дано: три точки A, B, C лежат на одной

прямой. Известно, что AB=4,3 см, AC=7,5 см, BC=3,2 см.
Найти: Какая из трех точек A,B,C лежит между двумя другими?
Решение: например возьмем точку В. Если точка В лежит между точками А и С, то по аксиоме №3 должно быть АВ+ВС=АС. Тогда 4,3+3,2=7,5. Значит, точка В - правильный ответ.
Ответ: точка В лежит между точками А и С.
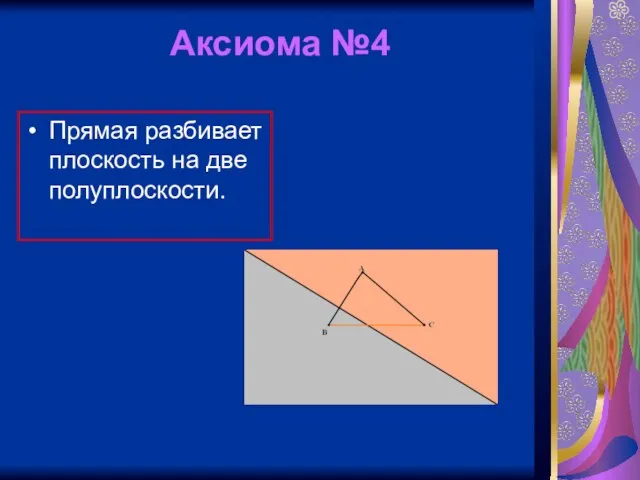
Слайд 8Аксиома №4
Прямая разбивает плоскость на две полуплоскости.
Слайд 9Аксиома №5
Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен

180 градусам. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Слайд 10Пример к аксиоме №5
Найти: Может ли луч с проходить между сторонами угла

(аb), если угол (ac)=30 градусам, угол (сb)=80 градусам, угол (аb)=50 градусам?
Решение: Если луч с проходит между сторонами угла (аb), то по аксиоме №5 должно быть – угол (ас)+ угол (bс) = углу (аb). Но 30гр.+80гр. не равно 50 гр. Значит, луч с не может проходить между сторонами угла (ab).
Ответ: луч с не может проходить между сторонами угла(аb).
Слайд 11Аксиома №6 и аксиома №7
А №6 На любой полупрямой от ее начальной

точки можно отложить отрезок заданной длины, и только один.
А №7 От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 гр., и только один.
Слайд 12Пример к аксиомам №6 и №7
Дано: На луче АВ отложен отрезок АС,

меньший отрезка АВ.
Найти: Какая из трех точек А, В, С лежит между двумя другими? Ответ объяснить.
Решение: Так как точки В и С лежат на одной полупрямой с начальной точкой А, то они не разделяются точкой А, т.е. точка А не лежит между точками В и С.
Если бы точка В лежала между точками А и С, то было бы АВ+ВС=АС. Но это невозможно, так как по условию отрезок АС меньше отрезка АВ. Значит, точка В не лежит между точками А и С. Тогда точка С - правильный ответ.
Ответ: точка С лежит между точками А и В.
Слайд 13Аксиома №8
Каков бы ни был треугольник, существует равный ему треугольник в заданном

расположении относительно данной полупрямой.
Слайд 14Аксиома №9
Через точку, не лежащую на данной прямой, можно провести на плоскости

не более одной прямой, параллельной данной.
Слайд 15Пример к аксиоме №9
Задание: Может ли прямая, пересекающая одну из двух параллельных

прямых, не пересекать другую? Ответ объяснить.
Решение: Пусть a и b – параллельные прямые, и пусть прямая c пересекает прямую а в точке А (см.рис.). Если бы прямая с не пересекала прямую b, то через точку А проходили бы две прямые, не пересекающие прямую b: прямая а и прямая с.Но по аксиоме №9 это невозможно. Значит, прямая с, пересекая прямую а, должна пересекать и параллельную ей прямую b.
Ответ: Прямая, пересекающая дну из двух параллельных прямых, пересекает прямую.














 Публичный отчет
Публичный отчет Два положения 2-го закона термодинамики. Круговые процессы тепловых машин. 2. Термический КПД цикла. Холодильный коэффициент. 3. Прям
Два положения 2-го закона термодинамики. Круговые процессы тепловых машин. 2. Термический КПД цикла. Холодильный коэффициент. 3. Прям Мы помним
Мы помним Эмиграционные настроения: портрет потенциального эмигранта
Эмиграционные настроения: портрет потенциального эмигранта 85689
85689 Об итогах социально-экономического развития Красновишерского муниципального района Пермского края за 2010 г. и о перспективах разв
Об итогах социально-экономического развития Красновишерского муниципального района Пермского края за 2010 г. и о перспективах разв Право в системе социальных норм
Право в системе социальных норм Презентация на тему Ядовитые грибы
Презентация на тему Ядовитые грибы Лидерство в системе менеджмента.Тесты
Лидерство в системе менеджмента.Тесты ПРЕДЕЛЫ МИРОВОГО ЭКОНОМИЧЕСКОГО РОСТА И ПОТРЕБЛЕНИЯ
ПРЕДЕЛЫ МИРОВОГО ЭКОНОМИЧЕСКОГО РОСТА И ПОТРЕБЛЕНИЯ Презентация на тему Чудотворные иконы России
Презентация на тему Чудотворные иконы России РАЗРАБОТКА И ВНЕДРЕНИЕ АВТОМАТИЗИРОВАННОЙ СИСТЕМЫ АНАЛИЗА И ПРОГНОЗИРОВАНИЯ ПРОИЗВОДСТВЕННЫХ СИТУАЦИЙ ДОМЕННОГО ЦЕХА С ЦЕЛЬЮ ПО
РАЗРАБОТКА И ВНЕДРЕНИЕ АВТОМАТИЗИРОВАННОЙ СИСТЕМЫ АНАЛИЗА И ПРОГНОЗИРОВАНИЯ ПРОИЗВОДСТВЕННЫХ СИТУАЦИЙ ДОМЕННОГО ЦЕХА С ЦЕЛЬЮ ПО Дисциплина: Международные перевозки грузов Раздел 1. Основы организации международной перевозки грузов Тема 1.2. Логистические си
Дисциплина: Международные перевозки грузов Раздел 1. Основы организации международной перевозки грузов Тема 1.2. Логистические си Альтернатива. Мозговая атака. Метод выдвижения предложений. Групповой анализ ситуации
Альтернатива. Мозговая атака. Метод выдвижения предложений. Групповой анализ ситуации История шоколада
История шоколада Обеспечение покрытия рисков при наступлении несчастного случая или укусе клеща во время нахождении детей в летних лагерях
Обеспечение покрытия рисков при наступлении несчастного случая или укусе клеща во время нахождении детей в летних лагерях FutureToday
FutureToday Природа и архитектура. Организация архитектурно-ландшафтного пространства
Природа и архитектура. Организация архитектурно-ландшафтного пространства Подготовка к ВПР
Подготовка к ВПР Гимназия №8
Гимназия №8 Я – Успешный человек?
Я – Успешный человек? Методические рекомендации к преподаванию модуля Основы православной культуры в курсе «Основы религиозных культур и светской эти
Методические рекомендации к преподаванию модуля Основы православной культуры в курсе «Основы религиозных культур и светской эти Инновационный поиск учителя
Инновационный поиск учителя Презентация 18.10
Презентация 18.10 Цель кодирования
Цель кодирования Презентация на тему Электронные деньги
Презентация на тему Электронные деньги  Взаимодействие с правоохранительными органами по вопросам борьбы с подделкой
Взаимодействие с правоохранительными органами по вопросам борьбы с подделкой Презентация на тему Храм святой Софии в Стамбуле
Презентация на тему Храм святой Софии в Стамбуле