Содержание
- 2. Типы алгоритмов. История создания Интенсивный поиск универсального уточнения алгоритма предложил примерно 20 формальных конструкций алгоритмов, которые
- 3. Алгоритмические машины (АМ) имеют единственный процессор, выполняющий небольшой набор очень примитивных действий, простую структуру данных (структуру
- 4. Основные АМ Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г. Машина Поста (МР) предложена Постом в
- 5. Функции вычислимые алгоритмом алгоритм не определяется формально, а существует как бы в виде «всем понятной механической
- 6. Рекурсивные функции на множестве натуральных чисел были предложены Клини в 1938 г. Конструктивные механизмы рекурсивных функций
- 7. Исчисления. Исчисление функций, вычисляемых на множестве натуральных чисел предложено Эрбраном и Гёделем в 1938 г. λ-исчисление
- 8. Структура алгоритма (составляющие алгоритма) Процессорная структура. (Исполнитель алгоритма). Во всех теоретических конструкциях алгоритмов и большинстве алгоритмических
- 9. Информационная структура алгоритма (ИСА). Структура функций есть описание конструирования функции от функций из базовых. Логическая структура
- 10. Интерпретация МТ. Процессор – в МТ называется управляющей головкой (УГ). Структура данных (память процессора) бесконечная лента,
- 11. ТЬЮРИНГ Алан Матисон (Turing Alan Mathison) (1912—1954), английский математик. Основные труды по математической логике, вычислительной математике.
- 12. МТ Тьюринг назвал свое абстрактное механическое устройство "универсальной машиной", поскольку она должна была справляться с любой
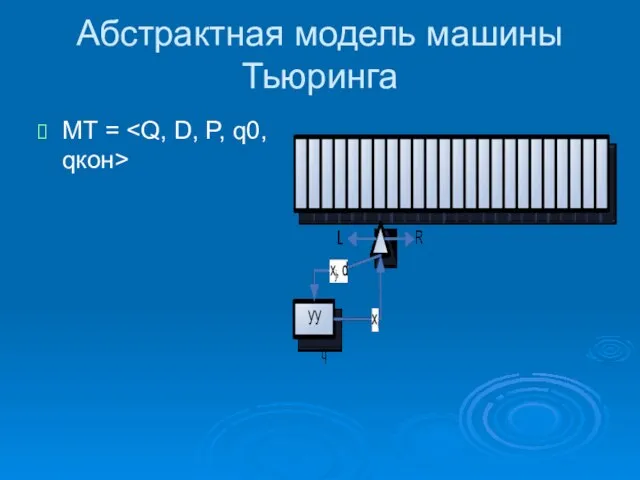
- 13. Абстрактная модель машины Тьюринга МТ =
- 14. МТ =
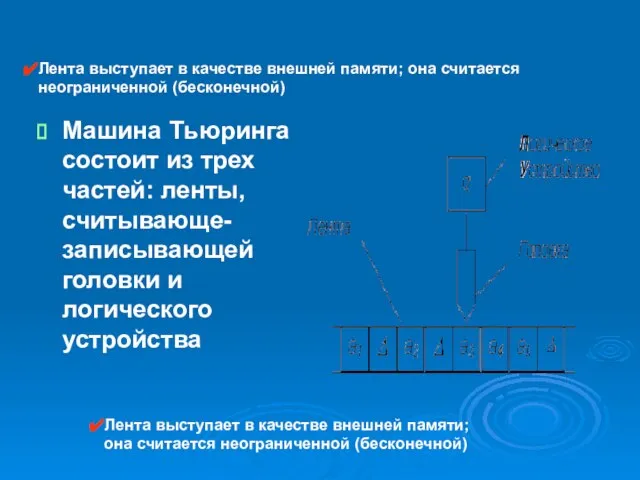
- 17. Лента выступает в качестве внешней памяти; она считается неограниченной (бесконечной) Машина Тьюринга состоит из трех частей:
- 18. Головка неподвижна, а лента передвигается относительно нее вправо или влево. Машина работает в некотором произвольном конечном
- 19. В каждую ячейку ленты может быть записан лишь один символ. Информация, хранящаяся на ленте, изображается конечной
- 20. Система исполняемых головкой команд предельно проста: на каждом такте она производит замену знака в обозреваемой ячейке
- 21. Команды перемещений ленты на ячейку влево, на ячейку вправо остаться на месте, т.е. адрес обозреваемой ячейки
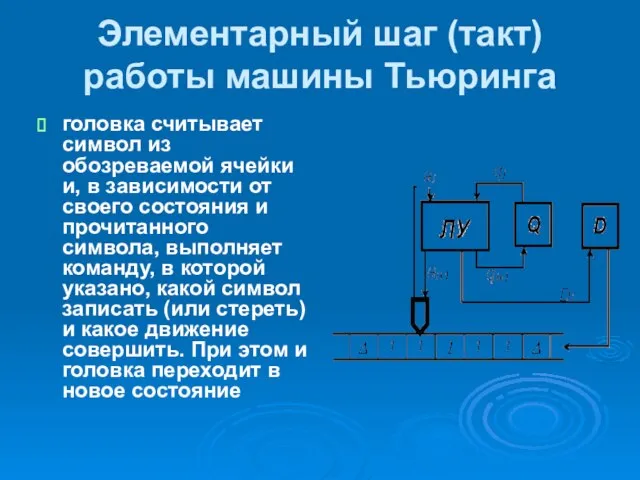
- 22. Элементарный шаг (такт) работы машины Тьюринга головка считывает символ из обозреваемой ячейки и, в зависимости от
- 23. Определение Конфигурация машины- совокупность состояний всех ячеек ленты, состояния ЛУ и положение головки В зависимости от
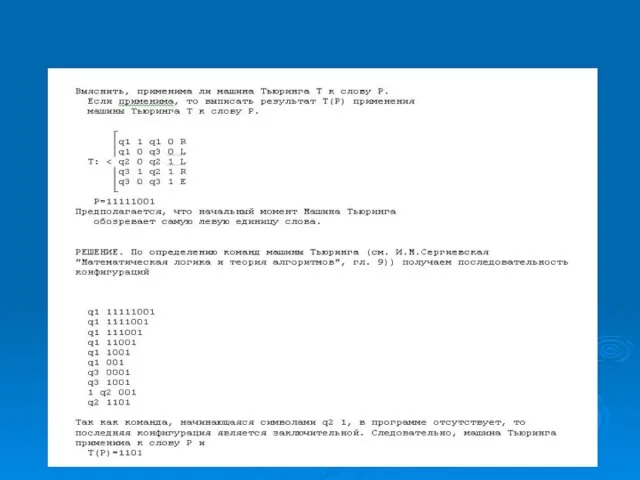
- 24. Пример Пусть начальной является конфигурация 1q11111. Такт 1 Обозревается 1, в ЛУ состояние q. Выходная команда
- 25. Тезис Тьюринга Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине
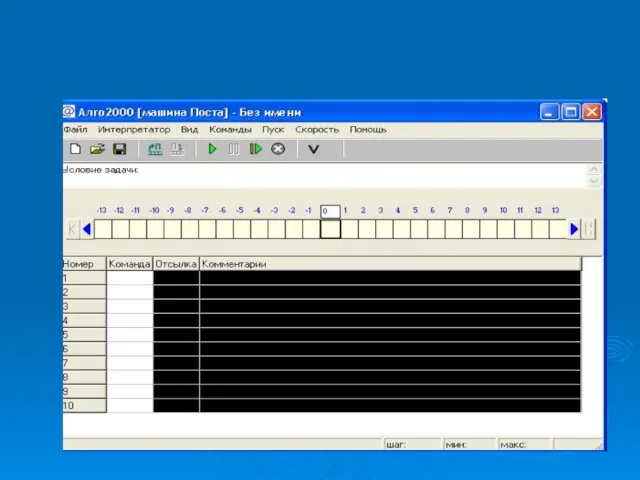
- 29. Алгоритмическая машина Поста Абстрактная машина Поста состоит из бесконечной ленты, разделенной на равные секции, считывающе-записывающей головки.
- 30. За один такт (его называют шагом) головка может сдвинуться на одну секцию вправо или влево и
- 31. Структура команды Каждая команда имеет следующую структуру xKy, x – номер исполняемой команды; K – указание
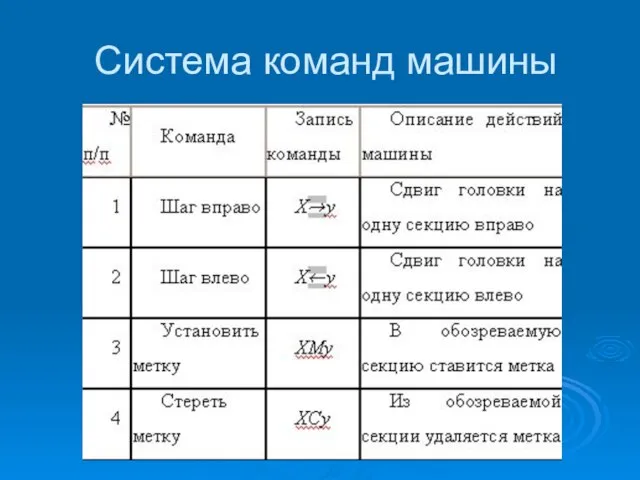
- 32. Система команд машины
- 33. Система команд машины
- 35. Комментарий к примеру Последовательное исполнение команд 1 и 2 приводит к тому, что головка за два
- 37. Скачать презентацию



























 Полиграфия
Полиграфия Омонимы. 2 класс
Омонимы. 2 класс Говорящий хомяк. Всегда поднимет настроение
Говорящий хомяк. Всегда поднимет настроение Презентация на тему Мясо птицы
Презентация на тему Мясо птицы  Технология изготовления изделий
Технология изготовления изделий Cодержание и основные задачи современного документационного обеспечения управления
Cодержание и основные задачи современного документационного обеспечения управления Криптовалюта first-coin
Криптовалюта first-coin Защита цифрового контента в кабельных сетях Примеры «Облачных» решений Conax в Восточной ЕвропеДни кабельного телевидения Украины
Защита цифрового контента в кабельных сетях Примеры «Облачных» решений Conax в Восточной ЕвропеДни кабельного телевидения Украины Энергетика, автоматика и системы коммуникаций
Энергетика, автоматика и системы коммуникаций Презентация на тему Микроорганизмы
Презентация на тему Микроорганизмы Гражданское право. 9 кл
Гражданское право. 9 кл Работа должна доставлять удовольствие!
Работа должна доставлять удовольствие! Видеоролики в instagram
Видеоролики в instagram «Состояние, актуальные проблемы и перспективы развития системы образования города Снежинска»
«Состояние, актуальные проблемы и перспективы развития системы образования города Снежинска» Центр детского развития Семицветик
Центр детского развития Семицветик Снеговик: история происхождения. Значение
Снеговик: история происхождения. Значение Процентные расчеты на каждый день
Процентные расчеты на каждый день Формирование положительного образа региона
Формирование положительного образа региона Кто придумал первую ракету?
Кто придумал первую ракету? Презентация на тему: Уроки литературы 11 класс ПЬЕСА М.ГОРЬКОГО «НА ДНЕ». ОСОБЕННОСТИ ЖАНРА И КОНФЛИКТА
Презентация на тему: Уроки литературы 11 класс ПЬЕСА М.ГОРЬКОГО «НА ДНЕ». ОСОБЕННОСТИ ЖАНРА И КОНФЛИКТА Merry christmas and happy new year
Merry christmas and happy new year Ведущие идеи построения региональной модели сопровождении одаренных детей
Ведущие идеи построения региональной модели сопровождении одаренных детей Варианты нормальной анатомии головного мозга на МР изображении
Варианты нормальной анатомии головного мозга на МР изображении Частые и популярные вопросы, а также помощь новичку.
Частые и популярные вопросы, а также помощь новичку. Развитие жизни в палеозойской эре
Развитие жизни в палеозойской эре Развитие жизни на Земле
Развитие жизни на Земле Ашан Скай мол
Ашан Скай мол Отчет по результатам диагностики адаптации учащихся 1 классов
Отчет по результатам диагностики адаптации учащихся 1 классов