Лекция 5Хранение информации в памяти компьютера (продолжение)

План урока:
Представление числовой информации в памяти ЭВМ
Представление текстовой информации в памяти ЭВМ
Представление графической информации в памяти ЭВМ

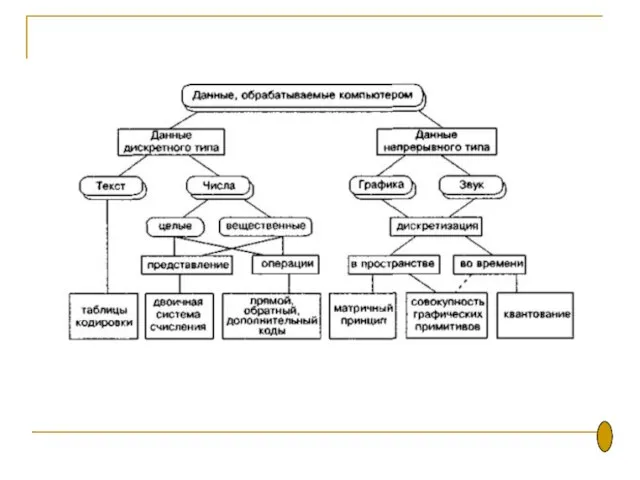
2. Представление текстовой информации в памяти ЭВМ

Таблицы кодировки
Таблица кодировки — таблица, содержащая упорядоченный перечень кодируемых символов, в соответствии с которой происходит преобразование символа в его двоичный код и обратно.
Наиболее популярные таблицы кодировки: ASCII (N=256) и Unicode (N=65535)
Минимальная длина кода (i) для кодирования любого знака из N- символьного алфавита определяется по формуле
2 i = N

ASCII-код 1960г
Стандартная часть
от 00 до 7F ,
- от 00 до 1F – управляющие коды, отданы производителям аппаратных средств
- от 20 (пробел) до 7F – английский алфавит, знаки препинания, цифры, арифметические операции
Расширенная часть
от 80 до FF
Символы национальных алфавитов, символы псевдографики, некоторые научные символы

Unicode (1993г)
Снимает ограничение однобайтовых таблиц – невозможность одновременного использования нескольких языков
В Unicode на кодирование символов отводится 32 бит (сколько символов может быть закодировано в этой таблице?)
0-127совпадают с ASCII,
далее алфавиты современных языков (до 65536)
В современных компьютерах и операционных системах используется укороченная, 16-битовая версия Unicode

Кодирование и декодирование с помощью таблицы ASCII
1. Зашифруйте текст «Принтер», используя таблицу ASCII-кодов.
2. Дешифруйте текст «42 69 6E 61 72 79», используя таблицу ASCII-кодов.
3. Используя объемный подход, посчитайте количество информации в сообщении: «Теоретические основы информатики».
(Символы закодированы с помощью таблицы ASCII)‏

3. Представление графической информации

Общие подходы к представлению в компьютере информации естественного происхождения
Для преобразования «естественной» информации в дискретную форму ее подвергают дискретизации и квантованию

Дискретизация
Дискретизацией (англ. discretisation) называют процедуру устранения временной и/или пространственной непрерывности естественных сигналов, являющихся носителями информации

Пространственная дискретизация
При пространственной дискретизации изображения его разбивают на небольшие области, в пределах которых характеристики изображения считают неизменными.

Временная дискретизация
При временной дискретизации время разбивают на небольшие интервалы, в пределах которых характеристики природных сигналов, как и в пространственном случае, считают неизменными
Пример. Временная дискретизация движущегося изображения
Пример. Временная дискретизация звукового сигнала

Квантование
Квантованием (англ. quantisation) называют процедуру преобразования непрерывного диапазона всех возможных входных значений измеряемой величины в дискретный набор выходных значений

Пример. Пример квантования цветовых оттенков серого цвета
1) Диапазон возможных значений измеряемой величины разбивается на несколько поддиапазонов.
2) При измерении определяется поддиапазон, в который попадает значение, и в компьютере сохраняется только номер поддиапазона.
Пусть яркость серого оттенка составляет 70%. Это значение попадает в поддиапазон 4(67% - 83%), поэтому в компьютере этот оттенок серого будет закодирован числом 4.

Графическое изображение – совокупность световых сигналов на плоскости
Можно измерять (выражать в числах) местоположение, цветовой оттенок и яркость каждого сигнала
Каждая характеристика может принимать любое из бесконечного множества значений в некотором диапазоне – все их невозможно представить в компьютере
Поэтому все измеряемые непрерывные характеристики подвергают дискретизации и квантованию

Дискретизация – выделение в неприрывном объекте конечного числа элементов, информация о которых будет сохранена в компьютере.
Информация об остальных элементах будет утеряна!
Квантование - формирование чисел, характеризующих эти элементы

Компьютерное изображение живописного произведения , цифровая запись музыкального произведения всегда отличаются от оригиналов в худшую сторону
Дискретизация и квантование всегда приводят к потере некоторой доли информации.
Выводы

Пространственная дискретизация изображений

Векторное и растровое представление графической информации
Растровое представление можно охарактеризовать как поточечное представление изображения
Векторное — как структурное представление изображения

Растровое представление
При растровой пространственной дискретизации графической информации на изображение накладывается сетка (растр), каждая ячейка которой (пиксель) рассматривается как далее неделимый фрагмент, определяемый набором атрибутов: координатами, формой, размером и цветом.
Процедура разбиения изображения на пиксели называется растеризацией, или оцифровкой, изображения.

Положение каждого пикселя на экране можно вычислить, зная только размеры растровой матрицы и линейные размеры пикселей либо плотность размещения пикселей, которую обычно измеряют в количестве точек на дюйм (dpi, Dots Per Inch).

Размер сетки растра , задаваемый в виде M*N,
где M - число пикселей по горизонтали, N – число пикселей по вертикали называется разрешающей способностью (или графическим разрешением) экрана.
Видеопамять – оперативная память, хранящая видеоинформацию во время ее воспроизведения в изображение на экране ( может делиться на страницы).
Страница – раздел видеопамяти, вмещающий информацию об одном образе экрана (одной картинке)
Графический файл – файл, хранящий информацию о графическом изображении.
Стандартные значения графического разрешения экрана :
640*480 800*600 1024*768 1280*1024 1600*1200

Векторное представление
Векторная пространственная дискретизация - это разбиение изображения на набор графических примитивов (кривая, прямая, окружность и др.)
Векторное представление изображения соответствует математическому описанию объектов с использованием системы координат
Построение векторного представления называется векторизацией изображения

Векторное представление
Изображение строится при помощи заранее определенного набора стандартных геометрических фигур

Квантование цвета графических изображений

Квантованию в случае растрового и векторного представления графической информации подвергается цвет точек изображения или графических примитивов

Математические модели цвета
Квантование (кодирование) цвета базируется на математическом описании цвета, которое, в свою очередь, опирается на тот факт, что цвета можно измерять и сравнивать
Научная дисциплина, изучающая вопро­сы измерения цветовых характеристик, называется метрологией цвета, или колориметрией

Объяснение процесса цветовосприятия
Теория Аристотеля (до сер. XVII века ) - все цвета образуются при подмешивании черного цвета к белому

Объяснение процесса цветовосприятия
Заложил основы современной теории цветов
Показал, что белый свет не первичен.
Выделил с помощью призмы в спектре белого света семь наиболее заметных спектральных цветов и назвал их основными (далее не разложимыми)— красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый.
Исаак Ньютон (1642 — 1727)

Объяснение процесса цветовосприятия
В 1756 г. сформулировал трехкомпонентную теорию восприятия цветов:
в глазу имеются три вида приемников лучистой энергии (колбочек), воспринимающих красную (длинноволновую), желтую (средневолновую) и голубую (коротковолновую) части видимого спектра.
Для получения любого цвета достаточно использовать всего три основные краски

Подобные гипотезы были выдвинуты
в Англии Томасом Юнгом в 1807 г.
в Германии Гемгольцем в 1852 г.
в этих гипотезах за основные цвета были приняты красный, зеленый и синий.
Наши ощущения — результат смешения (суммирования) в различных пропорциях этих цветов

Физиологическое обоснование трех компонентной модели цвета
Человеческий глаз содержит четыре типа зрительных рецепторов: «палочки» (рецепторы интенсивности) и три типа «колбочек» (рецепторы цветовых оттенков).
Колбочки каждого типа чувствительны к свету в своем узком диапазоне длин волн.
10 миллионов цветов

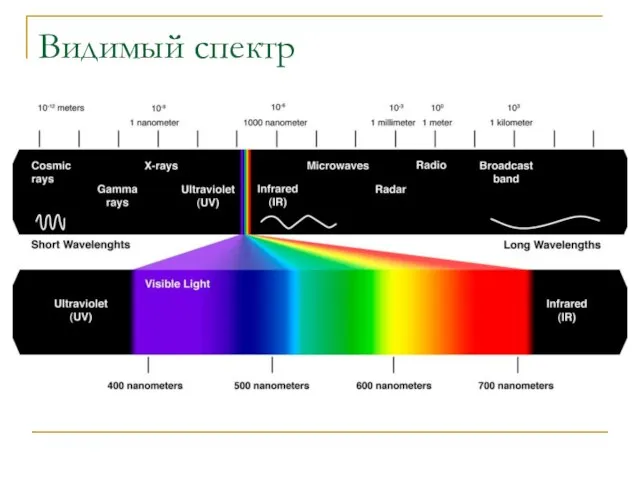
Видимый спектр

Математический аппарат для трехкомпонентной теории цвета (законы Грассмана)
Закон трехмерности : с помощью трех выбранных линейно независимых цветов можно однозначно выразить любой цвет.
(Цвета считаются линейно независимыми, если никакой из них нельзя получить путем смешения остальных)
Закон непрерывности : при непрерывном изменении излучения цвет смеси также меняется непрерывно.
(К любому цвету можно подобрать бесконечно близкий цвет)
Закон аддитивности : все цвета равноправны, разложение цветов можно выполнять по любым независимым цветам.

Законы Грассмана устанавливают общие свойства математических моделей цвета:
Любому цвету можно однозначным образом поставить в соответствие некоторую точку трехмерного пространства
Абсолютно черному цвету всегда соответствует точка (0, 0, 0)
Цвета можно рассматривать как точки или векторы в трехмерном цветовом пространстве

Цветовые модели
Каждая цветовая модель задает в трехмерном цветовом пространстве некоторую систему координат, в которой основные цвета модели играют роль базисных векторов.
RGB (Red-Green-Blue, красный-зеленый-синий).
CMYK (Cyan-Magenta-Yellow-blacK, голубой-пурпурный-желтый-черный) .
HSB (Hue-Saturation-Brightness, цветовой оттенок-насыщенность-яркость).

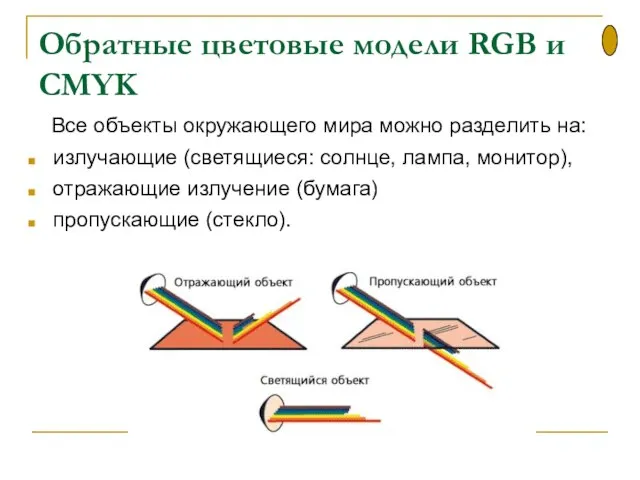
Обратные цветовые модели RGB и CMYK
Все объекты окружающего мира можно разделить на:
излучающие (светящиеся: солнце, лампа, монитор),
отражающие излучение (бумага)
пропускающие (стекло).

Цветовая модель RGB – описание цвета излучающего объекта
Модель RGB используется в телевизорах, мониторах, проекторах, сканерах, цифровых фотоаппаратах…
Основные цвета в этой модели: красный (Red), зеленый (Green), синий (Blue).

Формирование цвета в модели RGB
Модель RGB является аддитивной (суммарной), что означает, что цвета в этой модели добавляются к черному цвету.
Пиксель монитора излучает свет с помощью трех субэлементов: красного (Red), зеленого (Green), синиго (Blue).
Чтобы создать на экране основной цвет, надо включить (добавить к черному цвету) субэлемент определенного типа
Для получения составного цвета надо дополнительно включить (т. е. добавить) субэлементы другого типа

Цветовая модель RGB
R+G=Y;
G+B=C;
B+R=M.
Парное сочетание основных цветов в равных долях дает дополнительные цвета: желтый (Yellow), голубой (Cyan) и пурпурный (Magenta).
Сумма всех трех основных цветов в равных долях дает белый (White) цвет:
R+G+B=W.

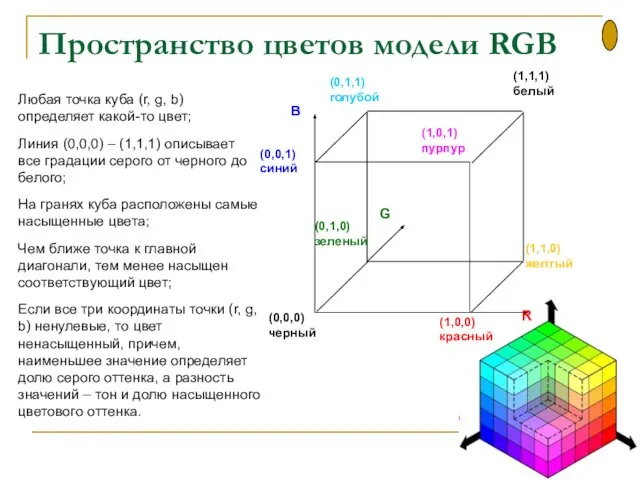
Пространство цветов модели RGB
Любая точка куба (r, g, b) определяет какой-то цвет;
Линия (0,0,0) – (1,1,1) описывает все градации серого от черного до белого;
На гранях куба расположены самые насыщенные цвета;
Чем ближе точка к главной диагонали, тем менее насыщен соответствующий цвет;
Если все три координаты точки (r, g, b) ненулевые, то цвет ненасыщенный, причем, наименьшее значение определяет долю серого оттенка, а разность значений – тон и долю насыщенного цветового оттенка.

Цветовая модель CMYK – описание цвета отражающего объекта
Цветовая модель CMYK используется в полиграфии при формировании изображений, предназначенных для печати на бумаге.
Основными цветами в ней являются: голубой (Cyan), пурпурный (Magenta), желтый (Yellow)

Формирование цвета в модели CMYK
Модель CMYK является субтрактивной (вычитательной), что означает, что цвета в этой модели получаются вычитанием цветов RGB из белого цвета.
Бумага отражает падающий свет, который обычно является «белым»
Краски на бумаге поглощают лучи определенного цвета, а остальные отражают.
Видимый нами цвет краски определяется теми лучами, которые не были поглощены.
Таким образом, краски вычитают, или ослаблятют цвета в отражаемом потоке света.

CMYK
C=W-R;
M=W-G;
Y=W-B
Парное сочетание в равных долях цветов модели CMY дает цвета модели RGB
В теории, сумма C+M+Y=K, т.е. дает черный (blacK) цвет,
на практике это затруднительно, поэтому в модели CMYK к триаде CMY добавляют черный цвет K

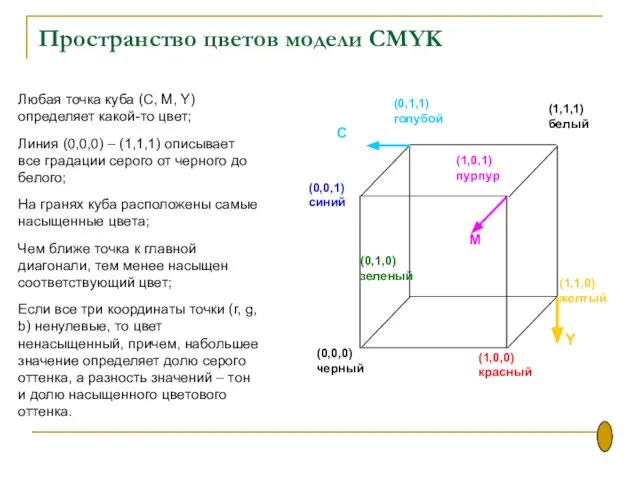
Пространство цветов модели CMYK
Любая точка куба (С, M, Y) определяет какой-то цвет;
Линия (0,0,0) – (1,1,1) описывает все градации серого от черного до белого;
На гранях куба расположены самые насыщенные цвета;
Чем ближе точка к главной диагонали, тем менее насыщен соответствующий цвет;
Если все три координаты точки (r, g, b) ненулевые, то цвет ненасыщенный, причем, набольшее значение определяет долю серого оттенка, а разность значений – тон и долю насыщенного цветового оттенка.

Цветовая модель HSB
Основой для модели HSB (Hue, Saturation, Brightness), она же HSL (Hue, Saturation, Lightness) - являются 3 параметра:
Тон (Hue),
Насыщенность (Saturation),
Яркость (Brightness)

Цветовая модель HSB
(Hue-Saturation-Brightness)
(цветовой тон-насыщенность-яркость)
Чистый цветовой тон – один из цветов спектрального разложения цвета.
Цветовой оттенок – смесь чистого цветового тона с серым цветом.
Насыщенность цвета – доля чистого тона в цветовой смеси.
Яркость характеризуется общей светлостью смешиваемых цветов

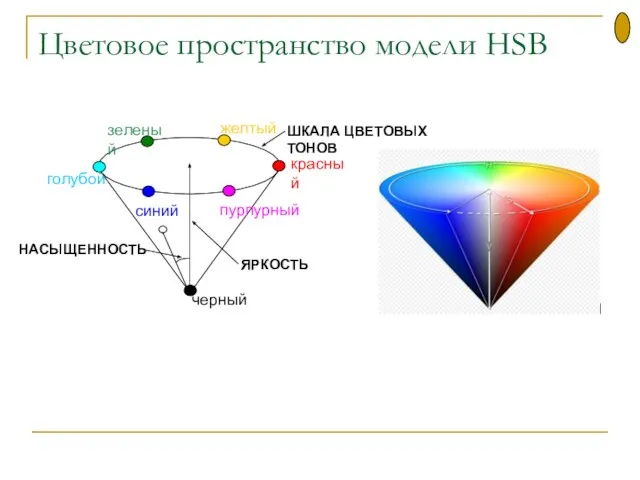
Цветовое пространство модели HSB

Cпособы «разворачивания» трёхмерного пространства HSB на двухмерный экран компьютера
Цветовой круг - эта визуализация состоит из цветового круга (то есть, поперечного сечения цилиндра) и движка яркости (высоты цилиндра).

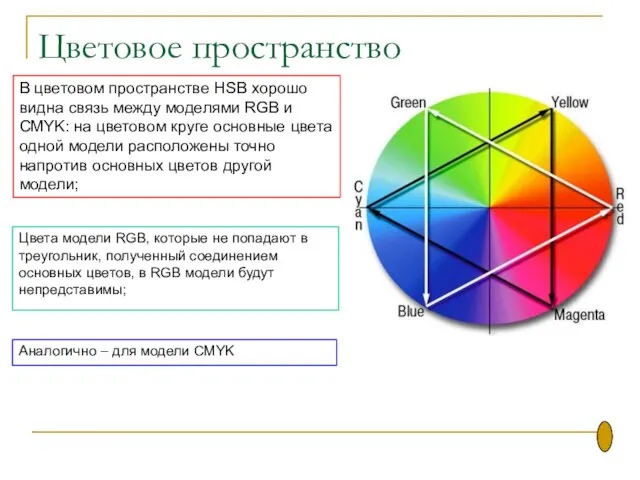
Цветовое пространство
В цветовом пространстве HSB хорошо видна связь между моделями RGB и CMYK: на цветовом круге основные цвета одной модели расположены точно напротив основных цветов другой модели;
Цвета модели RGB, которые не попадают в треугольник, полученный соединением основных цветов, в RGB модели будут непредставимы;
Аналогично – для модели CMYK

ВЫВОДЫ: Модель HSB позволяет закодировать практически все цвета, воспринимаемые человеком.
Модели RGB и CMYK описывают возможности компьютерных устройств по воспроизведению цвета.
Некоторые цвета в принципе не могут быть воспроизведены на компьютере

Квантование (кодирование) цветового пространства

Квантование цветового пространства
Квантование достигается переводом вещественных чисел из интервала [0; 1) в интервал целых чисел от 0 до N - 1 путем умножения на целое число N, с последующим округлением.
Интервал [0; 1) каждой цветовой оси разбивается на N равных подинтервалов
После квантования каждый цвет представляется триадой целых неотрицательных чисел
(kr, kg ,kb), 0 ≤ ki < N
N – количество цветов

Глубина цвета
Число N выбирают степенью 2
N = 2i
Величину i называют глубиной цвета
i – количество бит, которым кодируется 1 пиксель (сумма бит, которыми кодируются каждая компонента цвета)
i = ir+ig+ib

Глубина цвета
Количество бит, используемых для кодирования цвета одной точки называется глубиной цвета (битовой глубиной, цветовым разрешением)
От глубины цвета зависит количество отображаемых цветов, которое может быть вычислено по формуле:
N=2k,
где N – количество отображаемых цветов,
k – глубина цвета.
Наиболее распространенными значениями глубины цвета являются 4, 8, 16 или 24 бита на точку.

Пример: для кодирования одной компоненты цвета используется 1 бит
i = 1+1+1 = 3 бит N = 23 = 8 цветов

Пример: для кодирования компонент R и B используется 5 бит, компоненты G – 6 бит (стандарт HighColor )
i = 5+5+6 = 16 бит N = 216 = 65536 цветов

Пример: для кодирования одной компоненты цвета используется 1 байт (стандарт TrueColor )
i = 8+8+8 = 24 бит N = 224 = 16777216 цветов

Квантование цветового пространства в модели HSB
В ОС Windows каждая из HSB-xaрактеристик описывается одним байтом

Битовая карта изображения
Битовая карта является двоичным кодом изображения, хранится в видеопамяти компьютера, считывается видеопроцессором ( не реже 60 раз в секунду – частота обновления экрана) и отображается на экран.
Битовая карта черно-белого изображения будет выглядеть так:
00000000
00100100
00101000
00110000
00110000
00101000
00100100
00100010
Битовая карта при трехбитном кодировании изображения будет выглядеть так:
011 011 011 011 011 011 011 011
011 011 001 011 011 001 011 011
011 011 001 011 001 011 011 011
011 011 001 001 011 011 011 011
011 011 001 001 011 011 011 011
011 011 001 011 001 011 011 011
011 011 001 011 011 001 011 011
011 011 001 011 011 011 001 011
Информационный объем изображения
I=8*8*1(бит)=64 бита=8 байт
Информационный объем изображения
I=8*8*3(бит)=192 бита=24 байт

При масштабировании (изменении размеров изображения) качество растрового изображения значительно ухудшается
При увеличении проявляется «пикселизованность» - контуры становятся ступенчатыми (добавляются лишние точки с цветом соседней точки)
При уменьшении безвозвратно теряется часть информации (уменьшается количество точек)
Несжатое полноцветное растровое изображение занимает значительное место в памяти компьютера.

Векторная графика
В векторном представлении графическое изображение на экране формируется из объектов – линий, прямоугольников, окружностей, дуг, закрасок – которые называются графическими примитивами.
В этом случае графическая информация – это данные, однозначно определяющие все графические примитивы, составляющие рисунок (координаты, толщину линий, цвет).
Векторные команды:
Цвет черный
Линия 3, 2, 3, 8
Линия 4, 4, 6, 2
Линия 4, 5, 7, 8
Векторное изображение занимает значительно меньше места, легко масштабируется, при этом качество изображения не ухудшается.

Ответьте письменно на вопросы
1) Изображение разбивают на графические примитивы. Что это за процедура: дискретизация или квантование? Какое изображение будет сформировано после этой процедуры растровое или векторное?
2) Сколько базовых цветов нужно использовать, чтобы воспроизвести любой из видимых цветов?
3) Какую цветовую модель нужно выбрать в графическом редакторе, если вы создаете изображение, которое будет демонстрироваться только с экрана компьютера?
4) Какая цветовая модель позволяет закодировать все видимые цвета спектра, в том числе те, которые не представимы на компьютере?
5) Сколько цветов можно использовать в изображении, если для кодирования одного цвета в памяти компьютера используется 16 бит?

Форматы графических файлов.
Windows Bit MaP (расширение файлов - .bmp) – формат операционной системы Windows для хранения растровых изображений; поддерживается всеми Windows-приложениями.
TIFF (Tagged Image File Format) (расширение файлов - .tif) – предназначен для хранения растровых изображений высокого качества в широком цветовом диапазоне; поддерживается большинством графических, издательских и дизайнерских программ;
GIF (Graphic Interchange Format) (расширение файлов - .gif) – стандартизирован в 1987 г. как средство хранения изображений с фиксированным (256) количеством цветов. Из-за ограниченных цветовых возможностей применяется исключительно в электронных публикациях. Благодаря компактности файлов широко используется для размещения графических изображений на Web-страницах в Интернете
JPEG (Joint Photographic Experts Group) (расширение файлов - .jpg) –обеспечивает хранение растровых графических изображений в более компактной форме на основе использования эффективного алгоритма сжатия. Применяемые методы сжатия основаны на удалении «избыточной» информации. Позволяет регулировать соотношение между степенью сжатия файла и качеством изображения.
PSD (PhotoShop Document) (расширение файлов - .psd) – собственный формат графического редактора Adobe Photoshop, один из наиболее мощных по возможностям хранения растровой графической информации.
PDF (Portable Document Format) (расширение файлов - .pdf) – разработан фирмой Adobe для хранения изображений документов (например, страниц книг, журналов и др.); является аппаратно-независимым (вывод изображений допустим на любых устройствах). Мощный алгоритм сжатия со средствами управления итоговым разрешением изображения обеспечивает компактность файлов при высоком качестве иллюстраций.
WMF (Windows MetaFile) (расширение файлов - .wmf) – формат операционной системы Windows для хранения векторных изображений; поддерживается всеми Windows-приложениями. Однако отсутствие средств для работы со стандартизированными цветовыми палитрами, принятыми в полиграфии, и другие недостатки ограничивают его применение.

Задание
Заполните таблицу, вычислив информационный объем графической информации при различных соотношениях графического и цветового разрешения.

Задача 1.
Закодируйте монохромный рисунок с помощью двоичного алфавита в соответствии с матричным принципом.
Решение.
Имеем матрицу 6Х9, всего 54 бита. Закрашенной клетке поставим в соответствие 1, незакрашенной – 0.
Получим: 011111 100010 100010 100010 011110 001010 010010 010010 110111
Сравните:
код буквы «я» в КОI8 - 11110001
ВЫВОД: Отсканированная страница текста занимает места в памяти больше, чем та же страница после распознавания текста (перевода рисунка в текстовый формат)

Задача 2.
Сколько места в памяти будет занимать тот же рисунок, если сохранить его в формате как
А) 256-цветный рисунок;
В) в режиме HighColor;
С) в режиме True Color?
Решение.
Рисунок разбит на 6*9=54 пикселя.
А) 256=28, т.е. код каждого пикселя передается 8 битами. I=54*1=54 байта
В) HighColor: 1 пиксель передается 16 битами (2 байта). I=54*2=108 байтов
С) TrueColor: цвет пикселя передается 24 битами (3 байта). I=54*3=162 байта (т.е. в 24 раза больше, чем монохромный)
ВЫВОД: Монохромный рисунок нужно сохранять именно как монохромный

Задача 3.
Какой объем видеопамяти необходим для хранения четырех страниц изображения, при условии, что разрешающая способность дисплея равна 640Х480 точек, а используемых цветов 32?
Решение.
1) N=2i, 32=2i, i=5 бит – глубина цвета
2) I=640*480*5*4=6144000 бит = 750 Кбайт
Ответ: 750 Кбайт

Задача 4.
265-цветный рисунок содержит 1 Кбайт информации. Из скольких точек он состоит?
Решение.
1) N=2i, 256=2i, i=8 бит – информационный объем одной точки;
2) 1 Кбайт =1024*8 бит =8192 бит - объем изображения;
3) 8192:8=1024 точек – на изображении
Ответ: 1024 точки

Задача 5.
На экране монитора необходимо получить 1024 оттенка серого цвета. Какой должна быть глубина цвета?
Решение.
1) 1024≅10*10*10 – по 10 бит приходится на каждую из трех составляющих (красную, зеленую, синюю) ;
2) 10*3 =30 бит - глубина цвета;
Ответ: 30 бит

Задача 6.
После преобразования графического изображения количество цветов уменьшилось с 256 до 32. Во сколько раз уменьшился объем занимаемой памяти?
Ответ: 1,6 раза
Решение.
1) N1=2i, 256=2i, i1=8 бит – информационный объем одной точки 1-го изображения;
2) N2=2i, 32=2i, i2=5 бит - информационный объем одной точки 2-го изображения;
3) i1/i2=8/5=1,6 раза

Задача 7.
Видеопамять имеет объем, в котором может храниться 8-цветное изображение размером 640Х350 точек. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 512-цветную палитру?
Ответ: 74667 точек
Решение.
N1=2i, 8=2i, i1=3 бита – глубина цвета 1-го изображения;
640*350*3=672000 бит – объем видеопамяти
3) N2=2i, 512=2i, i2=9 бит - информационный объем одной точки 2-го изображения;
3) 672000/9=74667 точек – размер 2-го изображения

Задание 1
Для хранения растрового изображения размером 128*128 пикселей отвели 4 кбайта памяти. Каково максимально возможное число цветов в палитре изображения.

Задание 2
Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать цветное растровое изображение размером 640*480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами

Задание 3
Укажите минимальный объем памяти (в килобайтах), достаточный для хранения любо растрового изображения размером 64*64 пикселя, если известно, что в изображении используется палитра из 256 цветов. Саму палитру хранить не нужно

Задание 4
Рассчитайте объем видеопамяти, необходимой для хранения графического изображения, занимающего весь экран монитора с разрешением 640 х 480 и количеством отображаемых цветов, равным 65 536.

Задание 5
Подсчитайте объем информации, передаваемой от видео­адаптера к монитору в видеорежиме 1024 х 768 пикселей с глубиной цвета 24 бита и частотой обновления экрана 85 Гц.