Лекция 10

Лекция № 10
Гистограммы. Построение и анализ.

Гистограммы
Статистический анализ случайных погрешностей подразумевает проведение многократных измерений. Если число измерений превышает 15-20, то их представление в виде таблицы или списка не удобно и не наглядно. В таких случаях результаты наглядно представить в виде гистограммы.
Допустим, получен ряд результатов измерений количества α - частиц, попавших в счетчик Гейгера за 1 мин. (26; 24; 26; 28; 23; 24; 25; 24; 26; 25). Если в серии измерений один и тот же результат встречается несколько раз, то можно подсчитать число реализаций каждого результата.

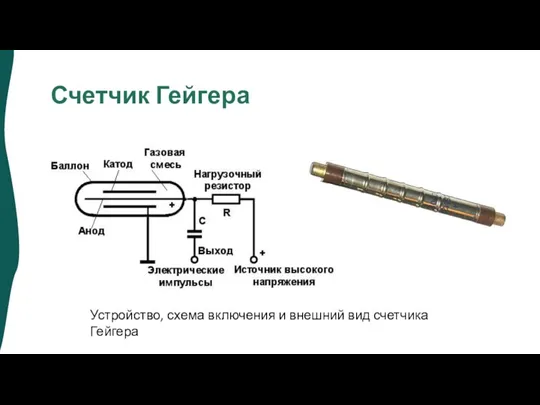
Счетчик Гейгера
Устройство, схема включения и внешний вид счетчика Гейгера

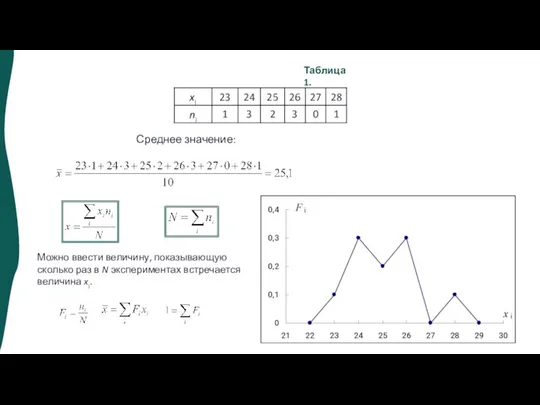
Таблица 1.
Среднее значение:
Можно ввести величину, показывающую сколько раз в N экспериментах встречается величина xi.
.

В большинстве случаев в физике приходится иметь дело с непрерывными физическими величинами.
Пример: пусть при помощи штангенциркуля произведены измерения длины и получены следующие результаты (в мм): (26,4; 23,9; 25,1; 24,6; 22,7; 23,8; 25,1; 23,9; 25,3; 25,4). Результаты практически не повторяются, поэтому для построения гистограммы необходимо разбить диапазон результатов измерений на равные интервалы-промежутки и подсчитать число попаданий в каждый интервал. Каждый такой интервал называется бином (карманом).

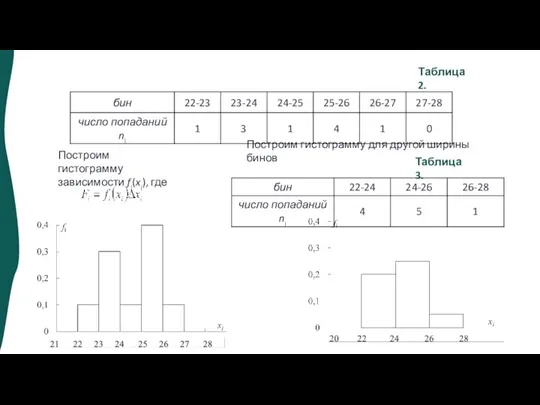
Таблица 3.
Построим гистограмму для другой ширины бинов
Таблица 2.
Построим гистограмму зависимости fi(xi), где

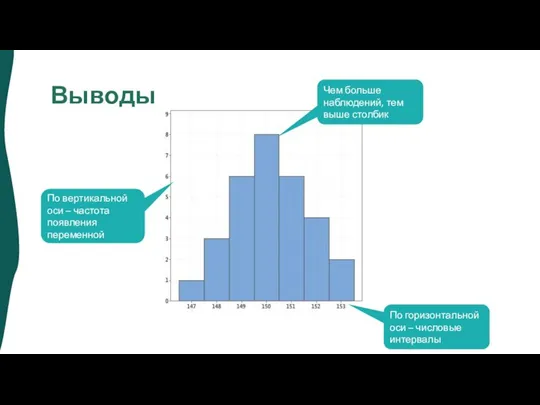
Выводы
По вертикальной оси – частота появления переменной
По горизонтальной оси – числовые интервалы
Чем больше наблюдений, тем выше столбик

Порядок построения гистограммы:
Собрать данные, выявить максимальное и минимальное значения и определить диапазон (размах) гистограммы.
Полученный диапазон разделить на интервалы, предварительно определив их число (обычно 5-20 в зависимости от числа показателей) и определить ширину интервала.
Все данные распределить по интервалам в порядке возрастания: левая граница первого интервала должна быть меньше наименьшего из имеющихся значений.
Подсчитать частоту попаданий результатов в каждый интервал.
Вычислить относительную частоту попадания данных в каждый из интервалов.
По полученным данным построить гистограмму - столбчатую диаграмму, высота столбиков которой соответствует частоте или относительной частоте попадания данных в каждый из интервалов:
- наносится горизонтальная ось, выбирается масштаб и откладываются соответствующие интервалы;
- затем строится вертикальная ось, на которой также выбирается масштаб в соответствии с максимальным значением частот.

Правило Стёрджеса - эмпирическое правило определения оптимального количества интервалов, на которые разбивается наблюдаемый диапазон изменения случайной величины при построении гистограммы плотности её распределения.
К выбору рекомендуемого числа интервалов на гистограмме:

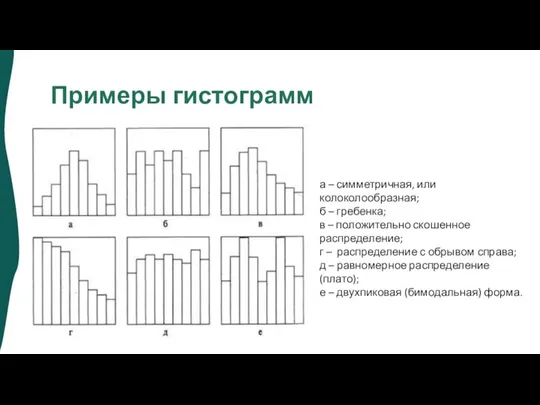
Примеры гистограмм
а – симметричная, или колоколообразная;
б – гребенка;
в – положительно скошенное распределение;
г – распределение с обрывом справа;
д – равномерное распределение (плато);
е – двухпиковая (бимодальная) форма.

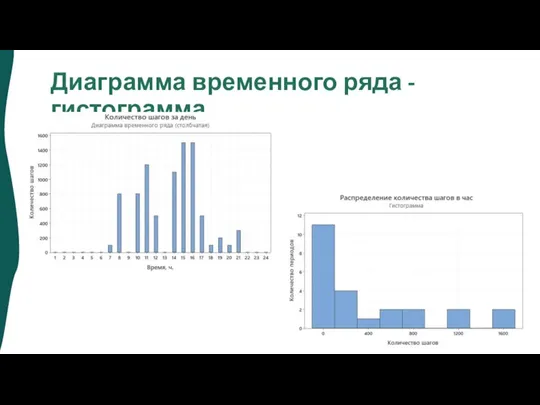
Диаграмма временного ряда - гистограмма

Как проводить анализ гистограмм?
Гистограммы нужны для того, чтобы наглядно представить распределение наблюдений. Но что еще мы можем увидеть, рассматривая прямоугольники, составляющие этот график? Какую информацию можем «прочесть»? На что обратить внимание и как это лучше сделать?
Визуальная оценка гистограмм позволяет воспринять ряд статистических показателей:
распределение наблюдений (distribution);
наибольшую концентрацию данных – моду (mode);
минимальное и максимальное значения (min и max);
размах (range);
степень асимметрии – скос (skewness);
эксцесс (kurtosis);
наличие явных выбросов (outliers);
возможное присутствие нескольких распределений (популяций);
ширину интервалов – дистанцию между правым и левым краями частотной ячейки по оси X;
количество интервалов – общее (в том числе и нулевые значения) количество частотных ячеек гистограммы.

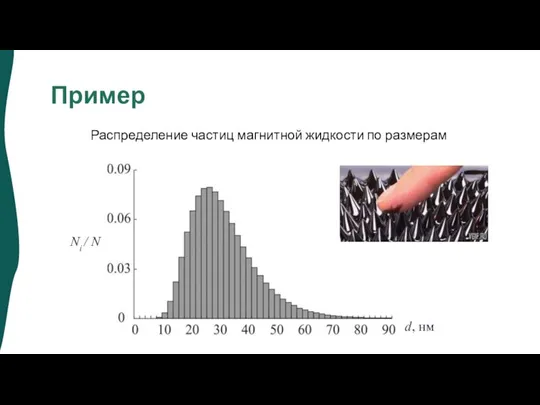
Пример
Распределение частиц магнитной жидкости по размерам