Содержание
- 2. Темы для СРС Типы поляризации диэлектриков
- 3. 1.1 Проводники и диэлектрики Все тела в природе можно условно разделить по их электрическим свойствам на
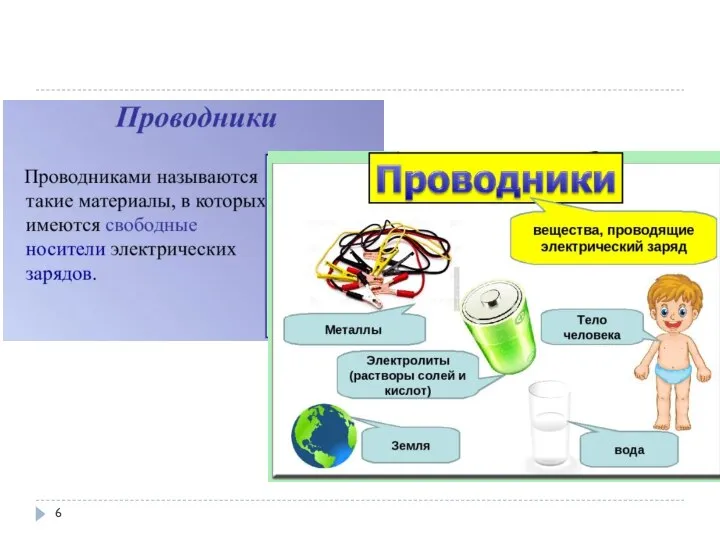
- 4. 1.1 Проводники
- 5. 1.1 Проводники
- 7. Понятие «диэлектрик» чаще всего употребляется в физике для обозначение материала, который не поводит электрический ток Изолятор
- 9. Для изготовления электронных приборов используют твердые полупроводники, имеющие кристаллическое строение. Полупроводниковые приборы - приборы, действие которых
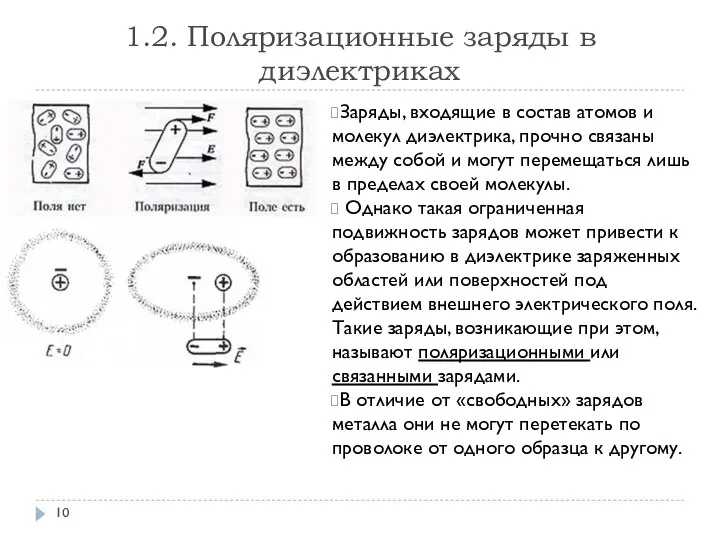
- 10. 1.2. Поляризационные заряды в диэлектриках Заряды, входящие в состав атомов и молекул диэлектрика, прочно связаны между
- 11. 1.3 Дипольная модель диэлектрика Процессы, происходящие в диэлектриках во внешнем поле, легко рассмотреть, если представить диэлектрик
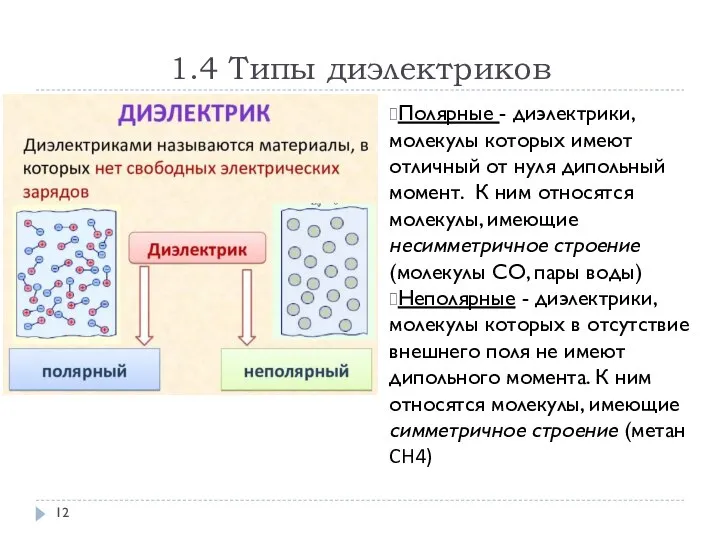
- 12. 1.4 Типы диэлектриков Полярные - диэлектрики, молекулы которых имеют отличный от нуля дипольный момент. К ним
- 13. 1.5 Вектор поляризации
- 14. 1.6 Поляризация диэлектриков В отсутствие внешнего поля вектор поляризации неполярного диэлектрика равен нулю. Во внешнем поле
- 15. 1.6 Поляризация диэлектриков Силы образуют пару, механический момент которой равен В результате молекулы приобретают частичную ориентацию
- 17. 1.7 Вектор поляризации и связанные заряды Плотность поляризованных зарядов определяется вектором поляризации Рассмотрим для простоты объем
- 18. 1.7 Вектор поляризации и связанные заряды В большинстве диэлектриков поляризация неоднородна, поэтому в них появляются объемные
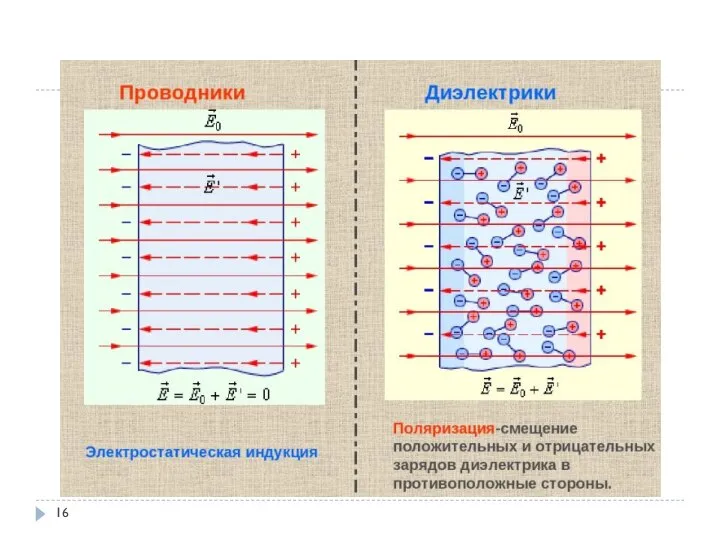
- 19. 1.8 Электрическое поле в диэлектриках Случай поля между двумя плоскопараллельными пластинами, между которыми находится диэлектрик. Результирующее
- 20. 1.9 Теорема Гаусса для диэлектриков. Электрическое смещение Влияние диэлектрика на электрическое поле сводится к действию поляризационных
- 21. 1.10 Сегнетоэлектрики Существует группа кристаллических диэлектриков – «сегнетоэлектрики», поляризуемость которых очень велика (χ ~ 104). Сегнетоэлектрики
- 22. 2.1 Электроемкость проводников. Электрическое поле заряженного проводника Если к проводнику добавить или отнять у него часть
- 23. 2.2 Электроемкость Увеличение заряда на проводнике пропорционально увеличению напряженности поля, что приводит в свою очередь к
- 24. 2.3 Емкость проводящей сферы Поле заряженной сферы обладает центральной симметрией, т.е. направление Е совпадает с направлением
- 25. 2.4 Конденсаторы На практике бывает необходимо иметь большие емкости, способные при небольшом потенциале накапливать значительный заряд.
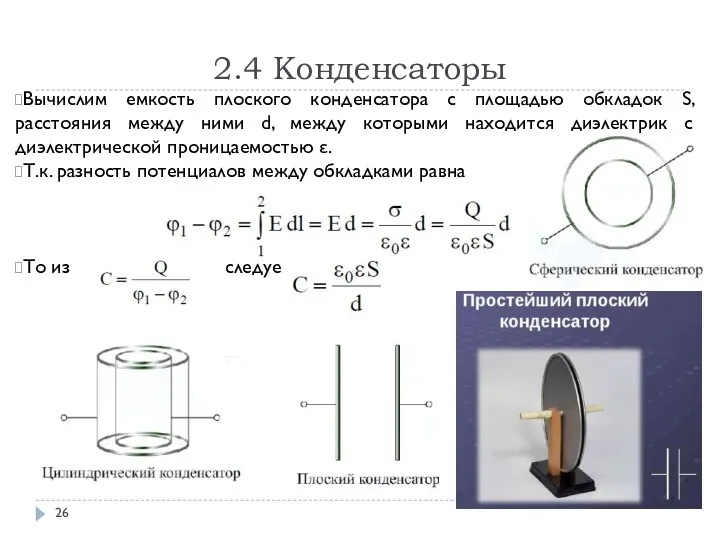
- 26. 2.4 Конденсаторы Вычислим емкость плоского конденсатора с площадью обкладок S, расстояния между ними d, между которыми
- 27. 2.4 Конденсаторы
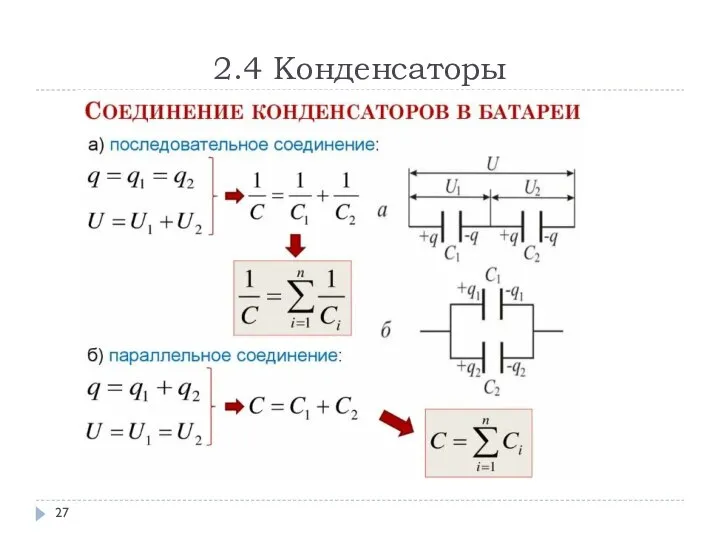
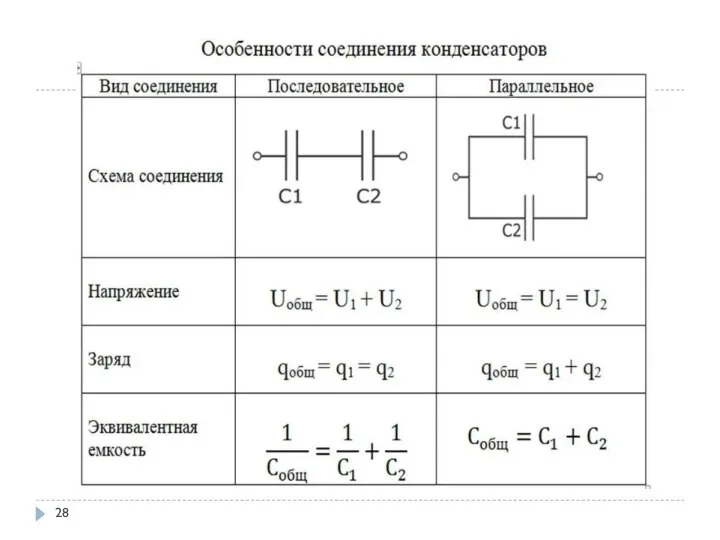
- 28. 2.4 Конденсаторы
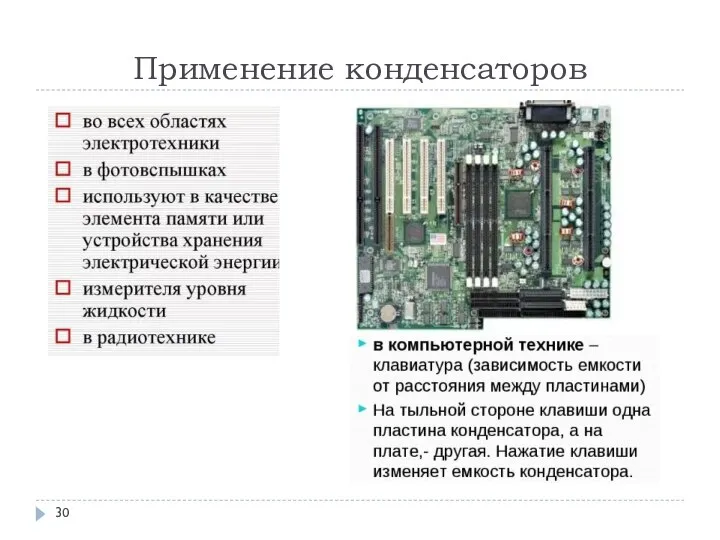
- 30. Применение конденсаторов
- 31. 2.5 Энергия электростатического поля Если соединить пластины заряженного конденсатора проводником, то начнется перемещение электрических зарядов, и
- 33. Скачать презентацию






















 Особенности истории России. Место России в мировом историческом процессе
Особенности истории России. Место России в мировом историческом процессе Оппортунистические инфекции
Оппортунистические инфекции  Всемирный день борьбы со СПИДом
Всемирный день борьбы со СПИДом Доказательная медицина и стандарты медицинской деятельности
Доказательная медицина и стандарты медицинской деятельности Система счетов и двойная запись
Система счетов и двойная запись Презентация на тему Лепка из пластилина
Презентация на тему Лепка из пластилина  Ночевала тучка золотая
Ночевала тучка золотая Revision
Revision Материально-производственная деятельность человека.
Материально-производственная деятельность человека. Как помочь ребёнку быть внимательным.
Как помочь ребёнку быть внимательным. Защитники земли русской. Работы учеников
Защитники земли русской. Работы учеников Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы
Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы  Словообразование (6 класс)
Словообразование (6 класс) 1 сентября. Классный час «От пера до компьютера».
1 сентября. Классный час «От пера до компьютера». Грамматические особенности перевода арабских фильмов на русский язык
Грамматические особенности перевода арабских фильмов на русский язык 1.3.2 Логические элементы ЭВМ
1.3.2 Логические элементы ЭВМ HTML
HTML Психологический климат в трудовом коллективе
Психологический климат в трудовом коллективе НОУ СОШ Гармония
НОУ СОШ Гармония Китайско-конфуцианская цивилизация
Китайско-конфуцианская цивилизация Каракули. Упражнение 2
Каракули. Упражнение 2 Презентация на тему Треугольники 7 класс геометрия
Презентация на тему Треугольники 7 класс геометрия  Moral Crisis in south Africa
Moral Crisis in south Africa Промоагентство
Промоагентство Презентация на тему Проблема темперамента и характера
Презентация на тему Проблема темперамента и характера Мой творческий путь в прозе и стихах
Мой творческий путь в прозе и стихах ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd.
ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd. Политические режимы. Типы политических режимов
Политические режимы. Типы политических режимов