Слайд 3 Перспективой называют центральную проекцию объекта, на которую наложены ограничения, связанные с особеннос-тями
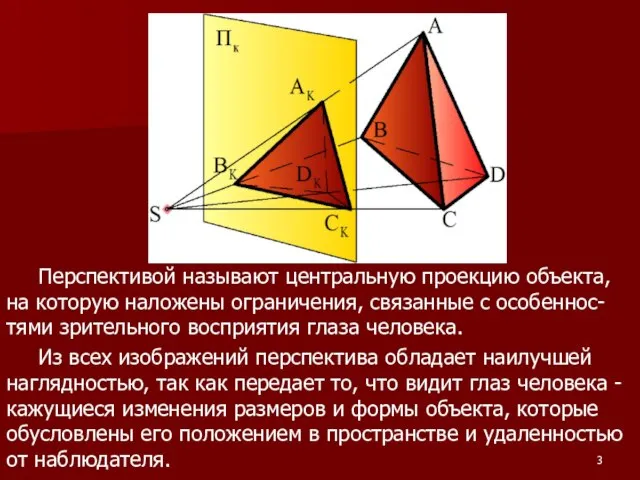
зрительного восприятия глаза человека.
Из всех изображений перспектива обладает наилучшей наглядностью, так как передает то, что видит глаз человека - кажущиеся изменения размеров и формы объекта, которые обусловлены его положением в пространстве и удаленностью от наблюдателя.
Слайд 6На плоскости – линейная перспектива.

Слайд 7Если плоскость расположена горизонтально, то перспектива плафонная (для росписи потолков).
На цилиндрической поверхности

– панорамная перспектива.
На сферической поверхности – купольная перспектива.
Слайд 8Система плоскостей линейной перспективы
Пк ⊥ П1
H II П1
Пк ∩ Н = h
Пк
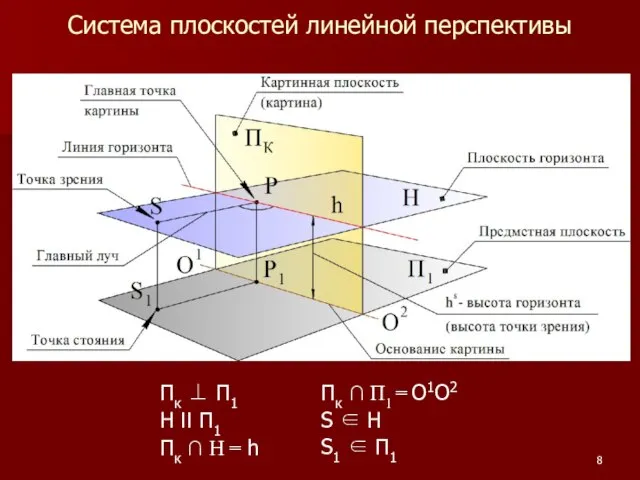
∩ П1 = О1О2
S ∈ H
S1 ∈ П1
Слайд 10Общий принцип построения перспективы точки
SA ∩ Пк = Ак Ак – перспектива
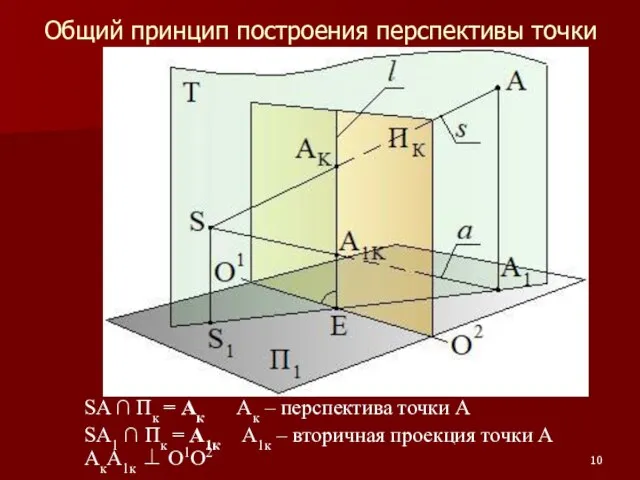
точки А
SA1 ∩ Пк = А1к А1к – вторичная проекция точки А АкА1к ⊥ О1О2
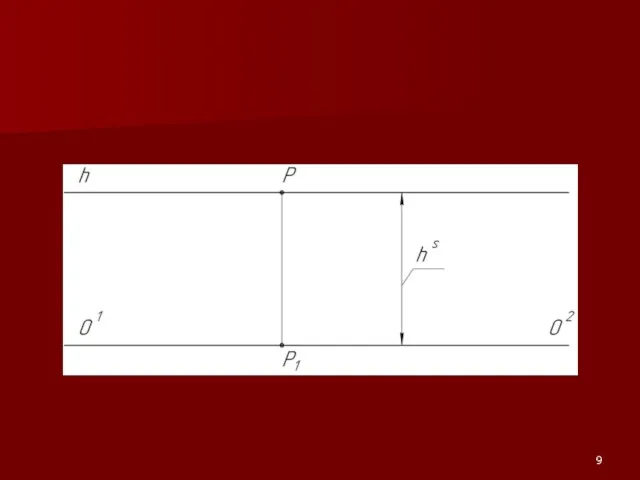
Слайд 11Перспектива точек предметного пространства
Если точка принадлежит картине, то ее вторичная проекция лежит
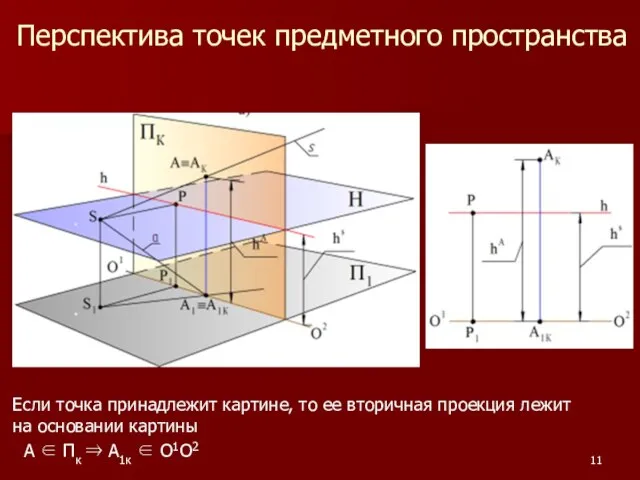
на основании картины
А ∈ Пк ⇒ А1к ∈ О1О2
Слайд 12Вторичная проекция несобственной точки пространства лежит на линии горизонта
F ≡ F∞
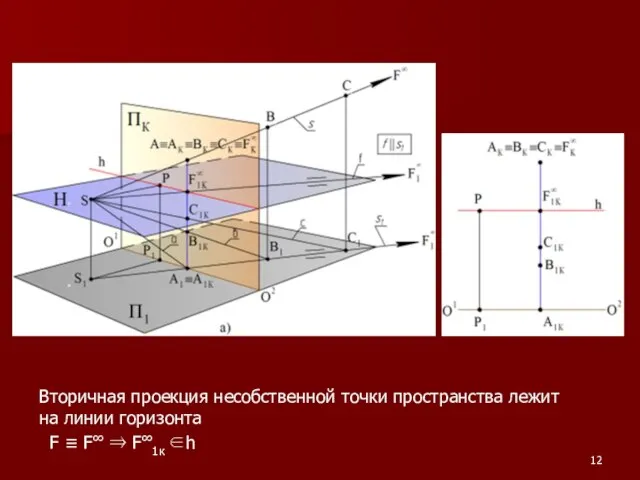
⇒ F∞1к ∈h
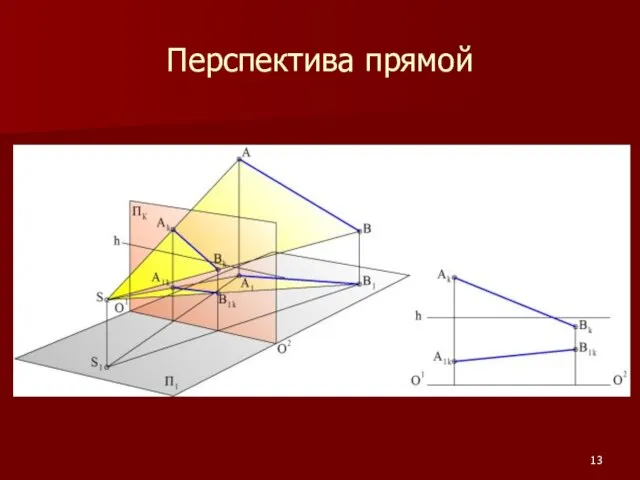
Слайд 14В перспективе прямая задается двумя точками
m (N, F∞)
Точка N – начало прямой.

Принимается точка пересечения прямой с картинной плоскостью.
N = m ∩ Пк
Точка F∞ - несобственная точка.
N∈Пк ⇒ Nк ≡ N ∧ N1к∈O1O2; F∞ ⇒ F1к∈ h.
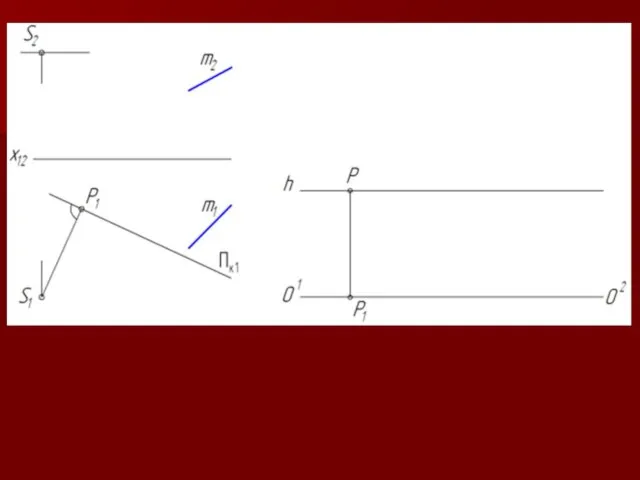
Слайд 16Чтобы получить точку N начала прямой m, необходимо продолжить прямую до пересечения

с картинной плоскостью
m ∩ Пк= N
Чтобы получить (увидеть) несобственную точку F∞, принадлежащую прямой m, находясь в точке зрения S, необходимо направить луч зрения параллельно прямой m.
Точка F∞k пересечения луча s с картинной плоскостью Пk и будет изображением несобственной точки F∞.
S∈s, s II m и s ∩ Пk = F∞k
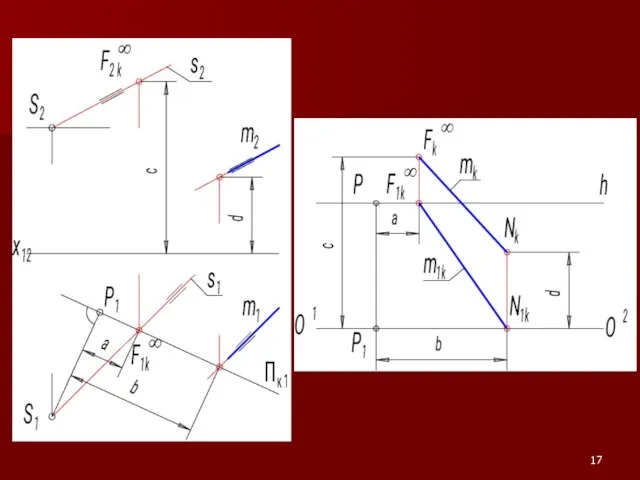
Слайд 18∞
По положению точки F∞k относительно линии горизонта
можно судить о положении прямой

m относительно
предметной плоскости.
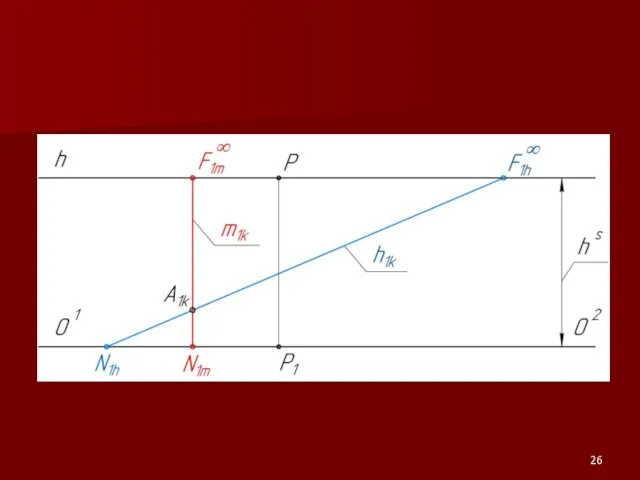
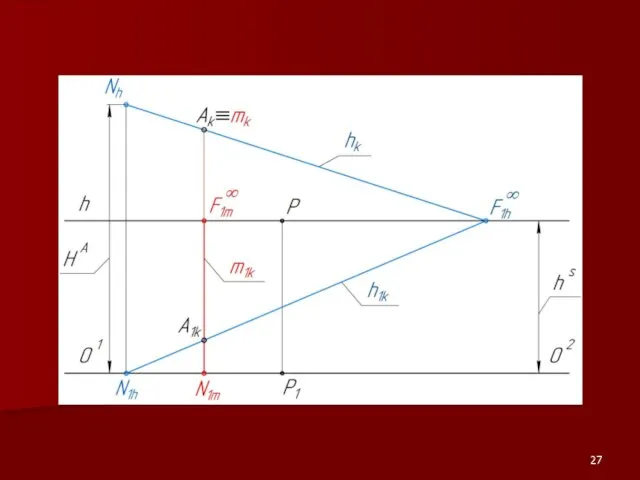
Если F∞k выше линии горизонта, то прямая восходящая.
Если F∞k ниже линии горизонта, то прямая нисходящая.
Если F∞k лежит на линии горизонта, т.е. F∞k ≡ F∞1k , то прямая
является горизонталью.
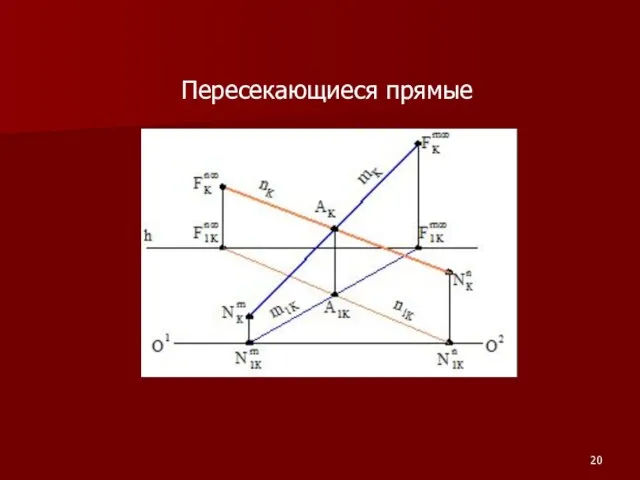
Слайд 19Взаимное положение прямых
Параллельные прямые

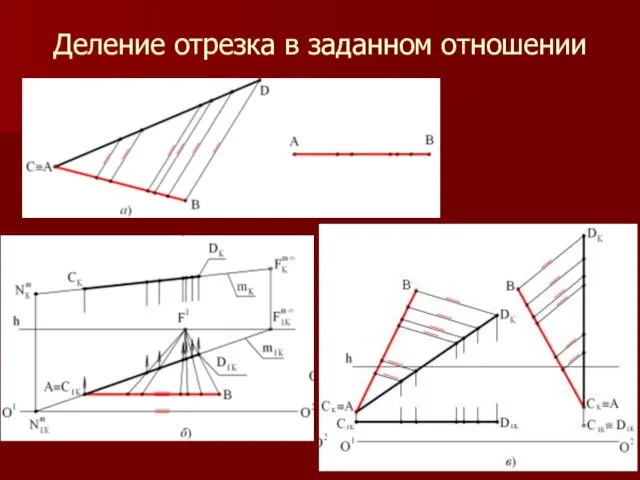
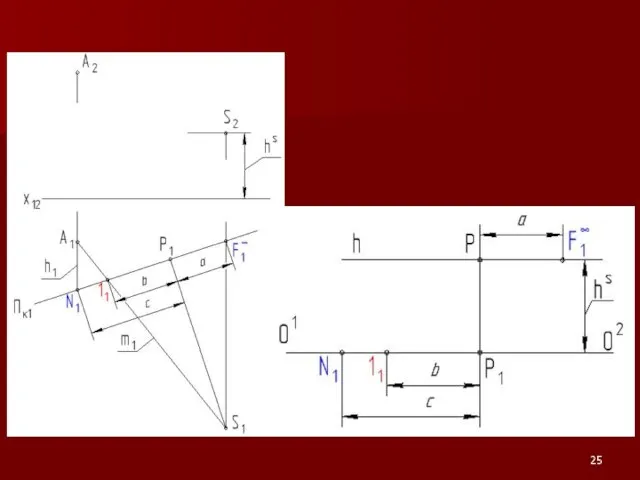
Слайд 21Деление отрезка в заданном отношении
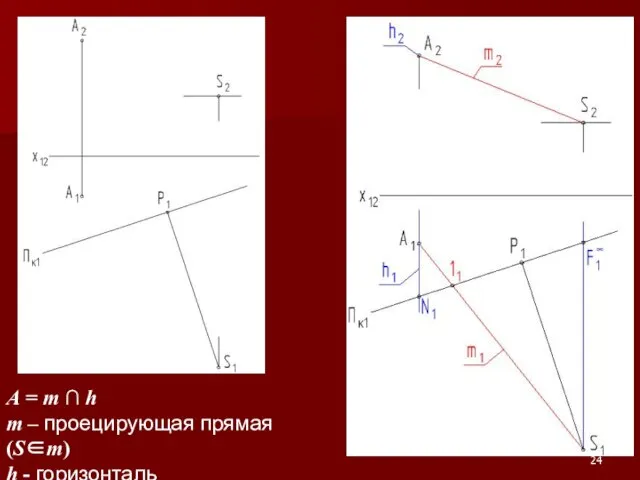
Слайд 23Каждая точка плана должна быть задана как точка пересечения двух прямых.

Слайд 24A = m ∩ h
m – проецирующая прямая (S∈m)
h - горизонталь
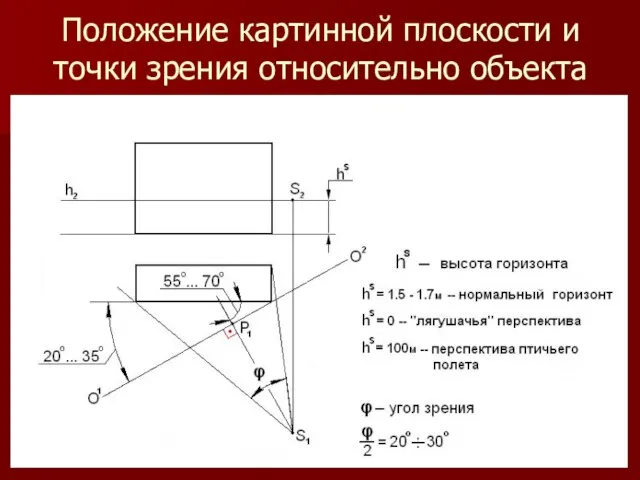
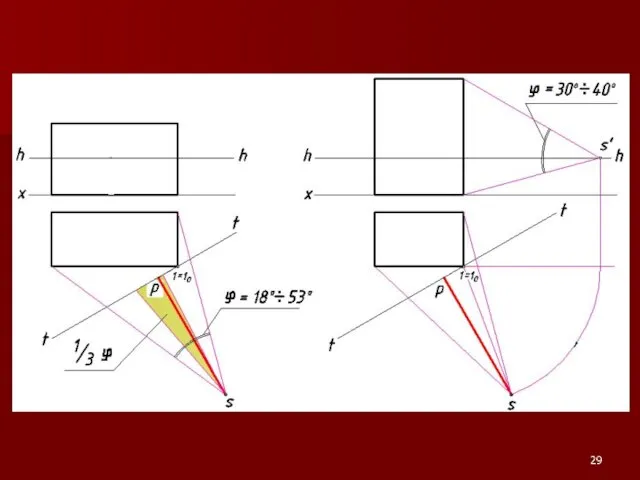
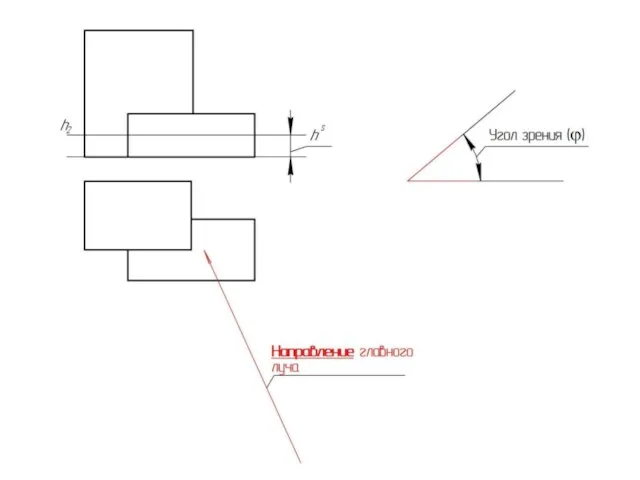
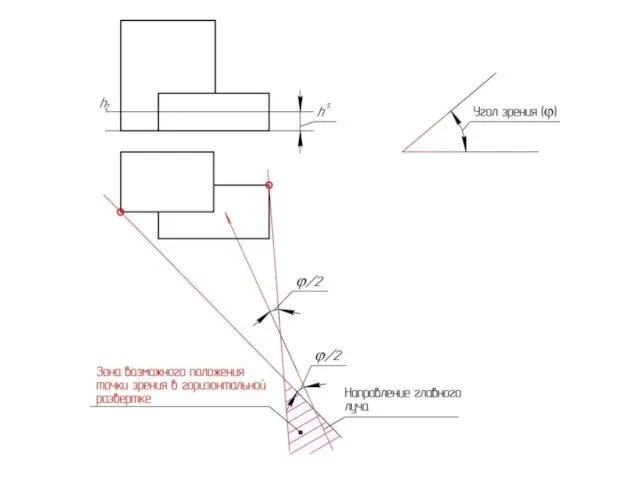
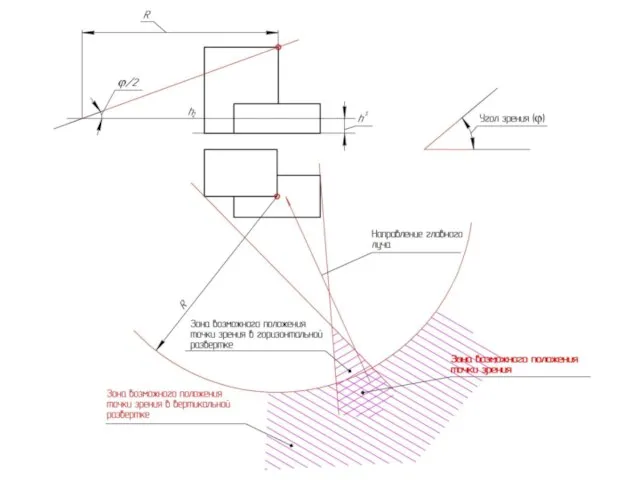
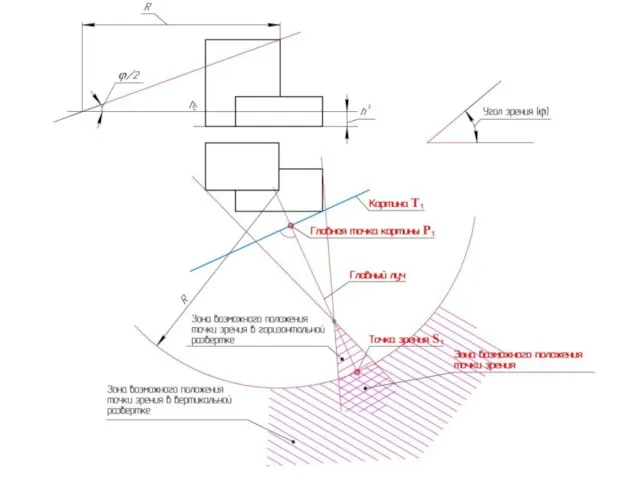
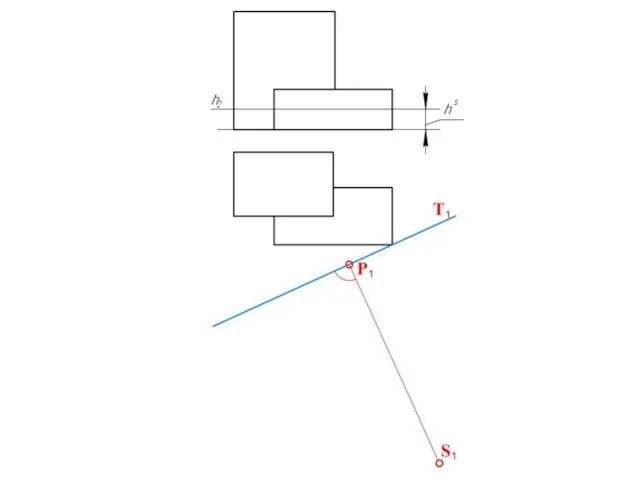
Слайд 28Положение картинной плоскости и точки зрения относительно объекта
Слайд 36Метод «архитекторов»
Данный метод построения линейной перспективы основан на использовании точек схода пучков

параллельных между собой прямых.
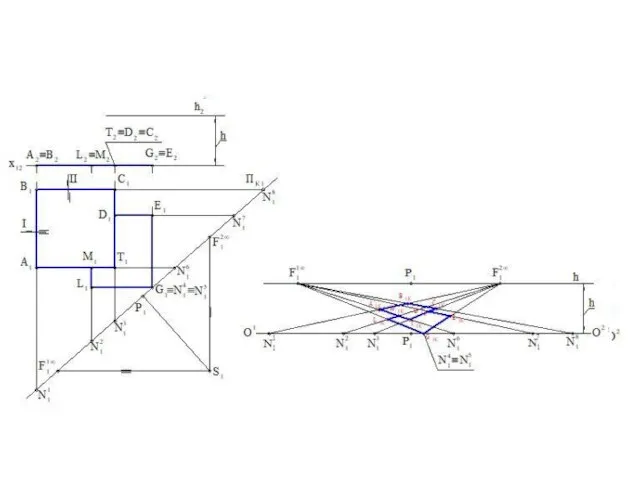
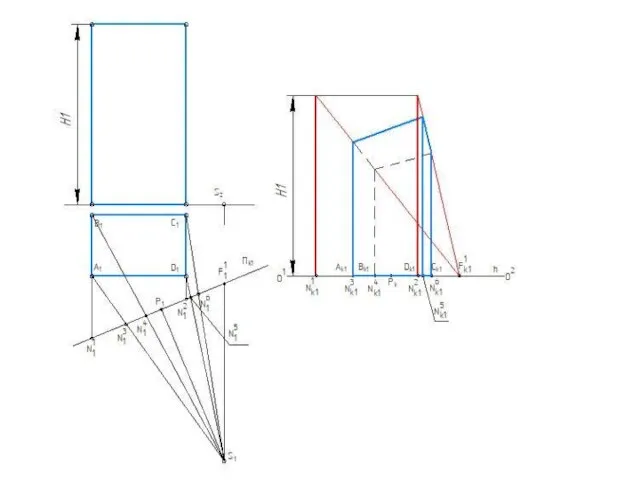
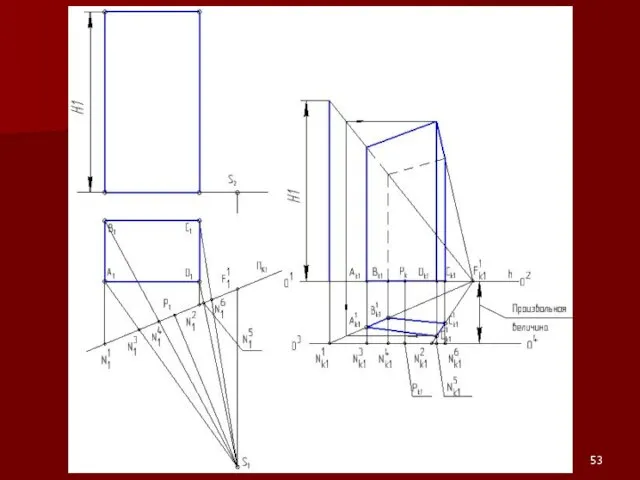
Слайд 52Использование одной точки схода
Опущенный план

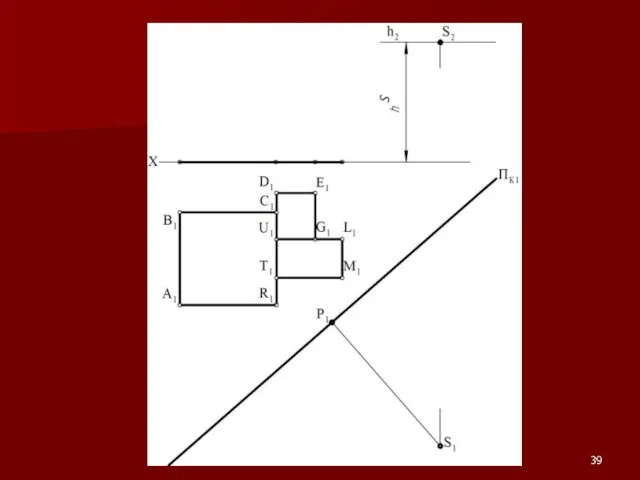
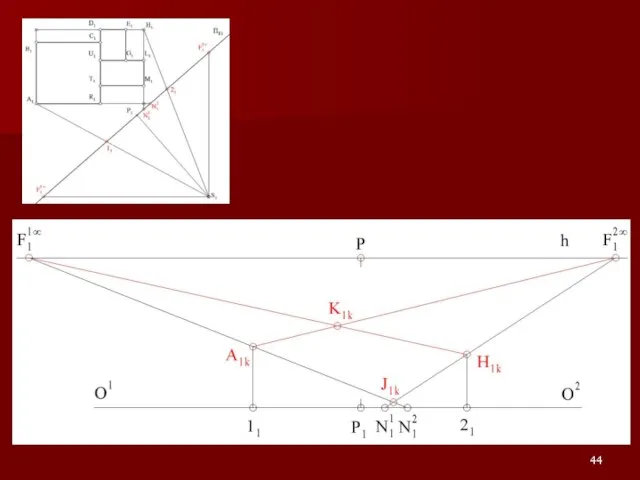
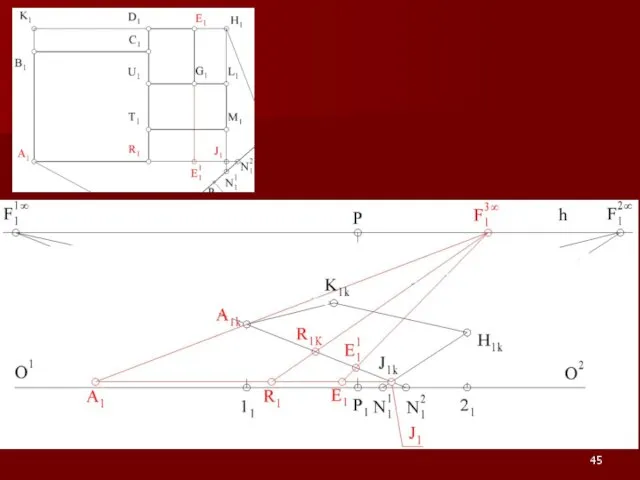
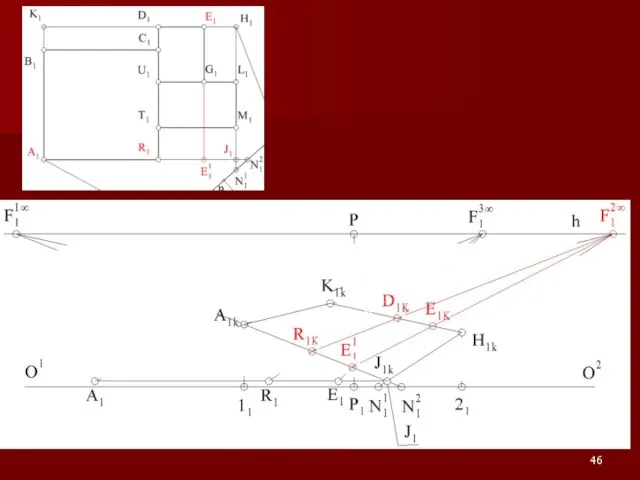
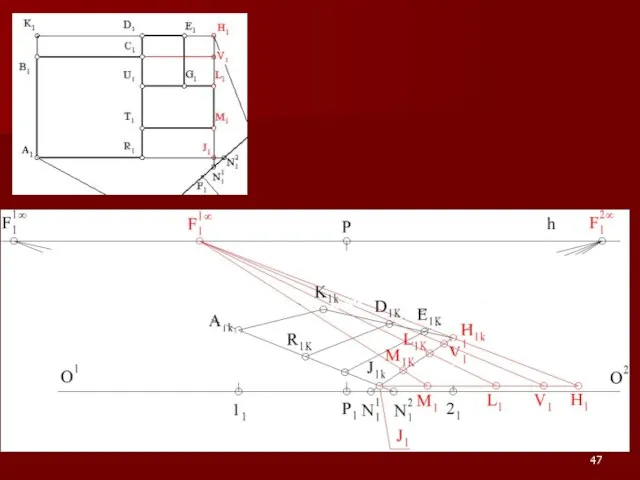
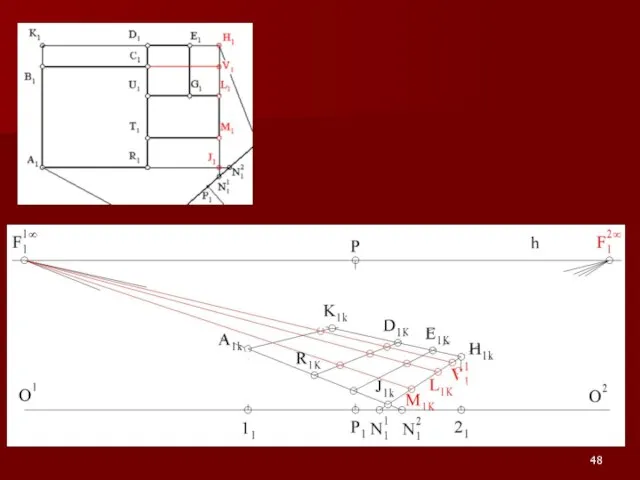
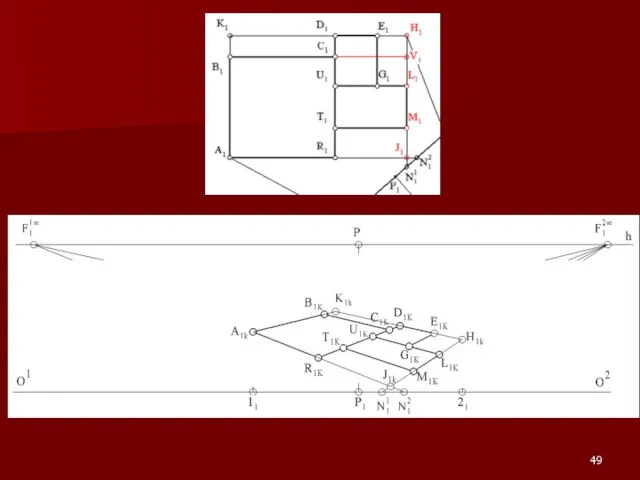
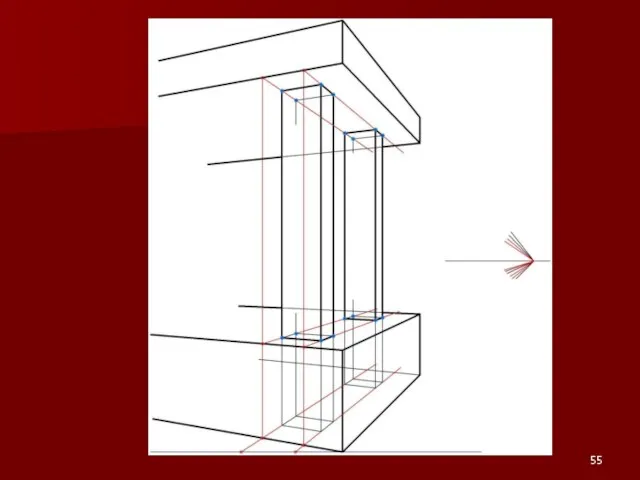
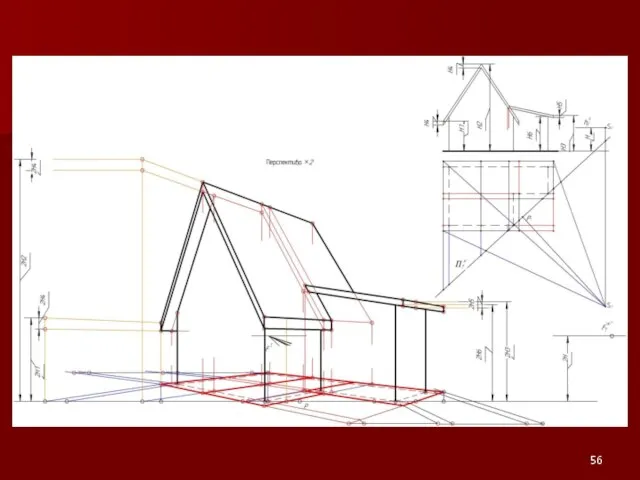
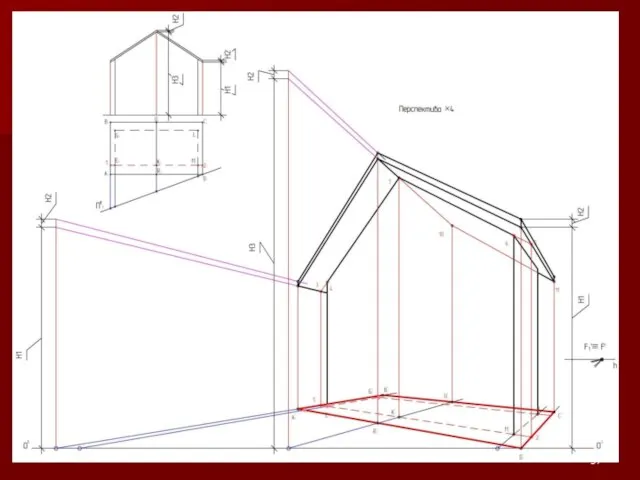
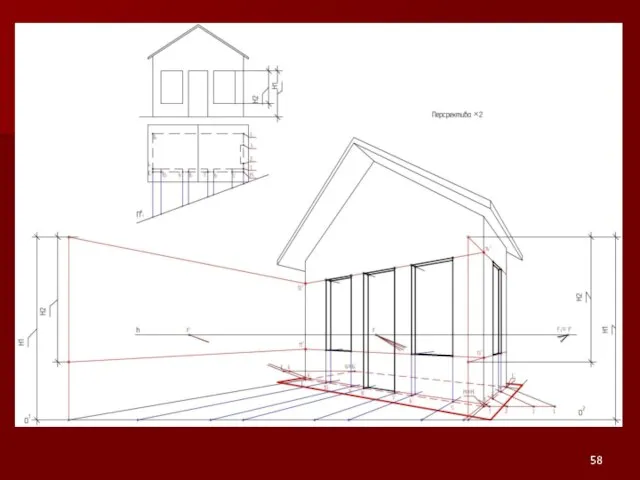
Слайд 54Примеры на построение перспективы























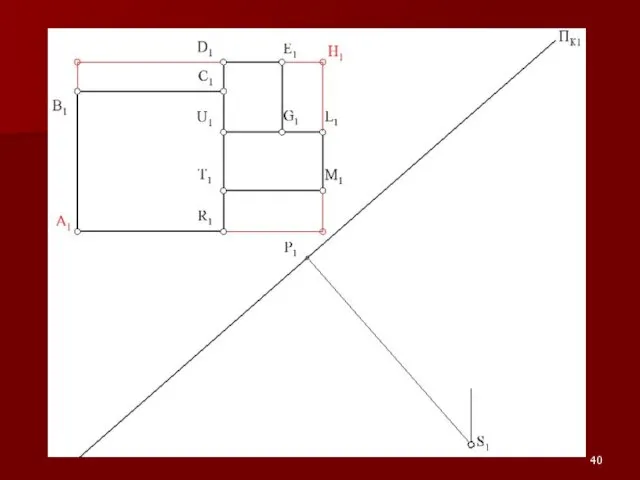
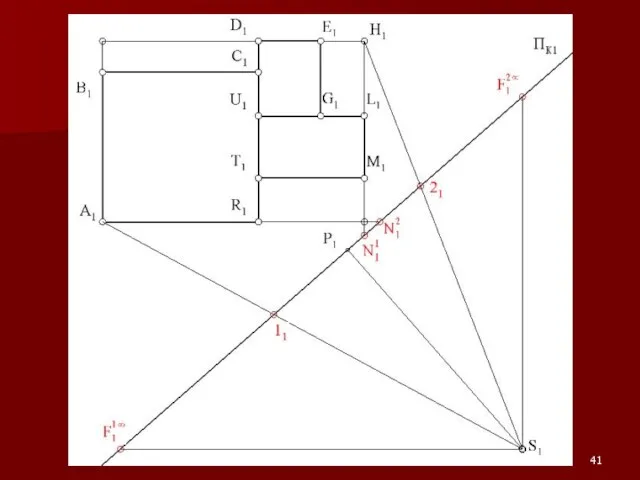
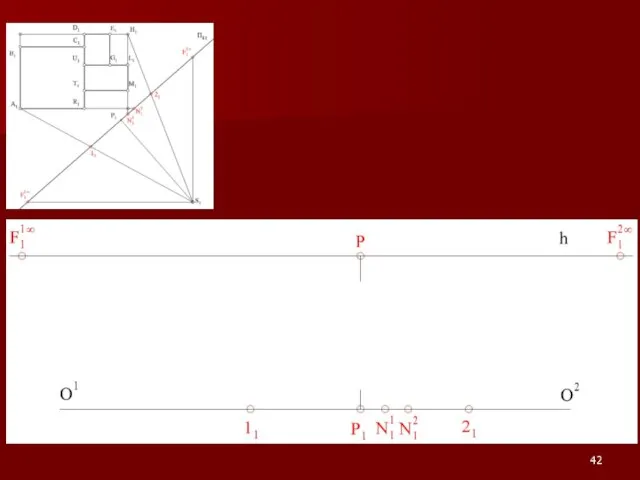
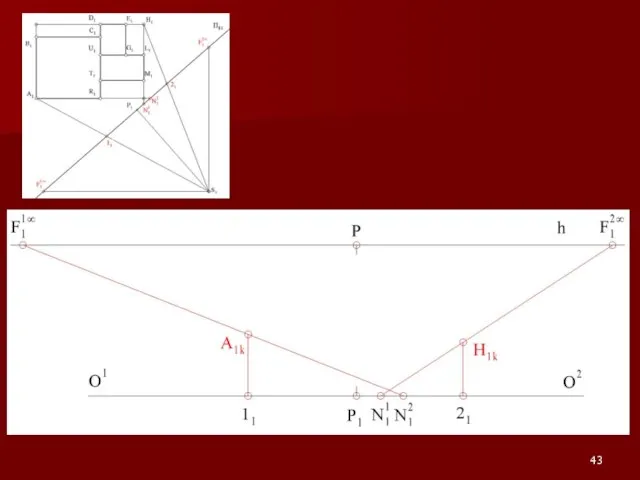



 Показатели качества деталей. Классификация показателей качества продукции. Определение номеклатуры показателей качества
Показатели качества деталей. Классификация показателей качества продукции. Определение номеклатуры показателей качества Кожа и ультрафиолетовые лучи
Кожа и ультрафиолетовые лучи Принципы, критерии и методы педагогического прогнозирования индивидуальной образовательной траектории
Принципы, критерии и методы педагогического прогнозирования индивидуальной образовательной траектории Студенческое самоуправление:основные мероприятия в 2011 г.
Студенческое самоуправление:основные мероприятия в 2011 г. Игры со шнуровкой
Игры со шнуровкой Графические объекты. Опорный конспект
Графические объекты. Опорный конспект Жизнь экосистемы. Биосфера и экосистема. Экологическая система
Жизнь экосистемы. Биосфера и экосистема. Экологическая система Руководство механики работы по проекту AUTO.RU
Руководство механики работы по проекту AUTO.RU Особенности энергосервисных контрактов в многоквартирных домах
Особенности энергосервисных контрактов в многоквартирных домах Презентация на тему Умножение и деление положительных и отрицательных чисел
Презентация на тему Умножение и деление положительных и отрицательных чисел Популяция (1)
Популяция (1) Конкурсный проект смотровой площадки на вершине горы Машук
Конкурсный проект смотровой площадки на вершине горы Машук Презентация на тему Рокоссовский Константин Константинович
Презентация на тему Рокоссовский Константин Константинович  Радианная мера углов и дуг
Радианная мера углов и дуг ДИАГРАММА «Моя квартира»
ДИАГРАММА «Моя квартира» Инфекционные осложнения после абортов
Инфекционные осложнения после абортов Гонка Чемпионов: Шумахер или Лёб? Тактика выживания бизнеса в кризис Сергей Петренко 1 апреля 2009 года. - презентация
Гонка Чемпионов: Шумахер или Лёб? Тактика выживания бизнеса в кризис Сергей Петренко 1 апреля 2009 года. - презентация Сведения о бетоне
Сведения о бетоне Право и государство
Право и государство За счет чего российские компании могут конкурировать глобально?
За счет чего российские компании могут конкурировать глобально? Cистема FATC1 климат-контроль
Cистема FATC1 климат-контроль "АНТИКРИЗИСНОЕ УПРАВЛЕНИЕ"
"АНТИКРИЗИСНОЕ УПРАВЛЕНИЕ" Александр Невский (7 класс)
Александр Невский (7 класс) Фонд обязательного медицинского страхования
Фонд обязательного медицинского страхования Ясенев Вячеслав Николаевич
Ясенев Вячеслав Николаевич Летний оздоровительный лагерь «МАЛЫШОК»
Летний оздоровительный лагерь «МАЛЫШОК» Программы сопровождения педагогических кадров Профессионал
Программы сопровождения педагогических кадров Профессионал Презентация на тему Антикоррупционная политика
Презентация на тему Антикоррупционная политика