Содержание
- 2. Содержание 1. Понятие логарифма. 2. Графики логарифмических функций. 3. Свойства логарифмов. 4. Решение логарифмических уравнений. 5.
- 3. Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в
- 4. В зависимости от значения основания приняты два обозначения Если основанием является 10, то вместо log10 x
- 5. Можно выделить три формулы Из определения логарифма следует следующее тождество: Примеры:
- 6. Графики логарифмических функции 1. y = lg x 2. y = ln x 3. y =
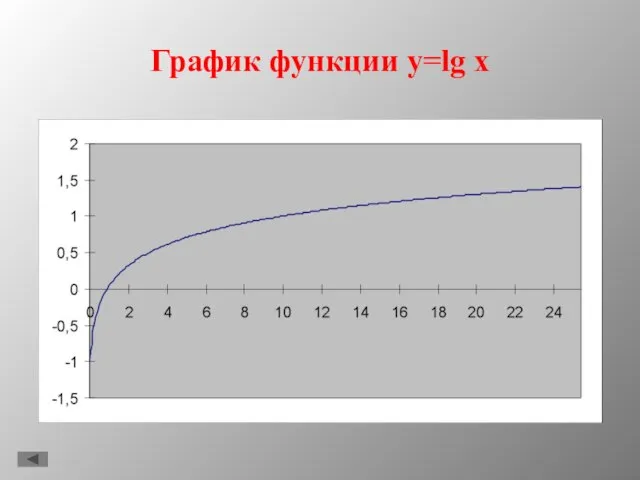
- 7. График функции y=lg x
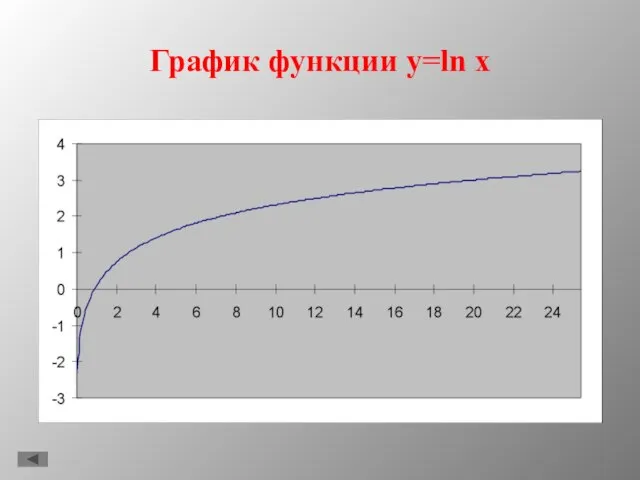
- 8. График функции y=ln x
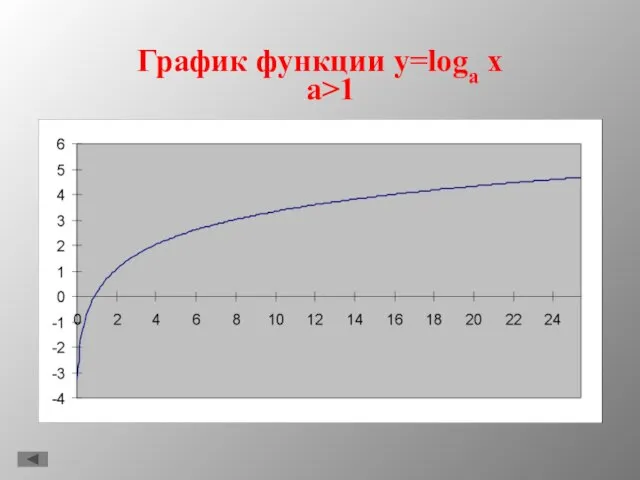
- 9. График функции y=loga x a>1
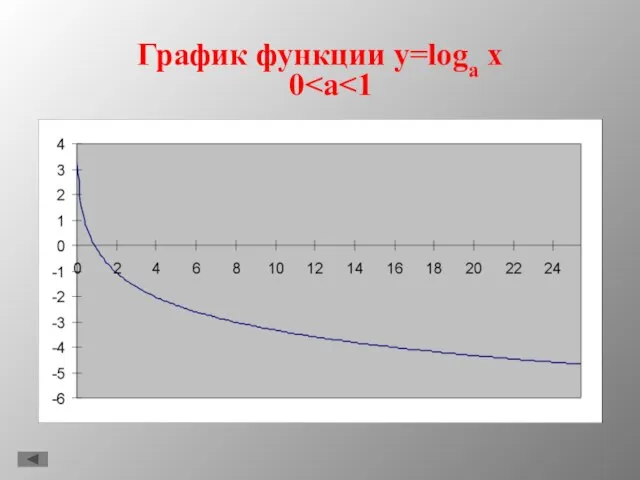
- 10. График функции y=loga x 0
- 11. Свойства f(x)=loga x D(f)=(0;+∞); Не является ни четной, ни нечетной; При a>1 функция возрастающая, при 0
- 12. Свойства логарифмов 1. Логарифм произведения. 2. Логарифм частного. 3. Логарифм степени. 4. Логарифм корня. 5. Переход
- 13. 1. Логарифм произведения равен сумме логарифмов множителей: 2. Логарифм частного равен логарифмов делимого без логарифма делителя:
- 14. 3. Логарифм степени равен произведению показателя степени на логарифм ее основания: 4. Логарифм корня равен отношению
- 15. 5. Переход от одного основания к другому
- 16. Свойства натуральных логарифмов Чтобы по известному десятичному логарифму числа х найти его натуральный логарифм, нужно разделить
- 17. Решения логарифмических уравнений
- 18. Решить уравнение: Значит,
- 19. Решение логарифмических неравенств
- 20. Решите неравенство:
- 22. Скачать презентацию

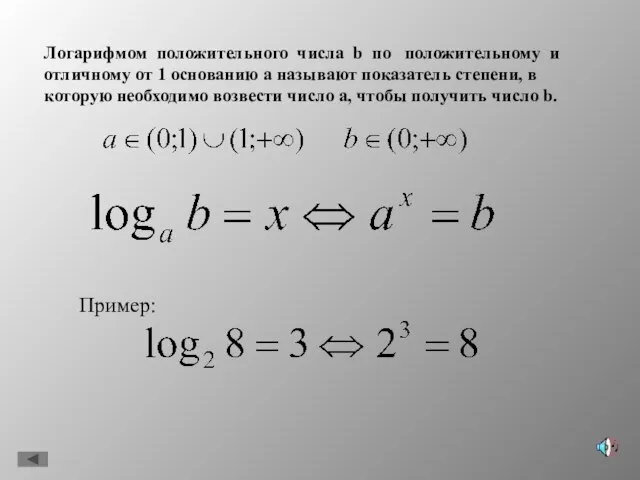





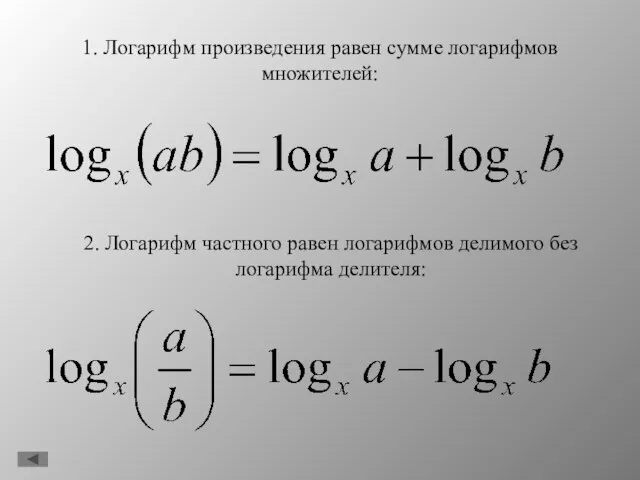







 Ход реализации пилотных проектов Росреестра на территории республики, а также создание региональной модели инфраструктуры прост
Ход реализации пилотных проектов Росреестра на территории республики, а также создание региональной модели инфраструктуры прост Пройдём с тобой по школьным этажам …
Пройдём с тобой по школьным этажам … Бал во дворце. Урок изобразительного искусства (5 класс)
Бал во дворце. Урок изобразительного искусства (5 класс) Биоинформатика
Биоинформатика Новоладожская детская школа искусств. Обучение детей росписи по ткани в технике холодного батика
Новоладожская детская школа искусств. Обучение детей росписи по ткани в технике холодного батика Кофейня «Blanco y negro»
Кофейня «Blanco y negro» ИНФОРМАЦИЯ О КОМПАНИИ
ИНФОРМАЦИЯ О КОМПАНИИ Презентация на тему Животный мир Арктики и Антарктиды
Презентация на тему Животный мир Арктики и Антарктиды  День полиции
День полиции Должностная инструкция
Должностная инструкция Подготовительные недели Великого Поста
Подготовительные недели Великого Поста Легко ли быть изобретателем?
Легко ли быть изобретателем? Итоговая аттестация выпускников старшей школы. ГОУСОШ №820
Итоговая аттестация выпускников старшей школы. ГОУСОШ №820 28-я Международная специализированная выставка Реклама 2021
28-я Международная специализированная выставка Реклама 2021 What are they wearing gtame
What are they wearing gtame Спешите стать терпимей и добрей
Спешите стать терпимей и добрей Презентация на тему Слово Предложение
Презентация на тему Слово Предложение Политическая система общества
Политическая система общества  Презентация на тему Любовная лирика Пушкина
Презентация на тему Любовная лирика Пушкина  «Алфавит - животные» (в загадках и картинках)
«Алфавит - животные» (в загадках и картинках) Палеозой
Палеозой Игра «Знатоки квадратных уравнений»
Игра «Знатоки квадратных уравнений» Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов
Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов дз
дз Риски информационной безопасности при передаче систем на аутсорсинг
Риски информационной безопасности при передаче систем на аутсорсинг Политический анализ
Политический анализ Штефан Кукс Stephan Kux Отдел Экономики Economic Development Кантон Цюрих Canton of Zurich
Штефан Кукс Stephan Kux Отдел Экономики Economic Development Кантон Цюрих Canton of Zurich  Стажировка в АО Сибур-Нефтехим (специалист планово-экономического отдела)
Стажировка в АО Сибур-Нефтехим (специалист планово-экономического отдела)