Логарифмические уравнения

Для чего были придуманы логарифмы?
Для ускорение вычислений.
Для упрощений вычислений.
Для решение астрономических задач.
В современной школе основной формой обучения математике ,главным связующем звеном в интеграции различных организационных форм обучения по-прежнему остается урок. В процессе обучения математический материал осознается и усваивается преимущественно в процессе решения задач, потому на уроках математики теория не изучается в отрыве от практики. Для того чтобы успешно решать логарифмические уравнения , на которые в учебном плане отведено всего 3 часа, необходимо уверенное владение формулами для логарифмов и свойствами логарифмической функции. Тема « Логарифмические уравнения» в учебном плане идет за логарифмическими функциями и свойствами логарифмов.
Ситуация несколько осложняется по сравнению с показательными уравнениями наличием ограничений на область определения логарифмических функций . Использования формул логарифма произведения, частного и других без дополнительных оговорок может привести как к приобретению посторонних корней, так и к потери корней . Поэтому необходимо внимательно следить за равносильностью совершаемых преобразований.

“Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»
Тема: « Логарифмические уравнения.»
Цели:
Образовательные:
1.Ознакомить и закрепить основные методы решения логарифмических уравнений, предупредить появления типичных ошибок.
2.Предоставить каждому обучающему возможность проверить свои знания и повысить их уровень.
3.Активизировать работу класса через разные формы работы.
Развивающие:
1.Развивать навыки самоконтроля.
Воспитательные:
1.Воспитывать ответственное отношение к труду.
2.Воспитывать волю и настойчивость , для достижение конечных результатов.

Урок №1.
Тема урока: «Методы решения логарифмических уравнений»
Тип урока: Урок ознакомления с новым материалом
Оборудование : Мультимедиа.
Ход урока.
1Организационный момент:
2.Актуализация опорных знаний;
Упростите:

Определение: Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.
Простейшим примером логарифмического уравнения служит уравнение
loga х = б (а > 0, а≠ 1, б>0 )
Способы решения
Решение уравнений на основании определения логарифма, например, уравнение loga х = б (а > 0, а≠ 1, б>0 ) имеет решение х = аb.
Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
если , loga f(х) = loga g(х), то f(х) = g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1.
Метод введение новой переменной.
Метод логарифмирования обеих частей уравнения.
Метод приведения логарифмов к одному и тому же основанию.
Функционально – графический метод.

1метод:
На основе определения логарифма решаются уравнения, в которых по данным основаниям и числу определяется логарифм, по данному логарифму и основанию определяется число и по данному числу и логарифму определяется основание.
Log2 4√2= х, log3√3 х = - 2 , logх 64= 3,
2х= 4√2, х =3√3 – 2 , х3 =64,
2х = 25/2 , х =3- 3 , х3 = 43 ,
х =5/2 . х = 1/27. х =4.

2метод:
Решите уравнения:
lg(х2-6х+9) - 2lg(х - 7) = lg9.
Условие для проверки всегда составляем по исходному уравнению.
(х2-6х+9) >0, х≠ 3,
Х-7 >0; х >7; х >7.
С начало нужно преобразовать уравнение привести к виду
log ((х-3)/(х-7))2 = lg9 применяя формулу логарифм частного.
((х-3)/(х-7))2 = 9,
(х-3)/(х-7) = 3, (х-3)/(х-7)= - 3 ,
х- 3 = 3х -21 , х -3 =- 3х +21,
х =9. х=6. посторонний корень.
Проверка показывает 9 корень уравнения. Ответ : 9

3 метод:
Решите уравнения:
log62 х + log6 х +14 = (√16 – х2)2 +х2,
16 – х2 ≥0 ; - 4≤ х ≤ 4;
х >0 , х >0, О.Д.З. [ 0,4).
log62 х + log6 х +14 = 16 – х2 +х2,
log62 х + log6 х -2 = 0
заменим log6 х = t
t 2 + t -2 =0 ; Д = 9 ; t1 =1 , t2 = -2.
log6 х = 1 , х = 6 посторонний корень .
log6 х = -2, х = 1/36 , проверка показывает 1/36 является корнем .
Ответ : 1/36.

4метод:
Решите уравнения
= ЗХ , возьмем от обеих частей уравнения логарифм по основанию 3
Вопрос :
1.Это – равносильное преобразования ?
2.Если да то почему ?
Получим
log3 = log3 (3х)
.
Учитывая теорему 3 , получаем : log3 х2 log3 х = log3 3х,
2log3 х log3 х = log3 3+ log3 х,
2 log32 х = log3 х +1,
2 log32 х - log3 х -1=0,
заменим log3 х = t , х >0 2 t 2 + t -2 =0 ; Д = 9 ; t1 =1 , t2 = -1/2
log3 х = 1 , х=3,
log3 х = -1/ 2 , х= 1/√3. Ответ: {3 ; 1/√3. }.

5 метод :
Решить уравнения: log9( 37-12х ) log7-2х 3 = 1,
37-12х >0, х< 37/12,
7-2х >0, х< 7/2, х< 7/2,
7-2х≠ 1; х≠ 3; х≠ 3;
log9( 37-12х ) / log3 (7-2х ) = 1,
½ log3( 37-12х ) = log3 (7-2х ) ,
log3( 37-12х ) = log3 (7-2х )2 ,
37-12х= 49 -28х +4х2 ,
4х2-16х +12 =0,
х2-4х +3 =0, Д=19, х1=1, х2=3, 3 –посторонний корень .
Проверкой убеждаемся , что х=1 корень уравнения.

6 метод
Решите уравнения: log3 х = 12-х.
Так как функция у= log3 х возрастающая , а функция у =12-х убывающая на (0; + ∞ ) то заданное уравнение на этом интервале имеет один корень. Который легко можно найти. При х=10 заданное уравнение обращается в верное числовое равенство 1=1. Ответ х=10.

Итог урока.
С какими методами решения логарифмических уравнений мы познакомились на уроке? Домашние задание:
Определите метод решения и решите № 1547(а,б) ,№1549(а,б), №1554(а,б) .
Проработать весь теоретический материал и разобрать примеры §52.

2 урок.
Тема урока: «Применение различных методов при решение логарифмических уравнений.»
Тип урока: Урок закрепления изученного
Ход урока.
1.Организационный момент:
2.«Проверь себя»
1)log-3 ((х-1)/5)=?
2) log5 (121 – x2), (121 – x2) ≥ 0, x < – 11, x ≥ 11.
3) 32х =5, log5 3=2х , х = (log5 3)/2.
2log3 5 4log3 5
4) 9 =3 = 45
5) lg x2 = 2lg x.

3.Выполнение упражнений:
№1563 (б )
Каким способом можно решить данное уравнение ? (метод введение новой переменной )
log3 2х +3 log3х +9 = 37/ log3 (х/27); х>0
Обозначим log3х = t ; t 2 -3 t +9 =37/(t-3) ; t ≠ 3,
(t-3) ( t 2 -3 t +9) = 37,
t3-27 = 37; t3= 64 ; t=4.
log3х = 4 ; х= 81.
Проверкой убеждаемся , что х=81 корень уравнения.

№1564 (а);(метод логарифмирования )
log3 х
Х = 81 , возьмем от обеих частей уравнения логарифм по основанию 3;
log3 х
log3 Х = log3 81; log3х log3х = log381; log3 2х =4;
log3х =2, х=9 ;
log3 х = -2, х=1/9.
Проверкой убеждаемся , что х=9 и х=1/9 корни уравнения.

4.Физкультминутка(за партами , сидя ).
1 Областью определения логарифмической функции у= log3 Х является множество положительных чисел .
2Функция у= log3 Х монотонно возрастает .
3.Область значений логарифмической функции от 0 до бесконечности.
4 logас/в = logа с - logа в.
5 Верно ,что log8 8-3 =1.

№1704.( а)
1-√х =In х
Так как функция у= In х возрастающая , а функция
у =1-√х убывающая на (0; + ∞ ) то заданное уравнение на этом интервале имеет один корень. Который легко можно найти. При х=1 заданное уравнение обращается в верное числовое равенство 1=1.
Ответ : х=1.

№ 1574(б)
log3 (х+2у) -2log3 4 =1- log3 (х – 2у), log3 (х 2 - 4у 2) = log3 48,
log1/4 (х -2у) = -1; log1/4 (х -2у) = -1;
х 2 - 4у 2 – 48 =0, х =4 +2у, х =8,
х -2у = 4; 16у = 32; у =2.
Проверкой убеждаемся, что найденное значения является решениями системы.

5. Что за прелесть Логарифмическая “комедия 2 > 3”
1/4 > 1/8, бесспорно правильно.
(1/2)2 > (1/2)3, тоже не внушающее
сомнение. Большему числу соответствует больший логарифм,
значит,
lg(1/2)2 > lg(1/2)3; 2lg(1/2) > 3lg(1/2). После сокращения на
lg(1/2) имеем
2 > 3.
- Где ошибка?

6.Выполните тест:
1Найдите областью определения: у = log0,3 (6х –х2 ).
1(-∞ ;0) Ư(6 ; + ∞ ); 2. (-∞ ; -6) Ư(0 ; + ∞ ); 3.(-6; 0 ). 4.(0; 6 ).
2.Найдите область значений : у =2,5 + log1,7 х.
1(2,5 ; + ∞ ); 2. (-∞ ; 2,5); 3 (- ∞ ; + ∞ ); 4. (0 ; + ∞ ).
3.Сравните : log0,5 7 и log0,5 5.
1.>. 2.<. 3.=.
4. Решите уравнение : 7 *5 log5 X = х +21.
1.( 3,5 ). 2. нет решения. 3.( – 3,5) . 4.( 7).
5. Найти значение выражения : log4 (64с) если log4 с = -3,5.
1. ( -6,5 ) . 2. (- 0, 5 ) 3. (- 10, 5 ) 4.( -67,5).

Ответ: 4; 3;2;1;2.
Итог урока: Чтобы хорошо решать
логарифмические уравнения , нужно
совершенствовать навыки решения
практических заданий ,так как они являются
основным содержанием экзамена и жизни.
Домашние задания : № 1563(а,б), №1464(б,в) , № 1567 (б).

Урок 3.
Тема урока: «Решение логарифмических уравнений »
Тип урока: урок обобщения, систематизация знаний.
Ход урока.
1.Актуализация опорных знаний:
№1 Какие из чисел -1; 0; 1; 2; 4; 8 являются корнями уравнения log2 х=х-2?
№2 Решить уравнения: а) log16х= 2; в) log2 (2х- х2 ) -=0;
г) log3 (х-1)=log3 (2х+1)
№3 Решить неравенства: а) log3 х> log3 5; б) log0,4 х< 1;
в) log2 (х-4) >0 .
№4 Найдите область определения функции: у = log2 (х+4)
№5 Сравните числа: log3 6/5 и log3 5/6; log0,2 5 и . Log0,2 17.
№6 Определить число корней уравнения: log3 Х= =-2х+4.

2. Решение уравнений:
1. решите уравнения: log5 2 (х-3)2 +3 log5 (15 -5х ) -10 = 0.
ОДЗ: 15 -5х>0 , х<3.
Log5 2 (х-3)2 +3 log5 (5 (3 -х )) -10 =0,
(2 log5 (х-3))2 +3 log2 (3 -х ) +3 -10 = 0, 4 log5 2 (3-х)2 +3 log2 (3 -х ) -7= 0,
Пусть log5(3-х) = t; 4 t 2 -3 t -7 =0,
t =-7/4 ; t=1 .
log5(3-х) = -7/4, и log5(3-х) = 1,
3-х =5-7/4 , 3-х =5,
х =3 -1/57/4. х = - 2.
Ответ: { 3 -1/57/4 ; -2}.

Решите уравнения: 3log4 (2+ 30/(2х-11)) = 2log4 (2 – 15/(х+2)) + 8 .
2+ 30/(2х-11)= (4х-22+30)/(2х-11)=(4х+8)/(2х-11)=4(х+2)/(2х-11)
2 – 15/(х+2)=(2х+4-15)/(2+х)=(2х-11)/(х+2)=((х+2)/(2х-11))-1,
3 log4 (4(х+2)/(2х-11)) = 2log4 ( (х+2)/(2х-11))-1+8 ,
3+3 log4 ((х+2)/(2х-11)) = - 2log4 ( (х+2)/(2х-11))+8 ,
Пусть log4 ((х+2)/(2х-11)) = t, 3+3t = -2 t +8, t = 1.
log4 ((х+2)/(2х-11)) =1, (х+2)/(2х-11) =4,
х+2=8х-44, х=46/7. Проверкой убеждаемся , что х=46/7 корень уравнения.

3.Физкультминутка:
1. 3 log38 = 8.
2. lg х= - 2 , решением данного уравнения является 100.
3 Функция у= log4/3 Х монотонно возрастает .
4. logа (х+у) = logа х + logа у.
5. logа (х+у) == logа х - logа у.
6. logа (ху) = logа х + logа у.

4.Учимся на чужих ошибках :
Воспользуемся формулой преобразования суммы логарифмов логарифм произведения. Получим уравнения log3 (х – 1) (х -3 ) = 1, отсюда следует
х2 – 4х + 3 =3.
Корнями последнего уравнения являются х1 =0 и х2 = 4,
Ответ : {0 , 4}.
Решите уравнения: log3 (х – 1) + log3 (х -3 ) = 1.

Решите уравнения log2 (х +1) - log2 (х -2 ) = 2.
Воспользуемся формулой преобразования разности логарифмов логарифм частного, получаем log2 (х +1) /(х- 2) = 2, откуда следует (х +1) /(х- 2) = 2.
Решив последнее уравнения ,находим х = 5.
Ответ: х = 5.

.
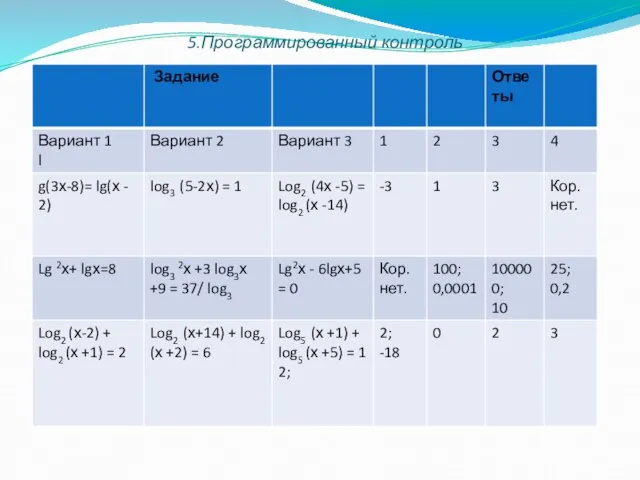
5.Программированный контроль
Решить уравнен