Сокращение дробей

Что произойдёт с величиной дроби при увеличении её числителя в несколько раз?
Вывод: Если Числитель дроби увеличить в несколько раз, не изменяя знаменателя, то дробь увеличится во столько же раз.
0

Что происходит с величиной дроби при уменьшении её числителя в несколько раз?
Вывод: Если числитель дроби
уменьшить в несколько раз,
не изменяя знаменателя,
то дробь уменьшится
во столько же раз.

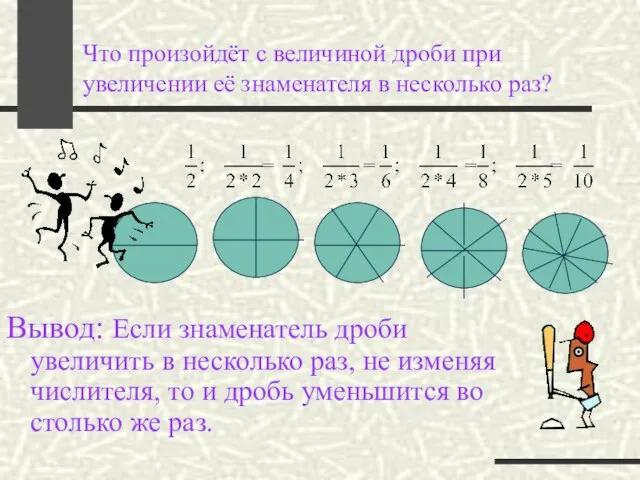
Что произойдёт с величиной дроби при увеличении её знаменателя в несколько раз?
Вывод: Если знаменатель дроби увеличить в несколько раз, не изменяя числителя, то и дробь уменьшится во столько же раз.
=
=
=
=

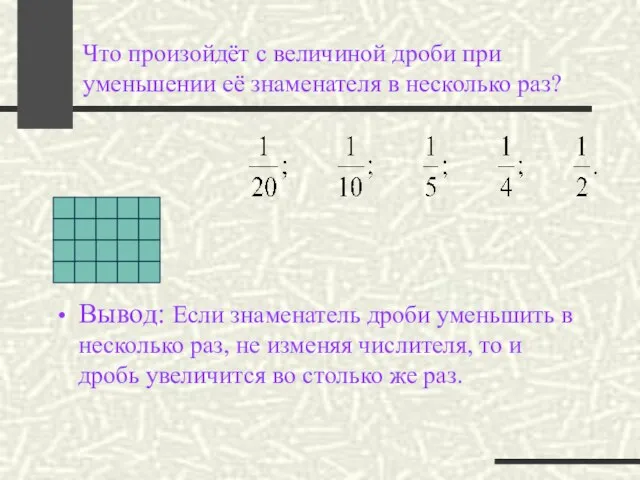
Что произойдёт с величиной дроби при уменьшении её знаменателя в несколько раз?
Вывод: Если знаменатель дроби уменьшить в несколько раз, не изменяя числителя, то и дробь увеличится во столько же раз.

А что произойдёт с величиной дроби при одновременном увеличении или уменьшении числителя и знаменателя в одно и то же число раз ?
Если числитель и знаменатель
дроби увеличить в одинаковое
число раз, то дробь не изменится.
.
???
Если числитель и знаменатель
Дроби уменьшить в одинаковое
Число раз, то дробь не изменится.

Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
аn
вп
=
а
в
а:m
в:m
=
а
в
.,

ВЕРНО ЛИ РАВЕНСТВО:

а) На каком свойстве основано сокращение дробей?
б) Какая дробь называется несократимой? в) Что меняется при сокращении дроби?

Сократите дробь:
Найдите сумму дробей и сократите результат:

Сократите неправильную дробь, и затем выделите из нее целую часть:
Какую часть прямого угла составляет угол, равный:
а) 36 см.; б) 75 см.; в) 40: см.

СОКРАТИТЕ ДРОБНОЕ ВЫРАЖЕНИЕ: