Содержание
- 2. Введение Изучение многих физических процессов и геометрических закономерностей часто приводит к решению уравнений, содержащих параметр. Решение
- 3. Анализ ситуации Логарифмы, а тем более с параметрами – вещь очень сложная. Поэтому перед началом проекта
- 4. Результаты опроса
- 5. Как мы видим из результатов опроса, логарифмические уравнения с параметрами особой популярностью не пользуются. Но это
- 6. Определение логарифма Логарифмом положительного числа в по основанию а, где а>0,a≠1,называется показатель степени c, в которую
- 7. Основное логарифмическое тождество =
- 8. Свойства логарифмов Пусть а>0, a=1, b>0, c>0, r, p- любые действительные числа.
- 9. Параметры С логарифмами и его свойствами разобрались, теперь приступим к параметрам. Определение: Параметрами называются переменные a,
- 10. Виды логарифмических уравнений с параметрами Логарифмические уравнения с параметрами можно разделить на три вида в зависимости
- 11. Уравнения, содержащие параметры в логарифмируемом выражении Решить при всех a: logx + 1(x2 + a) =
- 12. Уравнения, содержащие параметры в основании Решить при всех а: loga(x2+2x-8)=2 Решение: Из определения логарифма следует, что
- 13. Уравнения, содержащие параметры и в основании и в логарифмируемом выражении Решить при всех a уравнение loga(ax
- 14. Что дал этот проект? В процессе работы мы овладели начальными навыками решений параметрических уравнений, научились решать
- 15. Результаты повторного опроса По окончанию данного проекта был проведен повторный опрос на тему «Можете ли вы
- 17. Скачать презентацию





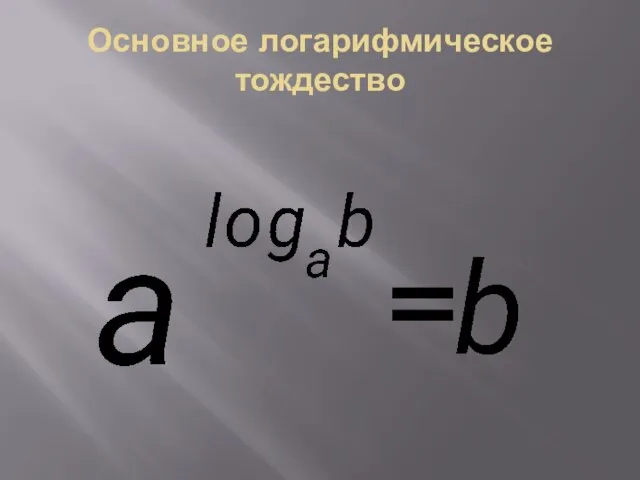








 Почему я тебя люблю и готова прожить с тобой всю жизнь
Почему я тебя люблю и готова прожить с тобой всю жизнь p1581509855
p1581509855 Презентация на тему Лицевая и изнаночная сторона тканей
Презентация на тему Лицевая и изнаночная сторона тканей квартет
квартет Фитнес между делом !
Фитнес между делом ! Презентация на тему Законы преломления
Презентация на тему Законы преломления  Завод по производству кофе
Завод по производству кофе How to celebrate the new year in spain
How to celebrate the new year in spain Фотоимпрессионизм. Пикториальная фотография
Фотоимпрессионизм. Пикториальная фотография Кластерное обследование по многим показателям-МИКС (4 раунд) Ключевые результаты МИКС- 2010/2011 в Казахстане
Кластерное обследование по многим показателям-МИКС (4 раунд) Ключевые результаты МИКС- 2010/2011 в Казахстане АЛКОГОЛИЗМ!
АЛКОГОЛИЗМ! Реализация ВФСК ГТО в образовательной организации ГАУ ДПО Саратовский областной институт развития образования
Реализация ВФСК ГТО в образовательной организации ГАУ ДПО Саратовский областной институт развития образования Обзор православной литературы Доброе слово для малых ребят
Обзор православной литературы Доброе слово для малых ребят ПредставляемОригинальные препараты цветочной терапии Баха- ЦВЕТЫ БАХА
ПредставляемОригинальные препараты цветочной терапии Баха- ЦВЕТЫ БАХА история избирательной системы в России
история избирательной системы в России П.И.Чайковский «Письмо миру»
П.И.Чайковский «Письмо миру» Признаки норм поведения
Признаки норм поведения Ортопедические матрасы. Долгожданная коллекция от Askona
Ортопедические матрасы. Долгожданная коллекция от Askona КиК – Безопасность, созданная в России
КиК – Безопасность, созданная в России Загробная жизнь в Древнем Египте: гробницы и саркофаги.
Загробная жизнь в Древнем Египте: гробницы и саркофаги. Презентация на тему Что изучает современная экология?
Презентация на тему Что изучает современная экология?  Отчет об исполнении сметы доходов и расходов Финакадемии за 2009 год
Отчет об исполнении сметы доходов и расходов Финакадемии за 2009 год Компьютер как формальный исполнитель алгоритмов
Компьютер как формальный исполнитель алгоритмов Презентация на тему Скульптура классицизма
Презентация на тему Скульптура классицизма Презентация без названия(1)
Презентация без названия(1) Презентация на тему Квантовая механика
Презентация на тему Квантовая механика PHRASEOLOGICAL UNITS IN ENGLISH
PHRASEOLOGICAL UNITS IN ENGLISH How to Jump Start a Car
How to Jump Start a Car