Содержание
- 2. Дискретные электронные устройства (ДЭУ) предназначены для приёма, преобразования и передачи электрических сигналов, полученных путём квантования по
- 3. Электрическим импульсом наз. кратковременное периодически повторяющееся отклонение напряжения u(t) или тока i(t) от установившегося значения. Перепадами
- 6. Импульсные электронные устройства (ИЭУ) реализуют квантование исходного сигнала х(t) по времени и преобразуют его в последовательность
- 7. а — изменение исходной аналоговой величины; б — последовательность амплнтудно-модулирояаияых b - импульсов: в — последовательность
- 8. Квантование исходного сигнала х(t) по времени (импульсные устройства) Квантование исходного сигнала х(t) по уровню (релейные устройства)
- 9. Цифровые электронные устройства (ЦЭУ) реализуют квантование исходного сигнала х(/) как по времени, так и по величине.
- 10. Релейные электронные устройства (РЭУ) реализуют квантование исходного сигнала x(t) по уровню и Преобразуют его в ступенчатую
- 11. Достоинства ЦЭУ: высокая помехоустойчивость; высокая на дежность; возможность длительного хранения информации без ее потери; экономическая эффективность,
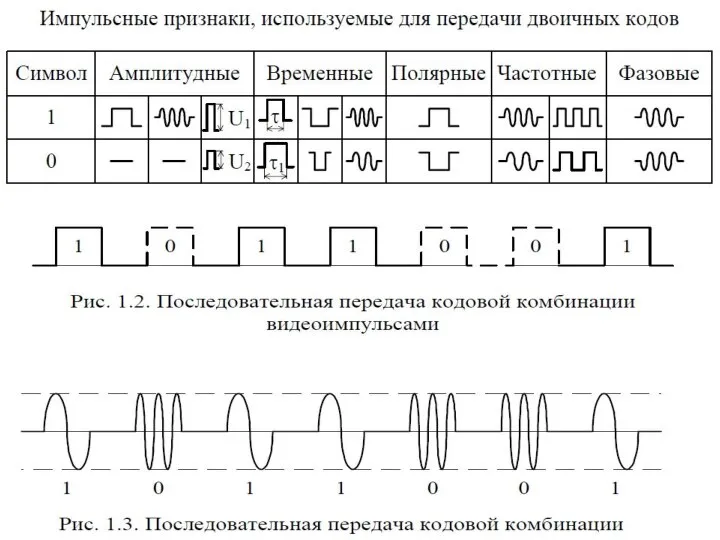
- 12. Цифровыми наз. устройства формирования, преобразования и передачи кодовых слов. Кодом наз. систему символов представления информации, удобную
- 13. Цифровые методы передачи информации по сравнению с другими имеют ряд преимуществ. Главными из них являются следующие:
- 14. Существующие системы счисления подразделяются на позиционные и непозиционные. В непозиционных системах значение конкретной цифры постоянно у
- 15. Количество различных чисел, которое может быть записано в позиционной системе счисления с основанием q при заданном
- 16. 1110110011
- 17. Число символов в кодовом слове цифрового устройства фиксировано, т.е. кодовые слова имеют одинаковую длину. Если кодовое
- 18. Переход от системы счисления с большим основанием к системе счисления с меньшим основанием выполняется с соблюдением
- 19. В качестве математического аппарата для функций и аргументов, принимающих только два значения — 0 и 1,
- 23. Самые современные и мощные микропроцессоры (компьютеры) из перечня арифметических операций способны выполнять только операцию сложения, то
- 24. Операции над кодовыми словами, представленными в виде электрических сигналов, в цифровом устройстве могут выполняться следующими двумя
- 25. последовательное (поразрядное, побитовое) выполнение операций параллельное выполнение операций последовательный ввод и параллельный вывод Параллельный ввод и
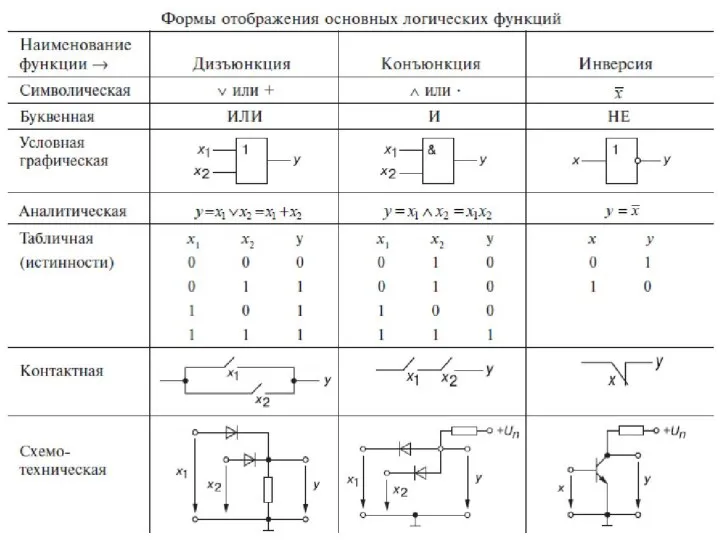
- 27. Логический элемент ИЛИ моделирует операцию логического сложения, или, как ее еще называют, операцию дизъюнкции. Алгебраически эта
- 28. Логический элемент И выполняет операцию логического умножения, или конъюнкции. Алгебраически эта операция записывается следующим образом: С=А*В
- 29. Логический элемент НЕ выполняет операцию отрицания, или | инверсии, алгебраически она записывается следующим образом: I С=А,
- 30. Функция "И" равна единице, если равны единице ВСЕ ее аргументы. Функция "ИЛИ" равна единице, если равен
- 31. Булевые (переключательные) функции бывают комбинационными и временными. Комбинационными наз. функции, значение которых однозначно определяется значениями их
- 33. Скачать презентацию
Слайд 2Дискретные электронные устройства (ДЭУ) предназначены для приёма, преобразования и передачи электрических сигналов,
Дискретные электронные устройства (ДЭУ) предназначены для приёма, преобразования и передачи электрических сигналов,

Действующие в них сигналы пропорциональны конечному числу выбранных по определённому закону значений реальной физической величины, отображаемой в виде различных параметров импульсов или перепадов сигнала, но так как информация о её изменении может быть получена только при сравнении двух импульсов, полу- нс такой информации растягивается во времени. Следовательно,, для получения полной информации о конечном во времени физическом процессе необходимо бесконечное число импульсов, т. е. временные масштабы протекания физического процесса и его отображения при помощи импульсов не совпадают. Поэтому в ДЭУ используется только часть информации о реальной физической величине, т. е. процесс представления информации сопряжён с частичной ее потерей.
Квантованием наз. процесс замены непрерывного сигнала его дискретными значениями в отдельных точках
Слайд 3Электрическим импульсом наз. кратковременное периодически повторяющееся отклонение напряжения u(t) или тока i(t)
Электрическим импульсом наз. кратковременное периодически повторяющееся отклонение напряжения u(t) или тока i(t)
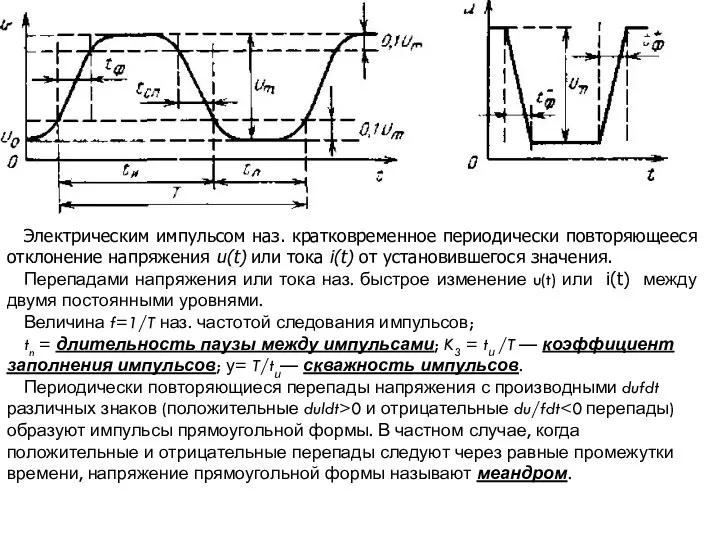
Перепадами напряжения или тока наз. быстрое изменение u(t) или i(t) между двумя постоянными уровнями.
Величина f=1/T наз. частотой следования импульсов;
tn = длительность паузы между импульсами; K3 = tи /T — коэффициент заполнения импульсов; у= T/tи— скважность импульсов.
Периодически повторяющиеся перепады напряжения с производными dufdt различных знаков (положительные duldt>0 и отрицательные du/fdt<0 перепады) образуют импульсы прямоугольной формы. В частном случае, когда положительные и отрицательные перепады следуют через равные промежутки времени, напряжение прямоугольной формы называют меандром.
Слайд 6Импульсные электронные устройства (ИЭУ) реализуют квантование исходного сигнала х(t) по времени и
Импульсные электронные устройства (ИЭУ) реализуют квантование исходного сигнала х(t) по времени и
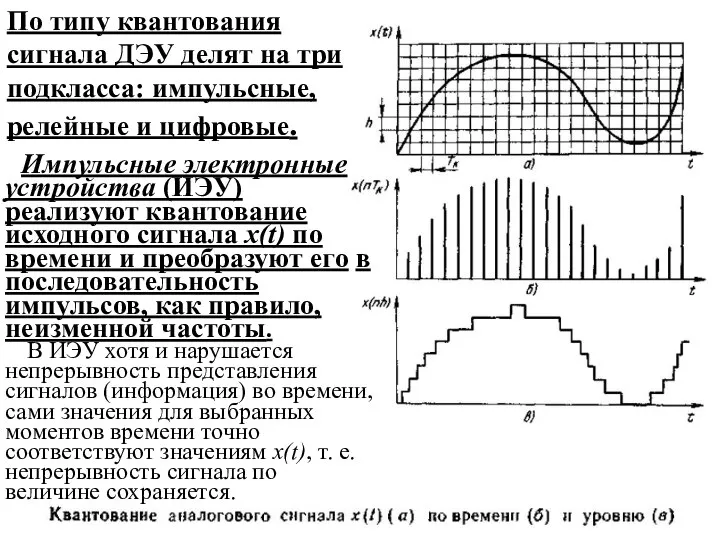
В ИЭУ хотя и нарушается непрерывность представления сигналов (информация) во времени, сами значения для выбранных моментов времени точно соответствуют значениям х(t), т. е. непрерывность сигнала по величине сохраняется.
По типу квантования сигнала ДЭУ делят на три подкласса: импульсные, релейные и цифровые.
Слайд 7а — изменение исходной аналоговой величины; б — последовательность амплнтудно-модулирояаияых b -
а — изменение исходной аналоговой величины; б — последовательность амплнтудно-модулирояаияых b -
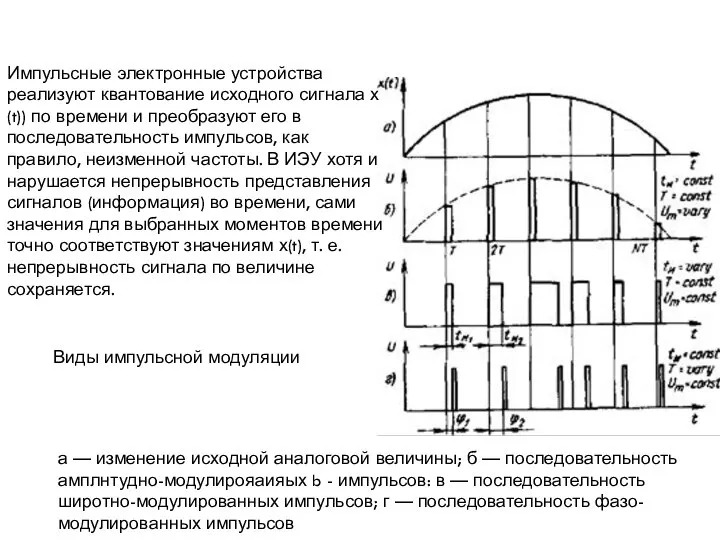
Виды импульсной модуляции
Импульсные электронные устройства реализуют квантование исходного сигнала х(t)) по времени и преобразуют его в последовательность импульсов, как правило, неизменной частоты. В ИЭУ хотя и нарушается непрерывность представления сигналов (информация) во времени, сами значения для выбранных моментов времени точно соответствуют значениям х(t), т. е. непрерывность сигнала по величине сохраняется.
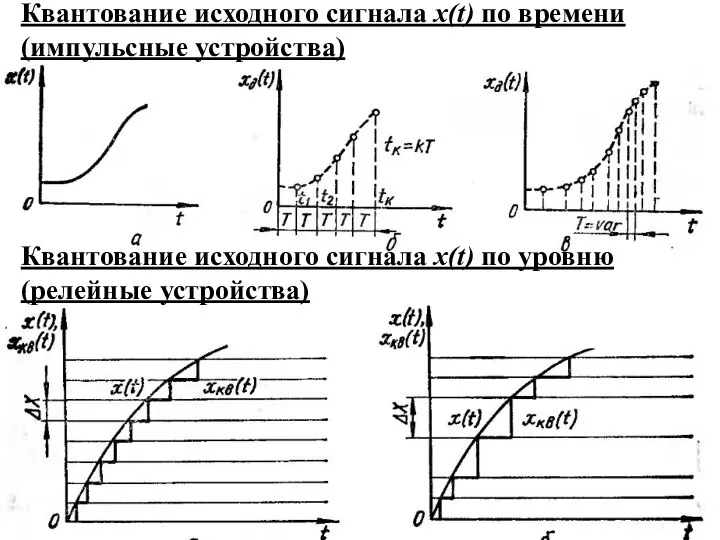
Слайд 8Квантование исходного сигнала х(t) по времени (импульсные устройства)
Квантование исходного сигнала х(t)
Квантование исходного сигнала х(t) по времени (импульсные устройства)
Квантование исходного сигнала х(t)
Слайд 9Цифровые электронные устройства (ЦЭУ) реализуют квантование исходного сигнала х(/) как по времени,
Цифровые электронные устройства (ЦЭУ) реализуют квантование исходного сигнала х(/) как по времени,

В свою очередь, конечному числу дискретных значений исходной физической величины можно поставить в соответствие некоторое число. Процесс замены дискретных уровней сигнала последовательностью чисел носит название кодирования, а совокупность полученных чисел называется кодом сигнала. Таким образом, процесс непосредственного преобразования и передачи сигналов можно заменить процессом преобразования и передачи кодов, поставленных в соответствие исходным сигналам.
Устройства, занимающиеся формированием, преобразованием и передачей кодов, поставленных в соответствие реальным значениям физических переменных, называют цифровыми устройствами. Передача кодов, каждый из которых, как правило, представляется некоторой последовательностью однотипных импульсов, требует некоторого времени. Очевидно, что это время больше времени, необходимого для передачи той же информации в импульсной и 1ем более непрерывной системах. Поэтому при прочих pamtux условиях количество информации, передаваемой цифровым способом, минимально.
Слайд 10Релейные электронные устройства (РЭУ) реализуют квантование исходного сигнала x(t) по уровню и
Релейные электронные устройства (РЭУ) реализуют квантование исходного сигнала x(t) по уровню и

Основная область применения РЭУ связана не с преобразованием информации, а с преобразованием энергии, т. е. с силовой электроникой По сравнению с ИЭУ они, как правило, проще (отсутствует импульсный модулятор) и обладают большим быстродействием.
Слайд 11Достоинства ЦЭУ: высокая помехоустойчивость; высокая на дежность; возможность длительного хранения информации без
Достоинства ЦЭУ: высокая помехоустойчивость; высокая на дежность; возможность длительного хранения информации без

Недостатки ЦЭУ: малое быстродействие; малая точность.
Однако меньшее быстродействие цифровых устройств с лихвой окупается возможностью унификации самих цифровых элементов, что позволяет с помощью их большого количества успешно решать вопросы повышения точности и быстродействия ЦЭУ.
Минимально возможный объем, который может занимать ЭУ, к конечном счете определяется количеством теплоты, выделяемой в этом объеме. Поэтому использование дискретных ^методов обработки информации позволяет реализовать ДЭУ в значительно меньшем объеме, чем в случае аналоговой информации.
Ранее мы отметили, что способность реализации сложных алгоритмов обработки информации в минимальных объемах с минимальными затратами и высокой надежностью работы является основной причиной повсеместного использования электронных >стройств Сказанному в полной мере отвечают цифровые электронные устройства, которые, несмотря на меньшие быстродействие и точность по сравнению с другими рассмотренными типами ЭУ, получают в настоящее время все большее распространение.
Слайд 12Цифровыми наз. устройства формирования, преобразования и передачи кодовых слов.
Кодом наз. систему символов
Цифровыми наз. устройства формирования, преобразования и передачи кодовых слов.
Кодом наз. систему символов

В цифровой технике для записи кодовых символов, или просто кода, используют две цифры: 0 и 1 (сигналы с двумя уровнями напряжения: высоким и низким).
Современные устройства цифровой обработки информации используют: числа и логические переменные.
Числа - количественные характеристике процесса, объекта, системы, над ними можно производить арифметические действия.
Логические переменные определяют состояние системы или принадлежность её к определённому классу состояний.
Преобразователи кодов служат для перевода одной формы бинарного числа (кодовой комбинации) в другую, например, преобразование двоично-десятичного кода в семисегментный код индикатора. Входные и выходные коды преобразователей связаны между собой. Эту связь задают логическими функциями или в виде таблицы переключений.
Слайд 13Цифровые методы передачи информации по сравнению с
другими имеют ряд преимуществ. Главными из
Цифровые методы передачи информации по сравнению с
другими имеют ряд преимуществ. Главными из

1) приём сигнала сводится не к измерению, а к обнаружению 1 или 0;
2) сообщения в цифровой форме легко обрабатываются, запоминаются,
коммутируются и регистрируются;
3) возможна многократная передача без накопления ошибок;
4) применение помехоустойчивого кодирования позволяет значительно
увеличить достоверность передачи телемеханических сообщений;
5) упрощаются требования, предъявляемые к радиолиниям в отношении калибровки эталонных уровней;
6) улучшается использование канала связи в случае применения специальных кодов, статистически согласованных с передаваемыми сообщениями.
Под кодированием в широком смысле понимается переход от одного
способа задания информации к другому, допускающий восстановление исход-
ной информации. Теория кодирования получила большое развитие, начиная с
40-х годов ХХ века после работ К.Шеннона.
В данном конспекте большое внимание уделено теоретическим основам
построения кодовых комбинаций, а также преобразованию кода передаваемой
и обрабатываемой информации с сохранением его числового эквивалента.
Преобразование может осуществляться программным или аппаратным способом.
Целями кодирования сообщений обычно являются:
1) передача по общему каналу связи нескольких или многих сообщений
для кодового разделения сигналов;
2) повышение помехоустойчивости и достоверности передачи сообщений;
3) более экономное использование полосы частот канала связи, т.е.
уменьшение избыточности;
4) уменьшение стоимости передачи и хранения сообщений;
5) обеспечение скрытности передачи и хранения информации;
6) преобразование любой информации независимо от ее происхождения и
назначения в единую систему символов;
7) приведение исходных символов в соответствие с характеристиками канала связи.
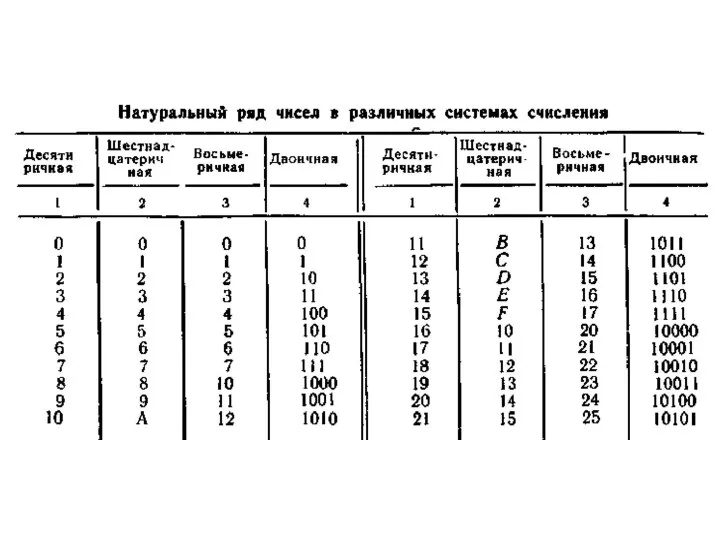
Слайд 14Существующие системы счисления подразделяются на позиционные и непозиционные. В непозиционных системах значение
Существующие системы счисления подразделяются на позиционные и непозиционные. В непозиционных системах значение

Число q наз. основанием системы счисления, может быть как целым, так и дробным. Если в выражении (14.1) отбросить весовые коэффициенты q' и соответствующие знаки сложения, то получим сокращенную запись числа, носящую название q-ичного кода числа Х„. Номер позиции цифры , называют его разрядом. Разряды с положительными степенями q образуют целую часть числа Хq, с отрицательными степенями — дробную. Цифры
соответственно являются старшим и младшим разрядами числа.
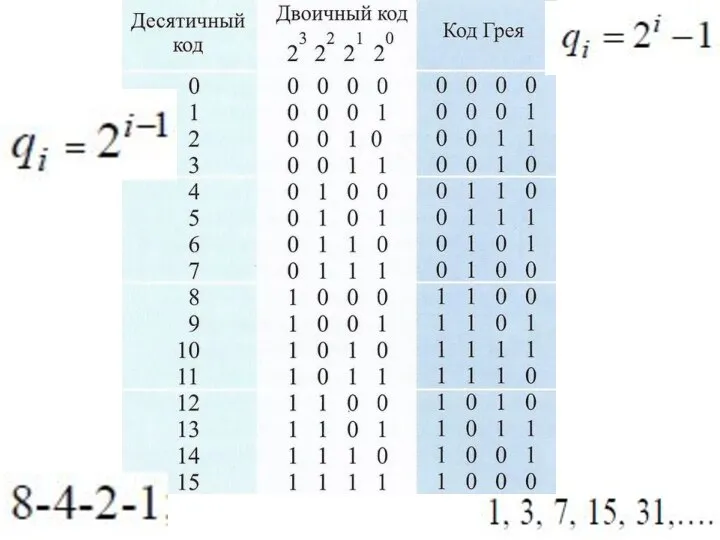
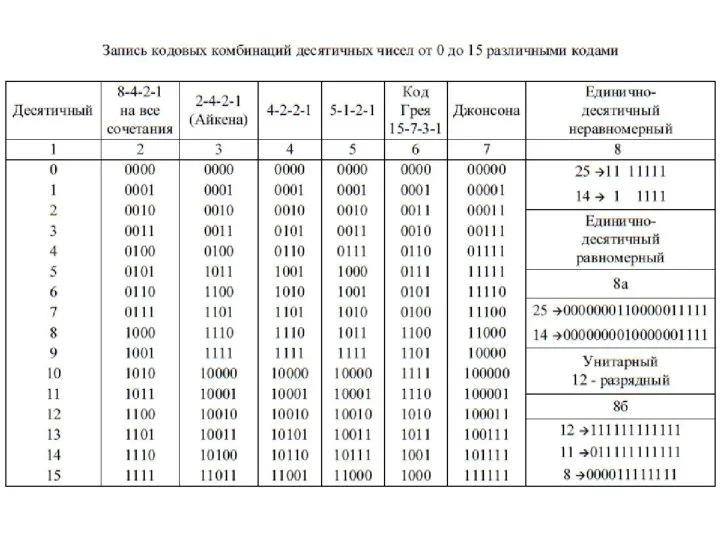
Слайд 15Количество различных чисел, которое может быть записано в позиционной системе счисления с
Количество различных чисел, которое может быть записано в позиционной системе счисления с

Количество разрядов, необходимое для записи в позиционной системе счисления с основанием q некоторого числа X, можно оп- ределить из следующих соображений. Для записи числа X в системе с основанием q должно выполняться условие
Тогда
В цифровой технике нашли применение только позиционные системы счисления.
Слайд 161110110011
1110110011

Слайд 17Число символов в кодовом слове цифрового устройства фиксировано, т.е. кодовые слова имеют
Число символов в кодовом слове цифрового устройства фиксировано, т.е. кодовые слова имеют

Если кодовое слово имеет п символов (разрядов), то из них можно составить N = 2n комбинаций кодовых слов. Например, в 32-разрядном вычислительном устройстве можно закодировать 232 = 4 296 967 298 слов.
Для оценки количества цифровой информации используют бит и байт (1 байт = 8 бит).
Функционирование цифровых устройств можно представить следующим образом:
посредством генератора тактовых импульсов производится синхронизация начала выполнения отдельных операций преобразования входного кодового слова и отводится время выполнения команды (в течение одного или нескольких периодов тактовых импульсов);
после активизации начала операции осуществляется преобразование всех входных кодовых слов (логических нулей и единиц) в требуемые выходные кодовые слова;
выходные кодовые слова отправляются на хранение в память цифрового устройства и/или во внешние устройства для выполнения определённых действий.
Слайд 18Переход от системы счисления с большим основанием к системе счисления с меньшим
Переход от системы счисления с большим основанием к системе счисления с меньшим

а) целая часть исходного числа делится на основание новой системы счисления;
б) дробная часть исходного числа умножается на основание новой системы счисления. Преобразуем число 25,12 в двоично-десятичную систему
Слайд 19В качестве математического аппарата для функций и аргументов, принимающих только два значения
В качестве математического аппарата для функций и аргументов, принимающих только два значения
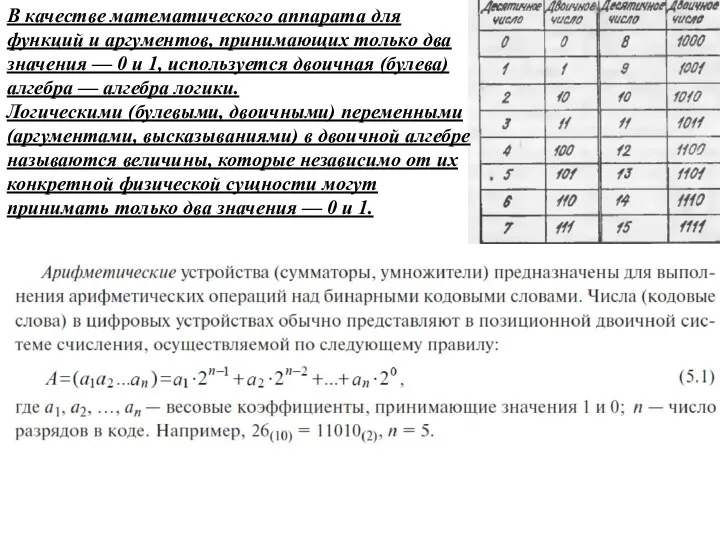
Логическими (булевыми, двоичными) переменными (аргументами, высказываниями) в двоичной алгебре называются величины, которые независимо от их конкретной физической сущности могут принимать только два значения — 0 и 1.
Слайд 23Самые современные и мощные микропроцессоры (компьютеры) из перечня арифметических операций способны выполнять
Самые современные и мощные микропроцессоры (компьютеры) из перечня арифметических операций способны выполнять

Основной арифметической операцией, которая используется в цифровой технике, является сложение двоичных чисел, а к нему приводятся другие — вычитание, умножение, деление.
Двоичные числа складываются так же, как и десятичные: 02 + 02 = 02; 02 + 12 = 1 2; 12+ 02 = 12; 12+12= 102. Для «удобства» ЦВМ, в последнем случае, записывается 0 от 10, а 1 оставляется в «уме машины» для переноса в первый разряд. Последнее сложение записывается и читается так: «1 + 1 = 0 плюс перенос 1». При сложении многоразрядных чисел эта перенесённая единица находит своё место. Вычитание
Положим, что из 10102 надо вычесть 01112, что равносильно 1010 — 710 =З10). Алгоритм вычисления таков: сначала двоичное вычитаемое число прямого кода [A]n = 01112 записывается в форме обратного кода [А]д = 10002 (в обратном коде все 1 прямого кода заменяются на 0, а 0 — на 1). Результат обратного кода складывается с уменьшаемым, то есть 10102 + [А]д = 10102 + 10002 =100102 и получают промежуточное число 100102. После этого производится перенос 1 из высшего разряда (отмечен жирным курсивом) промежуточного числа, и она складывается с содержимым младшего разряда, то есть 00102 + 12 = 00112. Заметив, что произведённый перенос 1 называется циклическим переносом, резюмируем, что полученное число 00112, равное З10, и есть искомый результат вычитания. Изложенный алгоритм вычитания не удобен для человека, однако, он «удобен» для ЦВМ.
Операции умножения и деления также приводятся к сложению
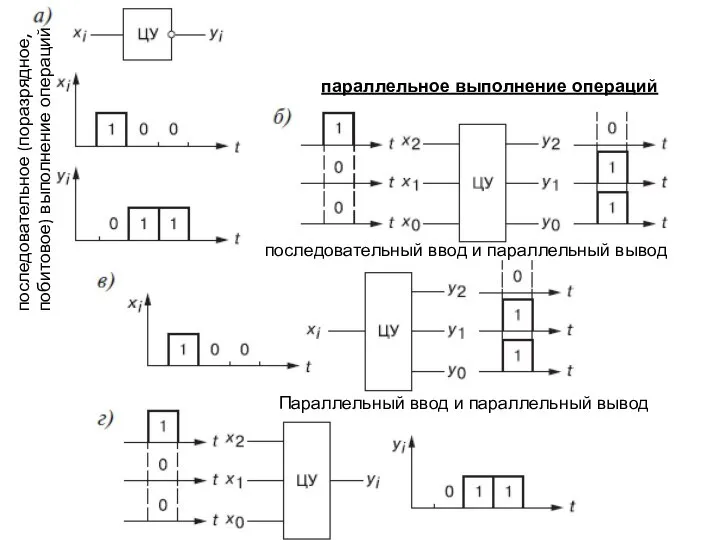
Слайд 24Операции над кодовыми словами, представленными в виде электрических сигналов, в цифровом устройстве
Операции над кодовыми словами, представленными в виде электрических сигналов, в цифровом устройстве

последовательное (поразрядное, побитовое) выполнение операций, при котором символы 1 и 0 кодового слова поступают последовательно по времени на единственный вход цифрового устройства и по завершении операции последовательно символ за символом выводятся из него. На рис. 5.1, а показано выполнение операции цифровым устройством ЦУ (инвертором) над трехразрядным входным словом х2х1х0 = 100, при котором биты выходного слова у2у1у0 = 011 принимают противоположные значения;
параллельное выполнение операций, при котором символы 1 и 0 кодового слова поступают одновременно на три входа ЦУ и по завершении операции одновременно выводятся из него (рис. 5.1, б).
В ряде случаев используют комбинированные способы обработки информации: с последовательным вводом и параллельным выводом (рис. 5.1, в) и с параллельным вводом и последовательным выводом (рис. 5.1, г)
Слайд 25последовательное (поразрядное, побитовое) выполнение операций
параллельное выполнение операций
последовательный ввод и параллельный вывод
Параллельный
последовательное (поразрядное, побитовое) выполнение операций
параллельное выполнение операций
последовательный ввод и параллельный вывод
Параллельный
Слайд 27Логический элемент ИЛИ моделирует операцию логического сложения, или, как ее еще называют,
Логический элемент ИЛИ моделирует операцию логического сложения, или, как ее еще называют,

А+В=С или А\/ В=С. Буквами А и В обозначены простые высказывания, или двоичные переменные, буквой С — сложное высказывание, или переключательная функция. Последнее название показывает, что функция зависит от переключений переменных А и В. Если простые высказывания соединены союзом «или», то сложное высказывание истинно, если истинно хотя бы одно из простых высказываний. Соответственно, С должно равняться 1, если А или В равны 1 по отдельности или одновременно. Зависимость между двоичными переменными А и В и переключательной функцией С может быть задана в виде таблицы истинности, в ней написаны условия истинности сложного высказывания в зависимости от истинности простых высказываний.
Слайд 28Логический элемент И выполняет операцию логического умножения, или конъюнкции. Алгебраически эта операция
Логический элемент И выполняет операцию логического умножения, или конъюнкции. Алгебраически эта операция
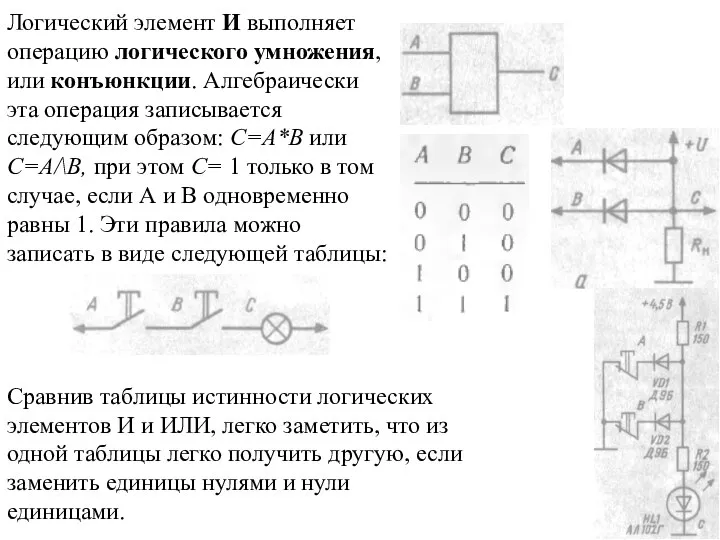
Сравнив таблицы истинности логических элементов И и ИЛИ, легко заметить, что из одной таблицы легко получить другую, если заменить единицы нулями и нули единицами.
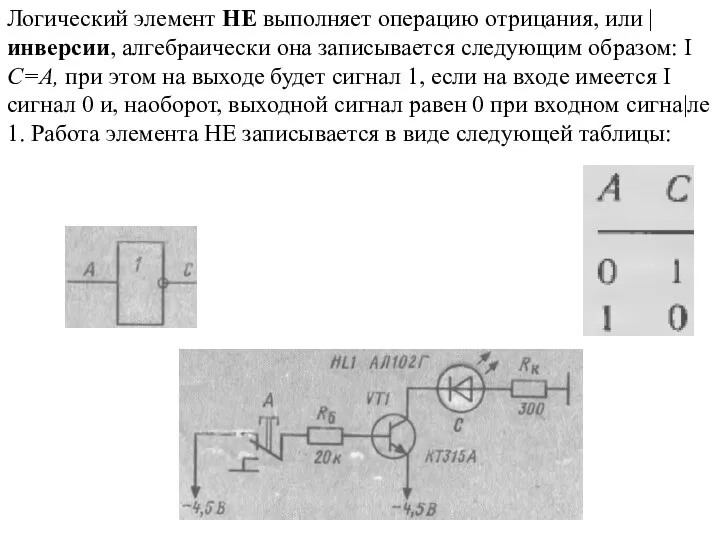
Слайд 29Логический элемент НЕ выполняет операцию отрицания, или | инверсии, алгебраически она записывается
Логический элемент НЕ выполняет операцию отрицания, или | инверсии, алгебраически она записывается
Слайд 30Функция "И" равна единице, если равны единице ВСЕ ее аргументы. Функция "ИЛИ"
Функция "И" равна единице, если равны единице ВСЕ ее аргументы. Функция "ИЛИ"

Есть мужчины (М) и женщины (Ж)
у МЖ и ЖМ могут быть дети,
у ММ и ЖЖ нет!
Для двух значений результатом исключающего или будет единица, если начальные значения разные, и ноль, если одинкаовые:
Слайд 31Булевые (переключательные) функции бывают комбинационными и временными.
Комбинационными наз. функции, значение которых однозначно
Булевые (переключательные) функции бывают комбинационными и временными.
Комбинационными наз. функции, значение которых однозначно

Схемы, реализующие комбинационные функции, называются комбинационными (КС).
Временными (функциями с памятью) наз. функции, значения которых определяются как значениями аргументов в данный момент времени, так и другими параметрами, прежде всего временем, поэтому при одних и тех же значениях аргументов значение временной функции может быть разным.
Временные функции делят на:
-- временные булевы функции (ВБФ) типа
Значение этой функции при одних и тех же значениях аргументов зависит от момента времени, т. е. в различные моменты времени реализуются различные комбинационные булевы функции;
-- рекуррентные булевы функции первого рода (РБФ-1) типа
--рекуррентные булевы функции второго рода (РБФ-2) типа

 "Взаимодействие семьи и школы в воспитании ребенка"
"Взаимодействие семьи и школы в воспитании ребенка" Взаимодействие органов внутренних дел на воздушном и водном транспорте с территориальными ОВД
Взаимодействие органов внутренних дел на воздушном и водном транспорте с территориальными ОВД Сумматоры
Сумматоры Рущенко Н.Н
Рущенко Н.Н МОРС
МОРС Право на службе человека
Право на службе человека Презентация на тему История микроскопа
Презентация на тему История микроскопа  Ажурное яичко
Ажурное яичко Качественные методы исследований
Качественные методы исследований В.В. Кандинский — российский отец мирового абстракционизма
В.В. Кандинский — российский отец мирового абстракционизма Как продаются товары потребителям
Как продаются товары потребителям Произведения К.И.Чуковского
Произведения К.И.Чуковского Презентация на тему Имею право
Презентация на тему Имею право ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНЫХ ТРЕНАЖЕРОВ ДЛЯ РАЗВИТИЯ СЛУХОРЕЧЕВОЙ ФУНКЦИИ У ДЕТЕЙ И ВЗРОСЛЫХ С НАРУШЕНИЕМ СЛУХА
ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНЫХ ТРЕНАЖЕРОВ ДЛЯ РАЗВИТИЯ СЛУХОРЕЧЕВОЙ ФУНКЦИИ У ДЕТЕЙ И ВЗРОСЛЫХ С НАРУШЕНИЕМ СЛУХА Интерференция света
Интерференция света  Organizatsia_Obedinennykh_Natsiy
Organizatsia_Obedinennykh_Natsiy Единая Справочная Служба
Единая Справочная Служба Магический реализм Рэя Брэдбери в повести «Канун всех святых» («The Halloween Tree»)
Магический реализм Рэя Брэдбери в повести «Канун всех святых» («The Halloween Tree») Средства массовой информации и анализ информационных программ
Средства массовой информации и анализ информационных программ Географическое положение и история исследования Австралии
Географическое положение и история исследования Австралии Ялуторовский фермер
Ялуторовский фермер Что такое спортивное ориенирование
Что такое спортивное ориенирование Библия. Книга книг
Библия. Книга книг Экспериментальная установка теплового насоса
Экспериментальная установка теплового насоса БЭК-ОФИС СОЗДАНИЕ, РАЗВИТИЕ, АВТОМАТИЗАЦИЯ
БЭК-ОФИС СОЗДАНИЕ, РАЗВИТИЕ, АВТОМАТИЗАЦИЯ Презентация на тему Правила для пешеходов
Презентация на тему Правила для пешеходов  Вовлечение молодёжи в здоровый образ жизни и занятия спортом
Вовлечение молодёжи в здоровый образ жизни и занятия спортом Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint